Matematizziamo il nastro di Möbius ,parte 12°: il Piano proiettivo .****
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Proseguiamo con le nostre superfici generate in modo astratto, tramite la topologia quoziente. Vogliamo costruire un nuovo spazio topologico, il piano proiettivo, tramite le nostre identificazioni di punti. Ma ricordiamoci prima la definizione "canonica" di piano proiettivo , che è la seguente:
Consideriamo l'insieme , ovvero l'insieme dei punti dello spazio tridimensionale individuati da terne (x1,x2,x3) di numeri reali ,privato dello 0. Consideriamo in tale insieme la relazione di equivalenza così definita:
se e solo se esiste
tale che
, ossia, scritto per esteso:
.
Tale relazione è riflessiva:
x=1*x
simmetrica:
se esiste tale che
, allora
transitiva:
se allora
; se
allora
quindi
, e posto
sia ha
che implica
.
Quindi è una relazione di equivalenza. Lo spazio quoziente
è pertanto un spazio topologico, si chiama piano proiettivo reale, e si indica con
.
Poichè i vettori appartenenti a una stessa retta vengono identificati tra loro, può essere identificato con l’insieme delle direzioni, ovvero come l’insieme delle rette di
passanti per l’origine.
Lo spazio proiettivo è di Hausdorff ; per una volta credetemi sulla parola, in quanto non siamo ancora in grado di dimostralo (ricordo che uno spazio topologico è di Hausdorff se punti distinti ammettono intorni disgiunti. Tale tipo di spazio si dice anche separato).
Un altro modo di generare il piano proiettivo consiste nel utilizzare la sfera unitaria () e considerare equivalenti i punti della superficie che sono antipodali, ossia p ∼ −p. Intuitivamente , per definire tutte le direzioni non serve l'intero spazio
, ma bastano i punti della superficie sferica, a patto di identificare i punti antipodali come lo stesso punto in quanto le due rette passanti per essi e per l'origine coincidono, ed individuano pertanto la stessa direzione, ovvero lo stesso punto di
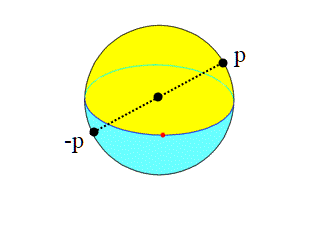
La proiezione , ha come immagine il piano proiettivo; essendo la sfera
compatta anche
essendo l'immagine tramite la funzione continua
della sfera risulta compatto.
Un altro modo per costruire il piano proiettivo è il seguente:
Consideriamo nel piano il disco unitario
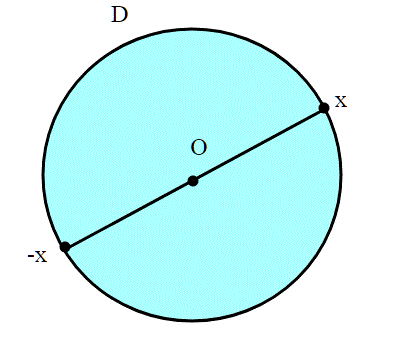
In esso, definiamo una relazione di equivalenza dove i punti interni corrispondono a se stessi, mentre un punto x sul bordo ha un solo punto equivalente, che è il simmetrico di x rispetto al centro,ovvero . Come nella sfera, lo spazio quoziente genera lo stesso spazio topologico
, o meglio due spazi topologici omeomorfi. Ma dimostrare questo non è immediato. Possiamo comunque provarci. Ma andiamo per gradi.
Richiami sulle funzioni quoziente
In questo articolo abbiamo trattato le funzioni quoziente. Penso sia meglio riprendere un attimo il discorso prima di continuare. Dati i tre spazi topologici X,Y,Z:
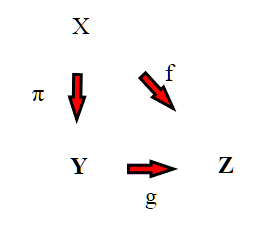
dove X è uno spazio topologico, Y lo spazio quoziente, rispetto ad una certa relazione d'equivalenza e Z uno spazio topologico.
il nostro problema era costruire un omeomorfismo che va da Y--->Z.
Sappiamo che se esiste una f: X-->Z continua, tale che assuma gli stessi valori su punti equivalenti, simbolicamente:
*
allora definendo g([p])=f(p) sappiamo che la definizione di g è ben posta, ossia non dipende dal rappresentante della classe. Ci viene adesso in aiuto un noto teorema di topologia (chiamato Proprietà universale del quoziente), che ci assicura che g:Y--->Z è continua se e solo se la composizione è continua.
Vogliamo adesso estendere questo tipo di ragionamento a due spazi quoziente. Siano A,B due spazi topologici e su ciascuno di essi sia definita una relazione di equivalenza.Per non complicare la notazione, pur commettendo un abuso, scriveremo in luogo di
. Pertanto la relazione verrà identificata dall' insieme in cui viene considerata.
Vogliamo risolvere il seguente problema: trovare una funzione continua g fra i due quozienti:
. Ricordo che con [p] indichiamo la classe degli elementi equivalenti a p, ovvero l'elemento dell'insieme quoziente rappresentato da p.
Supponiamo che esista una funzione f: A--->B, continua, che soddisfi la seguente proprietà:
**
ovvero che mandi punti equivalenti in punti equivalenti. Consideriamo il seguente diagramma:
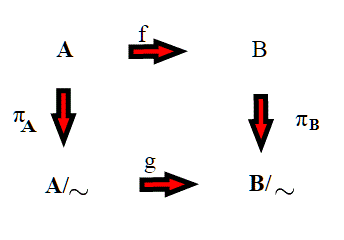
Definiamo g come g([p])=[f(p)]. Valendo **, la definizione è ben posta.
si ha che ; infatti se
,
.
è continua, essendo la composizione di due funzioni continue. Ma allora anche
è continua, vista l'eguaglianza. Siamo allora nelle condizioni della Proprietà universale del quoziente:
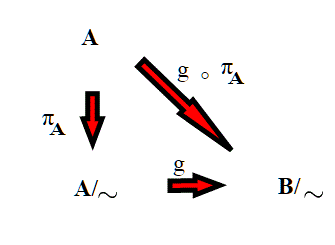
Quindi anche g è continua. 1)
Siamo adesso in grado di dimostrare che i due spazi quoziente, uno costruito sul disco e l'altro dalla sfera sono omeomorfi e rappresentano quindi lo stesso spazio,il piano proiettivo.
Per far ciò, costruiamo una funzione che sia compatibile con le due relazioni di equivalenza definite su disco e sfera.
questa funzione manda il disco nell’ emisfero superiore della sfera.
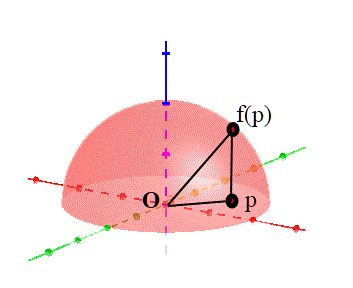
La funzione f è continua, in quanto le sue tre componenti sono continue.
La f soddisfa la proprietà **:
** ;
se infatti sul disco prendiamo due punti equivalenti, o sono uguali (se sono interni) oppure sono sul bordo del disco. Sia (s,t) un tale punto, per esso vale l'eguaglianza . Ma allora:
f(−x) = f(−s,−t) = (−s,−t, 0) = −f(x)
=f(-x) che è proprio la proprietà **. La funzione g definita come g([p])=[f(p)] che va da :
è quindi continua, per quanto visto in 1).Per dimostrare che g è suriettiva è sufficiente osservare ogni classe di equivalenza in
ha almeno un rappresentante nell’ immagine di f, e questo è vero, infatti dato un punto p della sfera almeno uno dei punti p e −p è contenuto nell'emisfero superiore (cioè nell' immagine di f).
La mappa quoziente g è iniettiva se e solo se f soddisfa . (in una direzione l'abbiamo già visto, nell'altra è quasi banale) Se ci ricordiamo ora del nostro teorema "necessario" :
Sia f : X -->Y un’applicazione continua e biunivoca. Se X è compatto e Y è di Hausdorff allora è un omeomorfismo.
Possiamo quindi concludere che g è un omeomorfismo.
Un terzo modo per costruire il piano proiettivo.
Un altro modo classico per costruire il piano proiettivo è considerare il quadrato [0,1] x [0,1]: questa volta incolliamo (identifichiamo) i lati in questo modo:
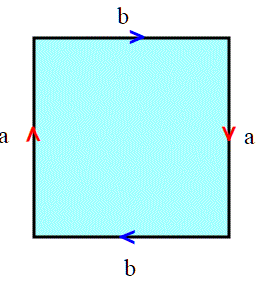
che corrisponde a considerare equivalenti i punti del bordo del quadrato in questo modo:
(0, t) ∼ (1, 1 − t) e (s, 0) ∼ (1 − s, 1). Al solito i punti interni del quadrato sono equivalenti solo a se stessi. Lo spazio quoziente rispetto a questa relazione di equivalenza è ancora lo spazio proiettivo. Perchè? ricordiamoci che il quadrato è omeomorfo al cerchio, lo abbiamo visto in uno dei primi articoli de questa serie:

l'omeomorfismo è semplicemente quello della figura,che associa ad un punto del quadrato il punto della circonferenza che si trova nell'intersezione col segmento OX che congiunge il punto X con il centro della circonferenza. Ma torniamo adesso al nostro schema di identificazione dei lati, e condensiamo tutto in un unico disegno, dove mettiamo anche il disco con la relazione antipodale.
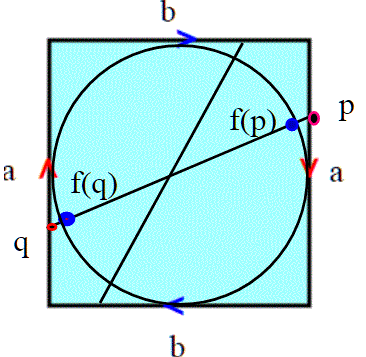
Chiamiamo Q il quadrato e D il disco; vogliamo dimostrare che il quoziente del quadrato è omeomorfo al quoziente del disco con la relazione antipodale. Sia f funzione descritta nei due disegni sopra; f è un omeomorfismo, quindi è continua. Come si vede dal disegno **. Ci troviamo con un discorso analogo a quello visto sopra nel caso di sfera e disco; se definiamo g([p])=[f(p)] avremo un omeomorfismo g fra:
g: ; quindi anche con la relazione definita sul quadrato il quoziente topologico è il piano proiettivo.
Il piano proiettivo è una superficie chiusa non orientabile
Analogamente a quanto visto per la bottiglia di Klein, lo spazio proiettivo essendo compatto e privo di bordi, è una superficie chiusa. Abbiamo poi appena visto che il piano proiettivo si può definire con la relazione di equivalenza definita dallo schema:

analogamente a quanto fatto per la bottiglia di Klein, notiamo graficamente che il piano proiettivo contiene un nastro di MÖBIUS (il rettangolo azzurro):
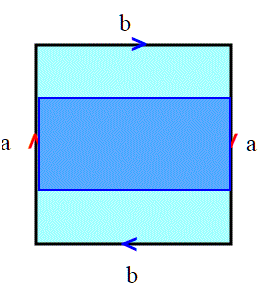
pertanto il piano proiettivo è una superficie chiusa non orientabile.
Piano proiettivo e spazio quadridimensionale.
Non esiste un omeomorfismo del piano proiettivo in una superficie dello spazio tridimensionale , ma esiste invece nello spazio di dimensione 4. Riprendiamo in mano la sfera immersa nello spazio tridimensionale. Sappiamo che se su di essa consideriamo la relazione antipodale, il quoziente
rappresenta proprio lo spazio proiettivo
. Consideriamo ora la funzione
definita da:
la funzione f assume gli stessi valori su punti equivalenti della sfera. Infatti come si verifica banalmente. Pertanto possiamo definire una funzione
data da: g([p])=f(p) , essendo indipendente dal rappresentante della classe [p]
g è continua e chiaramente suriettiva su ; g è anche iniettiva, quindi possiamo concludere ,in base al teorema "necessario" , che è proprio un omemomorfismo di
, quindi anche di
.
Le superfici rappresentative di nello spazio tridimensionale.
Non possiamo trovare una superficie omeomorfa al piano proiettivo nello spazio tridimensionale. Esistono però delle superfici che rappresentano il piano proiettivo avendo però delle autointersezioni. Le presentiamo così, solo graficamente, per dare una idea della complessità e della bellezza del piano proiettivo. Una di queste è la superficie di Steiner, detta anche superficie romana.
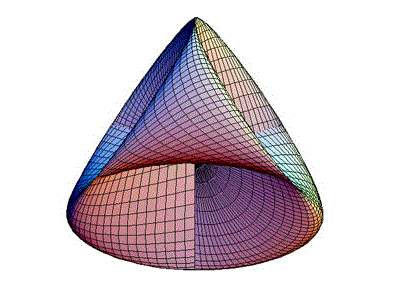
Un'altra rappresentazione del piano proiettivo è data dalla superficie di Boy , che fu allievo di Hilbert:
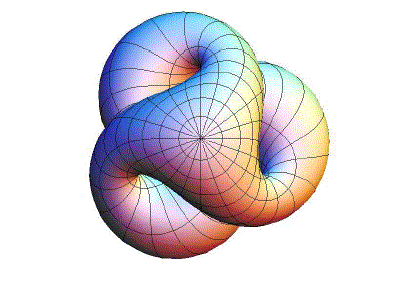






2 commenti
Caro Umberto, giustamente parli di bellezza, concludendo questo dodicesimo articolo dedicato alla topologia.
Come non si può restare ammirati davanti a quelle due ultime figure? Ma oltre alla loro rilevanza estetica la bellezza sta anche nel pensiero che le ha generate, nel loro intrinseco significato matematico.
Complimenti per questa serie di articoli che ci accompagna alla scoperta di queste meraviglie.
grazie. Penso seguirà un appendice almeno sulla superficie di Steiner. É troppo importante.Come dici quell immagine nasce più dal pensiero matematico che dal calcolatore.