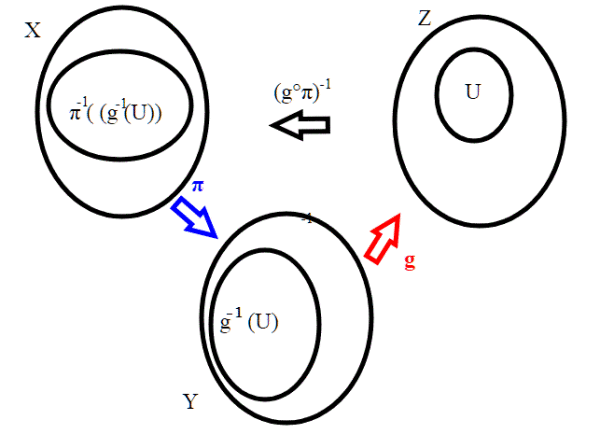
Le funzioni quoziente ****
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Riprendiamo ancora una volta l'esempio del segmento di cui incolliamo gli estremi. Chiaramente l'incollamento avviene con l'identificazione di punti, tramite la topologia quoziente.
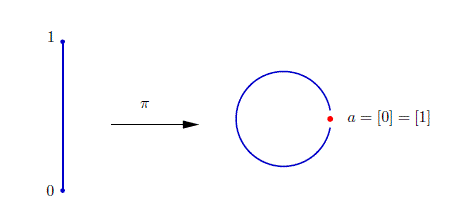
Sia X=[0,1]. Consideriamo la relazione di equivalenza in cui tutti i punti interni al segmento sono equivalenti solo a se stessi,mentre per i punti estremi . Sappiamo che lo spazio quoziente, che indichiamo con
, è uno spazio topologico. X è un sottoinsieme di R (fra l'altro compatto, come abbiamo visto nell'ultimo articolo), ma nulla sappiamo su
a parte il fatto che sia uno spazio topologico. Chi vuole ricordare meglio la topologia quoziente , può guardare qui.
Ci troviamo per ora in questa situazione; è la proiezione che ad ogni elemento di X associa la sua classe di equivalenza.
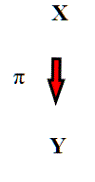
Y è quello che si definisce astrattamente un cerchio, grazie alla nostra intuizione. Però per noi il cerchio Euclideo è un'altra cosa; Lo possiamo descrivere analiticamente in con una funzione parametrica che usa le funzioni trigonometriche, definita sempre su X=[0,1].
Sia dunque f:[0,1] definita da:
f(t) = (cos 2πt, sin 2πt). Questa applicazione rappresenta un cerchio di raggio unitario nel piano Euclideo Infatti la somma dei quadrati delle due coordinate vale 1, qualsiasi sia t.

Questo è proprio il cerchio che noi conosciamo. Dunque f: [0,1]---> Z, dove , cerchio unitario. Il problema che vogliamo risolvere è il seguente; trovare una funzione g: Y-->Z, ovvero fra il cerchio definito in modo astratto tramite il quoziente, e il cerchio vero e proprio. Se riusciamo a trovare questa g, che sia inoltre continua e invertibile, avremmo un omeomorfismo fra i nostri due spazi, che ci farebbe concludere che topologicamente sono la stessa cosa. Possiamo definire la g tramite la funzione f. Questo ad un patto; che la funzione f assuma gli stessi valori su punti equivalenti. Simbolicamente:
*. Infatti, se questo è vero, la funzione g è ben definita, ovvero non nasce ambiguità. g viene infatti applicata agli elementi dell'insieme quoziente, le classi [p]. Se [p]=[q], ovvero se cambiamo rappresentante per la classe, il valore non cambia, essendo g([p])=g[q])=f(p)=f(q). Siamo allora in grado di chiudere il seguente diagramma, e trovare la funzione g:
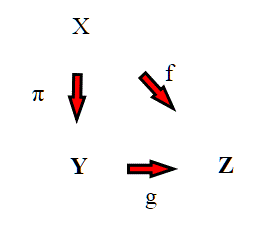
Nel nostro esempio si ha allora che f(0)=(cos0,sin0)=(1,0)=cos2π, sin2π)=(1,0). Dunque f soddisfa alla *. Possiamo allora definire g:
con g([p])=f(p). g è continua? Ci viene adesso in aiuto un noto teorema di topologia (chiamato Proprietà universale del quoziente), che ci assicura che g:Y--->Z è continua se e solo se la composizione
è continua. La dimostrazione non è tanto difficile, ma esula un po' dalla nostra trattazione divulgativa.Per chi vuole approfondire:
Essendo f continua, per la proprietà universale del quoziente anche g è continua. La funzione g è poi anche iniettiva; infatti g([p]) = g([q]) si verifica se solo se f(p) = f(q), che vale se e solo se p = q oppure {p, q} = {0, 1}, ovvero se e solo se [p] = [q]. Ma allora adesso possiamo applicare il "Teorema necessario" dell' articolo che trovate qui:
Sia g : Y -->Z un’applicazione continua e biunivoca. Se Y è compatto e Z è di Hausdorff allora g è un omeomorfismo.
(ho sostituito il simbolismo di spazi e funzioni nell'enunciato del Teorema, per evitare confusioni)
La nostra g è continua e biunivoca; X=[0,1] è compatto, quindi anche la sua immagine Y lo è, essendo continua, mentre il cerchio
,sottospazio di
che è di Hausdorff, è anch'esso di Hausdorff. Quindi g è un omeomorfismo. Alla fine, abbiamo dimostrato la nostra intuizione; il "cerchio" costruito astrattamente con la topologia quoziente incollando gli estremi di un segmento, è omeomorfo ad un cerchio vero e proprio. Solo adesso possiamo capire l'importanza del "teorema necessario".
NOTA: questo spazio quoziente non è solo omemorfo ad un cerchio, ma anche a qualsiasi curva chiusa semplice, ovvero che sia continua e definita su [0,1] e faccia coincidere solo i punti 0,1.
Le funzioni tipo f, ovvero che soddisfano la proprietà:
, si chiamano funzioni che discendono dal quoziente, mentre le funzioni g che da esse derivano si chiamano funzioni quoziente.