Categorie: Fisica Fisica classica
Tags: attrito fisica fisica classica Newton sistema di riferimento inerziale
Scritto da: Arturo Lorenzo
Commenti:2
Soluzione generale Newtoniana al quiz su cuneo e cubo
Soluzione generale Newtoniana
Nella soluzione generale che espongo di seguito è stata considerata la situazione illustrata nel quiz ma con l'aggiunta di una forza esterna F, da considerarsi dato del problema, di direzione orizzontale e che agisce da sinistra verso destra sul cuneo.
Sia SRI il sistema di riferimento inerziale solidale al piano di scorrimento del cuneo. Sia SRN il sistema di riferimento solidale al cuneo, che quindi non è inerziale perché soggetto alla stessa accelerazione con cui si sposta il cuneo.
Poniamoci in SRI e consideriamo le forze agenti sul cuneo. Abbiamo :
- la forza peso, diretta verso il basso e perpendicolare al piano di scorrimento;
- la forza esterna F diretta orizzontalmente e da sinistra verso destra;
- la reazione R esercitata dal piano di scorrimento sulla faccia inferiore del cuneo. Tale reazione, considerato nullo il coefficiente di attrito, è diretta perpendicolarmente al piano di scorrimento
- l'azione N esercitata dal cubo sul cuneo. Poiché si è considerato nullo anche il coefficiente di attrito del piano di scivolamento del cubo sul cuneo, tale azione N è diretta perpendicolarmente a tale piano di scivolamento
Stabiliamo prima di tutto il significato dei simboli che verranno utilizzati seguito, oltre a quelli già introdotti sopra:
= vettore accelerazione orizzontale del cuneo nel sistema di riferimento inerziale (SRI)
= vettore accelerazione del cubo nel sistema solidale al cuneo (SRN), parallelo al piano di scivolamento
e
= componenti orizzontale e verticale di
= angolo di inclinazione del piano di scivolamento
Andiamo ora a scrivere l'equazione che traduce in formula la seconda legge della dinamica (F=m*a) per il cuneo lungo le due direzioni x e y del sistema di assi cartesiani considerato (asse x orizzontale e asse y verticale) . Consideriamo positivo il verso delle x da destra verso sinistra e quello delle y dall'alto verso il basso. Facciamo riferimento alla seguente figura.
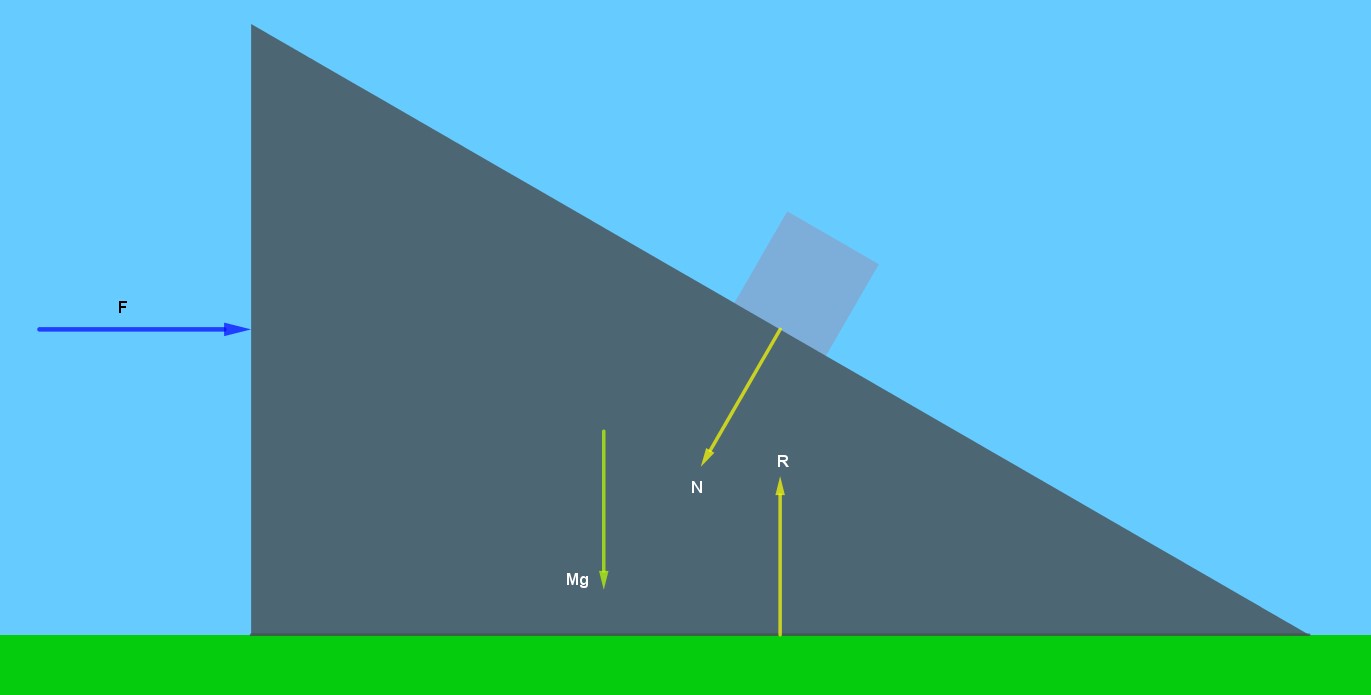
Lungo l'asse x avremo:
(1)
Lungo l'asse y, invece, avremo:
(2)
Infatti, il cuneo si sposta solo orizzontalmente, quindi la sua accelerazione lungo la verticale è nulla.
Ora spostiamo la nostra attenzione sul cubo, ma ponendoci in SRN. Stavolta, quindi, siamo solidali al cuneo , che si sposta orizzontalmente con accelerazione . Osservando il cubo da questi sistema di riferimento (non inerziale), vedremo agire su di esso:
- la forza peso mg , diretta verso il basso e perpendicolare al piano di scorrimento del cuneo;
- l'azione N esercitata dal cuneo sul cubo. E' la stessa vista prima nel caso del cuneo, quindi sempre diretta perpendicolarmente al piano di scivolamento del cubo.
- una forza apparente Fa dovuta al fatto che il sistema di riferimento da cui osserviamo il cubo si sposta con accelerazione orizzontale
. Tale forza apparente sarà , dunque, pari a m
Per convincerci della necessità di Fa, basta un po' di immaginazione. Pensiamo di essere in un'automobile e di osservare un oggetto sul cruscotto. Ipotizziamo trascurabile l'attrito tra oggetto e cruscotto. Quando il moto dell'automobile è rettilineo uniforme, l'oggetto sul cruscotto ci appare immobile . Se ora l'automobile accelera cosa succede ? L'oggetto inizia a muoversi sul cruscotto in verso opposto a quello dell'accelerazione. Se non avvertissimo in qualche modo la sensazione fisica dell'accelerazione sul nostro corpo e se non potessimo vedere nulla all'esterno dell'abitacolo, standoci dentro, per giustificare il moto dell'oggetto sul cruscotto dovremmo invocare la presenza di una forza. E' proprio quella la nostra Fa, con la differenza che al posto dell'automobile abbiamo il cuneo e che al posto dell'oggetto sul cruscotto c'è il cubo sul piano inclinato del cuneo. E' vero che in questo caso anche con cuneo (auto) fermo , il cubo (oggetto sul cruscotto) si muoverebbe scivolando verso il basso, ma, in presenza di una forza Fa, lo vedremmo scivolare più velocemente del previsto.
Andiamo allora a scrivere l'equazione che traduce in formula la legge di Netwon (F=m*a) anche per il cubo, stavolta lungo le due direzioni x' e y' di un sistema di assi cartesiani che ha l'asse x' parallelo al piano di scivolamento e l'asse y' perpendicolare all'asse x' e diretto verso l'alto. Consideriamo positivo il verso delle x' dall'alto verso il basso e quello delle y' dal basso verso l'alto. Facciamo riferimento alla seguente figura.
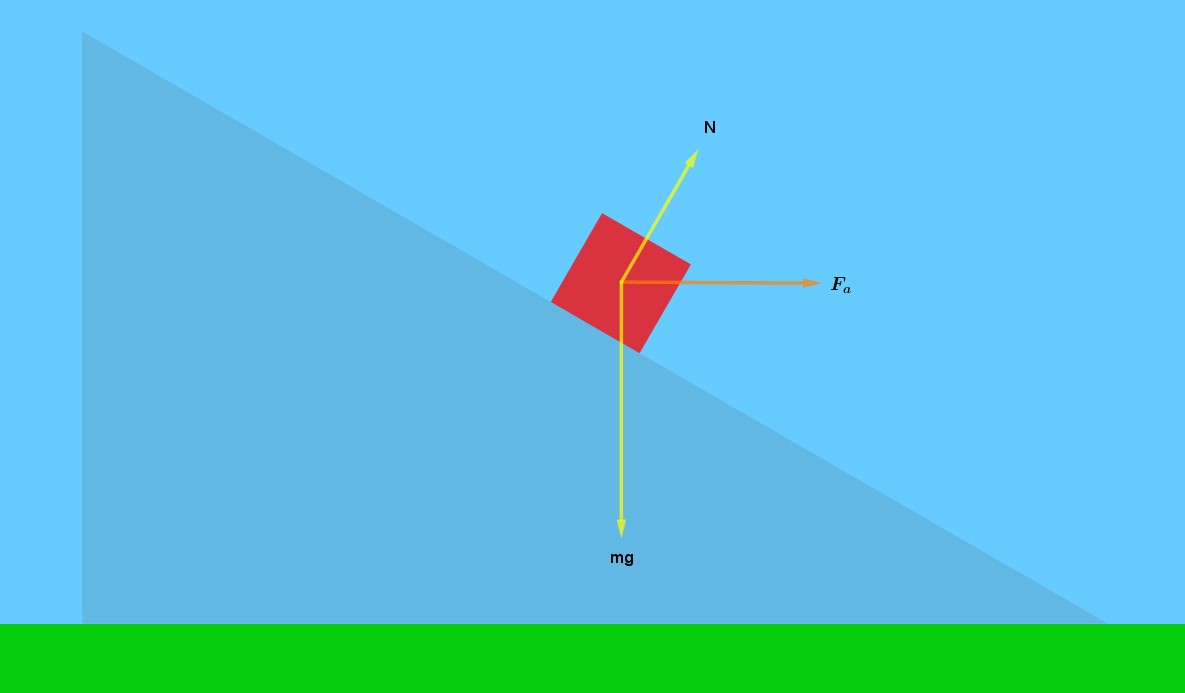
Lungo l'asse x' avremo:
cioè:
che, dividendo tutto per m, diventa:
(3)
Lungo l'asse y', invece, avremo:
cioè:
(4)
Abbiamo, dunque, un sistema di 4 equazioni , le (1), (2), (3) e (4), nelle 4 incognite N, R, e
. Risolvendolo, per esempio per sostituzione, si ottiene:
(5) (azione tra cuneo e cubo)
(6) (reazione sul cuneo da parte del piano di scorrimento)
(7) (accelerazione del cuneo rispetto all'osservatore solidale a SRI)
(8) (accelerazione del cubo in SRN, parallela al piano di scivolamento)
Possiamo scomporre la lungo gli assi x e y (asse x orizzontale e asse y verticale):
(9)
(10)
Calcoliamo ora la componente di lungo x nel sistema di riferimento inerziale SRI sottraendo alla
della (9) l'accelerazione del cuneo
, cioè:
(11)
La componente dell'accelerazione del cubo lungo y, invece, non cambia , passando da SRN a SRI, perché la forza apparente Fa è diretta orizzontalmente, quindi non ha componente lungo l'asse y. Sarà, quindi:
(12)
Tramite la (11), andando a sostituire le espressioni date dalla (9) e dalla (7) , si ottiene:
cioé:
(13)
Conoscendo, così, le due componenti dell'accelerazione del cubo in SRI, possiamo calcolare l'angolo di inclinazione della sua direzione:
con valori di e
dati dalle (13) e (10).
Dalle suddette formule si possono fare delle considerazioni su casi particolari.
Per esempio, prendiamo la (7), ossia la formula che ci restituisce l'accelerazione del cuneo in SRI. Ci chiediamo: si può verificare il caso in cui il cuneo non si muove affatto ? Basta imporre, nella (7) che l'accelerazione sia nulla Se è nullo il primo membro, ovviamente dovrà esserlo anche il secondo, quindi:
Una frazione si annulla se si annulla il numeratore, quindi:
cioè:
(14)
Quindi , quando la forza esterna F applicata al cuneo attinge un valore dato dalla (14), il cuneo rimane fermo !
Passando, invece, ad interessarci del cubo, prendiamo in considerazione la (8). Ci chiediamo: possono esserci casi in cui il cubo non scivola lungo il cuneo ? Ciò significa accelerazione del cubo in SRN nulla. Anche qui, poniamo a zero il secondo membro della (8):
Dunque:
da cui, infine:
(15)
Quindi, quando la forza esterna F applicata al cuneo attinge un valore dato dalla (15), il cubo resterà immobile rispetto al piano di scivolamento ! Vedremo, cioè, spostarsi il cuneo solo orizzontalmente, insieme al cuneo e fermo rispetto a quest'ultimo.
E se, invece, la forza esterna F avesse un valore maggiore di quello dato dalla (15), cosa succederebbe al cuneo ? In formule, questo caso si tradurrebbe nella disequazione (basta partire dalla (15) e andar a ritroso:
cioè, dalla (8):
Avendo stabilito all'inizio che il verso positivo per l'accelerazione del cubo in SRN era quello dall'alto verso il basso, dalla suddetta disequazione si deduce che in tal caso l'accelerazione del cubo in SI ha verso dal basso verso l'alto. Cioè, il cubo , anziché scivolare verso il basso, sale verso l'alto !
Ho implementato le formule sin qui ricavate in un modello realizzato con geogebra. Attraverso l'applicazione è possibile, utilizzando gli appositi cursori, variare il valore di m, M, ed F, visualizzando poi i risultati conseguenti, sia come valori sia visivamente facendo partire l'animazione con l'apposito pulsante START.
L'applicazione è raggiungibile al seguente link: app geogebra
QUI le altre soluzioni









2 commenti
La scelta di collegare la "demo" di Geogebra con il nostro Blog ha una valenza migliaia di volte superiore al suo opposto e la trovo GENIALE.
Essendo fruitore di Geogebra ho subito scelto di "seguire" Arturo Lorenzo anche li dove ho scoperto l'intelligente suggerimento: Se desideri approfondire Ecc..
Io l'articolo lo avevo ovviamente già letto sul blog ma, vi assicuro, che attraverso analoghe dimostrazioni di quiz o altro, il blog avrebbe una impennata di collegamenti e, come dice il saggio...Chi Assaggia ...Ritorna.
Questa è anche un MINIMA ...MINIMA... risposta al grido di dolore di Enzo sulla "diffusione del verbo"
Grazie Giorgio.
Sinceramente ho scoperto da poco che si possono aggiungere all'interno di una applicazione con geogebra riferimenti a pagine web esterne (links) in modo che chi ci fa click sopra viene catapultato sulla pagina web (nel nostro caso il Circolo). Sicuramente li aggiungerò anche alle prossime applicazioni.
Geogebra è davvero un bel programma , tra l'altro completamente gratuito, lo usano anche in diverse scuole superiori e , ho saputo, addirittura scuole medie. Anche se concepito per la geometria , nel piano e nello spazio, lo si può piegare anche ad utilizzi per la Fisica, come in questo caso.
Da poco gli sviluppatori hanno aggiunto anche per i dispositivi Android (prima era solo per quelli con iOS) la possibilità di vedere in realtà aumentata le "creature" geometriche realizzate con il software: per dire, ecco una bottiglia di Klein in bella mostra sulla mia scrivania, ripresa con lo smartphone....
(scusate la divagazione)