Categorie: Fisica classica Matematica
Tags: diamante formica viola quiz scoglio Teoria
Scritto da: Vincenzo Zappalà
Commenti:32
Lo scoglio del diamante **(*)
Una leggenda cosmica che ci permette di risolvere un bel problema di fisica e matematica. Pochi calcoli e un risultato decisamente interessante. L'asterisco in più vale per chi volesse DIMOSTRARE la conclusione.
La leggenda ci serve solo per introdurre la problematica da affrontare e il caso scelto può facilmente essere generalizzato.
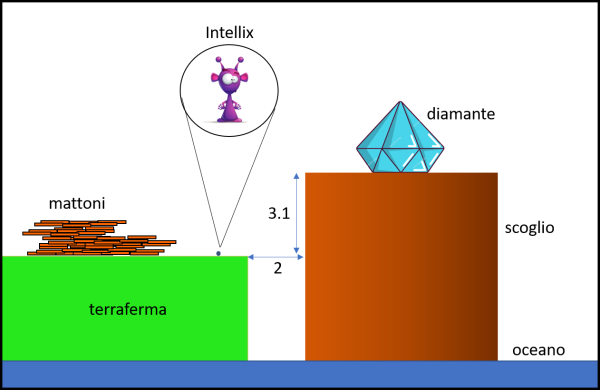
Nell'immensità del Cosmo esiste un pianeta veramente speciale, chiamato TEORIA. E' un mondo veramente straordinario in quanto su di esso ogni costruzione teorica può realizzarsi praticamente. Migliaia e migliaia di anni fa era abitato da una razza ormai scomparsa che aveva costruito immense città e che aveva raggiunto traguardi ormai del tutto dimenticati.
Oggi, la popolazione dominante è costituita da creature veramente microscopiche che possono solo ammirare i resti dell'antichissima civiltà. La loro tecnologia è praticamente nulla, anche se hanno ottime nozioni di matematica e di fisica. Assomigliano a delle formiche viola (?) e la loro massa è uguale a zero (è o non è una leggenda?). In particolare vi è un luogo famosissimo sul pianeta, chiamato lo scoglio del diamante. Un luogo irraggiungibile dato che è circondato da un oceano profondissimo e si erge come un monolito completamente liscio. La terra ferma è a poca distanza, ma il popolo delle formiche viola non è assolutamente capace di navigare e tanto meno di scalare uno scoglio di tali dimensioni (e senza alcun appiglio). Sulla cima del monolito è stato posto dall'antica civiltà un diamante straordinario, di un valore inestimabile. I tentativi per raggiungerlo sono stati numerosissimi, ma tutti senza alcun risultato.
Un bel giorno si reca sul posto la formica di nome Intellix, dotata di grande intelligenza e fantasia. Davanti a lei si erge lo scoglio con il suo diamante. Attorno a lei i resti di una antica città, di cui restano solo gli strani mattoni con cui era stata costruita. Mattoni conservati perfettamente, tutti uguali fra loro, delle seguenti caratteristiche:
lunghezza = 1 unità
larghezza = 1 unità
altezza (spessore) = 0.1 unità
massa = 1 unità
Dimensioni enormi per la microscopica formica, capace, però, di poterli maneggiare agevolmente, data la sua enorme forza.
La distanza dello scoglio dalla terraferma è di 2 unità, mentre la sua altezza, sempre rispetto alla terraferma è di 3.1 unità.
Intellix riflette a lungo, analizza la situazione, fa un po' di conti e, con l'aiuto dei suoi strumenti di misura accuratissimi (fidatevi!), riesce a raggiungere il diamante e poi a scagliarlo sulla terraferma utilizzando la sua forza esagerata.
Potremmo fare molte domande... ma ne basta una, che comporta la risposta a tutte le altre che possono venire in mente: "Che sistema usa Intellix per raggiungere il diamante?". Data la risposta si potrà, poi, generalizzare il problema con tutte le quantificazioni conseguenti.
Buon divertimento!
N.B.: La formica può camminare in piano e -al massimo- può fare piccoli salti di 0.1 unità.






32 commenti
Ciao e buon anno a tutti.
Nel pianeta Teoria, c'è attrito?
ciao grande Francesco e Buon Anno!
No, si chiama TEORIA proprio perché non esistono tutti quei "disturbi" troppo complicati...
Ok, volevo solo ridurre il numero di mattoni
Come è odioso Teoria: non riesco nemmeno ad immaginarmi come facciano a camminare queste formichine senza un po' di attrito. Ne basterebbe poco poco per arrivare al diamantone con soli 4 mattoni, o con un ponte stile quello di Leonardo.
Comunque dobbiamo costruire una struttura che sia equilibrata ad ogni passo.
Le soluzioni sono tante, cominciamo da quella più "bovina"
Metto un mattone sul bordo del burrone, in modo che per metà lunghezza sia sporgente oltre il bordo stesso: il mattone è in equilibrio.
A questo punto metto due mattoni sopra: il primo lo metto sporgente per metà verso l'interno (la zona di sicurezza). Non ribalta perché anche lui è in equilibrio e quello sotto è appoggiato lungo l'intera metà lunghezza lato sicuro. Il secondo mattone lo metto a sbalzo per metà verso il baratro: è in equilibrio e non fa ribaltare il mattone dello strato sottostante perché equilibrato dal mattone che avevo messo prima.
Ora la luce libera si è ridotta da 2 a 1.
A questo punto devo lavorare di precisione: voglio duplicare i primi due strati sopra quanto già creato.
Appoggio un mattone nella mezzeria del secondo strato, sull'esatta verticale del mattone del primo strato, e sopra questo gli altri due mattoni come nel secondo strato: se continuassi in questa maniera raggiungerei qualsiasi altezza senza però avanzare lateralmente verso il diamantone, e la stabilità sarebbe continuamente garantita. Dovendo però progredire verso destra, devo duplicare i primi due strati per un numero sufficiente di volte in modo da avere peso a sufficienza per uscire ancora senza subire ribaltamenti (non lo calcolo per ora, ma diciamo che con 4-5 duplicazioni dovrei essere a posto).
A questo punto inserisco un mattone a sbalzo sopra il mattone di destra del secondo strato e per equilibrare ne metto uno anche sopra quello di sinistra. La luce si è ridotta da 1 a 0.5 lunghezze.
Basta poco: duplico questo terzo strato (oramai completo) verso l'alto.
Ora inserisco nel quarto strato un nuovo mattone a destra che riduce la luce a zero (si appoggia contro la parete verticale della rupe), e contemporaneamente ne metto uno a sinistra per mantenere l'equilibrio (anche se non è necessario perché il ribaltamento verso il vuoto non è più possibile perché sono appoggiato alla parete).
A questo punto salgo replicando il quarto strato fino a che non raggiungo l'altezza voluta.
E' una soluzione bovina che non mi piace, ce ne sono di più belle mettendo i mattoni anche in verticale ed utilizzando un numero minimo di mattoni.
Ultima osservazione: per salire in quota, la formichina può realizzare una scalinata laterale alla nostra struttura. Ipotizzando che riesca a scalare lo spessore di un mattone, basta fare una scalinata sovrapponendo i mattoni (aggiungendone uno laterale ed uno sopra ad ogni gradino fatto precedentemente)
caro Francesco,
innanzitutto, la formica riesce a scalare il gradino (mi ero dimenticato di dirlo... chiedo scusa). La soluzione dovrebbe essere la più "elegante" e -forse- con il minimo numero di mattoni. In particolare, ricordo che è un problema di FISICA e di MATEMATICA, ossia servono tutte e due per stabilire cosa e come metterla ed essere convinti in anticipo di riuscire. Non è molto che abbiamo parlato di una certa ... "cosa".
Infine, appoggiare alla parete non dà sicurezza (niente attrito). Pensa di arrivare con una differenza di una frazione della formica, in modo da non sfruttare nessun appoggio...
Facciamo così... do un piccolo aiuto: SONO NECESSARI 31 mattoni. Non uno di più....
Grazie per la passione che metti in questi quiz che, in fondo, servono per rendere sempre più pratica e utile la matematica e la fisica!
Certo, ho riportato una soluzione bovina. Appena ho tempo riduco i mattoni e questa volta calcolo. Ciao
E se fosse qualcosa di questo tipo?
http://www.fiaf.net/agoradicult/wp-content/uploads/2013/06/4_101-01-z.jpg
e perché no?! Però attenzione al numero dei mattoni!! Devono essere 31...
Basta fare qualche calcoletto di fisica e poi trovare qualcosa di matematico...
Dici che la formica può scalare un gradino. Ma allora può salire sulla faccia di un mattone in Verticale. Ma allora questo vale anche quando due o più mattoni sono perfettamente uno sopra l altro? Direi di si o sbaglio,? In tal caso basterebbe quel numero minimo di mattoni per coprire la larghezza e mettere sotto 31-n dove n e il numero di tali mattoni. Il problema si ridurrebbe al solo caso orizzontale, che bene o male si risolve subito, anche empiricamente.
No Umberto... può salire lo spessore di 0.1 unità magari saltando, ma non può arrampicarsi su un mattone liscio per 1 unità.
be ma questo non era specificato nel testo.
e poi perchè se può scalare uno 0,1, magari con un mattone in groppa, perchè non può scalare uno 0,2 pari a due mattoni? o uno 0,3? Bisognerebbe chiarire bene cosa può e cosa non può fare la formica
l'ho aggiunto nel testo... di più non posso fare (e ho anche chiesto SCUSA).
Beh... la formica ha un fisico tale da non poter saltare più di 0.1 unità, malgrado sia dotata di forza enorme per il sollevamento pesi e per i lanci. Dato che non è mai stata fatta un'autopsia alla formica aliena bisogna accontentarsi di ciò che riesce a fare e non del perché riesce a farlo. Che vuoi... è o non è aliena? D'altra parte pesa zero e TEORIA è un mondo perfetto.
ok Grazie
ci penserò ancora un po'.
Strani mattoni tutti uguali fra loro, delle seguenti caratteristiche:
lunghezza = 1 unità
larghezza = 1 unità
altezza (spessore) = 0.1 unità
massa = 1 unità
Microscopica formica con enorme forza.
Distanza scoglio terraferma 2 unità.
Altezza 3.1 unità.
Salti di 0.1 unità.
Quindi la formica sistema 30 mattoni in orizzontale. Ruota la pila di 45°, con uno spigolo appena fuori dalla terraferma.
Spinge i 29 mattoni soprastanti il primo, ecc. .
Al gradino 25 o 26 sistema un mattone in verticale sullo spigolo verso la terraferma.
Spinge dal mattone 30 , 29 ,28 , 27, fino quasi farli cadere.
(*)
caro Gianfranco,
tu dici:
Spinge i 29 mattoni soprastanti il primo, ecc. .
Al gradino 25 o 26 sistema un mattone in verticale sullo spigolo verso la terraferma.
Spinge dal mattone 30 , 29 ,28 , 27, fino quasi farli cadere.
Dovresti spiegare come e di quanto spinge i 29 mattoni. Il mattone in verticale a cosa serve? E poi, nuovamente dici spinge 4 mattoni fino quasi a farli cadere...
Ti giuro che non riesco a capire il tuo procedimento (ci vorrebbe una figura) e poi vogliamo un risultato calcolabile e quantitativo e non una soluzione che usa "spinge" e "fino quasi a...".
Se vuoi mandare una figura, me la puoi inviare tramite i contatti e io la pubblico...
Ora non posso usare l’”i7”. In TEORIA il baricentro del mattone 30 si trova sulla diagonale, e deve essere appena all’interno dello spigolo del mattone 29, che deve sporgere di meno per il peso sopra a sbalzo. Il 28 ancora meno.
Con il mattone in verticale nel gradino 26, il baricentro si sposta nuovamente verso sinistra. Altrimenti i mattoni sopra si ribaltano.
Propongo un procedimento che mi sembra corretto, ma non risolve il problema e non so se l'errore è nel calcolo oppure nel ragionamento:
Per raggiungere il diamante voglio costruire una semplice scala impilando i mattoni uno sull'altro e facendoli sporgere in modo uniforme come se fossero dei normali gradini.
Per salire 3,1 in verticale mi servono 3.1/0.1=31 mattoni
Per percorrere 2 in orizzontale devo far sporgere ogni mattone di almeno 2/31=0,06451etc ed essere anche sicuro di garantire l'equilibrio statico della scala.......
Per comodità faccio le seguenti assunzioni:
considero i mattoni di lunghezza parametrica 2L
considero momentaneamente tutti i mattoni impilati uno sull'altro e messi esattamente sul bordo della terraferma e numerati partendo dal basso verso l'alto in modo tale che il mattone 1 sia quello più basso e il mattone 31 sia quello più in alto
considero un sistema xOy centrato sul vertice della terraferma
In questa configurazione l'ascissa del centro di massa Cx della pila di mattoni è -L e l'equilibrio statico è assicurato.
Da questa situazione iniziale provo a creare una scala spostando verso destra il mattone 1 di una quantità x, il mattone 2 di una quantità 2x ...... il mattone 31 di una quantità 31x in modo tale che ogni mattone sia x più a destra rispetto al mattone di sotto. Così facendo ottengo una scala i cui gradini sono costituiti dai singoli mattoni.
In questa nuova configurazione l'ascissa del centro di massa Cx sarà:
31*Cx= (-L+x) + (-L+2x) + (-L+3x) + ......... + (-L+31x) = -31*L+x*(1+2+3+.....+31)=-31*L+x*16*31
Per garantire l'equilibrio statico della scala impongo che Cx sia sul vertice della terraferma ossia Cx=0 quindi
L=x*16 cioè il massimo spostamento consentito verso destra è x=L/16
Se il mattone è lungo 1 allora 2L=1 quindi L=1/2 quindi x=1/32 e con 31 mattoni arrivo a 31/32<2
Se metto il mattone in diagonale allora 2L=sqrt(2) quindi L=sqrt(2)/2 quindi x=sqrt(2)/32 e con 31 mattoni arrivo a sqrt(2)/32*31<2
Quindi in entrambi i casi non riesco a raggiungere lo scoglio.
Come dicevo all'inizio non so se l'errore è nel calcolo oppure nel ragionamento.........
direi più nel ragionamento, forse un po' troppo empirico...
Possiamo evitare di mettere i mattoni in diagonale per semplificare i calcoli...
ho fatto anche io dei conti analoghi a quelli di MarcoC ma la stabilità della scala non mi torna. Probabilmente anche io sto sbagliando qualcosa.
Ricordiamoci che siamo su TEORIA ...
Provate a fare una figura...
se la gradinata deve essere una gradinata, c'è poco da fare.Poi , Deve quadrare sia in orizzontale che in verticale. e devono in ogni caso essere 31, visto che lo hai detto anche tu.Immagino che tu stia usando dei concetti un po' più avanzati, da quello che intuisco dal testo. Non resta che aspettare.
Per costruire la gradinata bisogna fare un po' di calcoli di tipo "fisico", poi si vedrà che basta avere mattoni e si può fare quello che si vuole su TEORIA. 31 mattoni sono il minimo per alzarsi di 3.1 unità... tutto lì.
mi rimangio tutto. Ho rifatto i calcoli e torna tutto . Ho bisogno però per scriverlo di essere davanti al computer. Son qua col cellullare.
Ottimo!
Parafrasando Archimede, in questo caso direi: datemi in numero sufficiente di leve e salirò il mondo.
Infatti è l'equilibrio della leva che mi dice quanto può sporgere ciascun scalino.
Considero lo scalino n-esimo come il braccio di una leva. Avrà sopra di se 31-n gradini che considero posizionati come baricentro all'estremo destro del braccio. Mi domando: dove deve essere il fulcro della leva affinchè il tutto sia in equilibrio?
Chiamo x il braccio destro della leva, cioè la sporgenza del gradino n-esimo rispetto al precedente.
A sinistra del fulcro c'è il solo peso proprio della parte di gradino (1-x) con baricentro distante dal fulcro (1-x)/2.
A destra del fulcro c'e il peso prorio della parte di gradino x con baricentro distante dal fulcro x/2 e ci sono tutti i restanti gradini (31-n) con baricentro distante dal fulcro x.
L'equilibrio si ha quando^2}{2}=\frac{x^2}{2}+(31-n)x) .
.
Quindi il gradino può sporgere rispetto al precedente di}) con n da 1 a 31.
con n da 1 a 31.
Il primo solo di 0,016, il 10° di 0,0227 , il 20° di 0,041 e l'ultimo di 0,5.
La somma di tutte le sporgenze, che dà la distanza dal bordo, è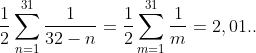
C'è un piccolo margine per non mettersi al limite su tutti i gradini.
Certamente non è una struttura antisismica, ma in TEORIA può reggere.
Direi che il succo è questo... anche se io ho calcolato il baricentro di mattone in mattone... e la serie viene fuori immediatamente.
Preparo la risposta e intanto vediamo se Umberto mi manda la sua figura...
scusa ma da ieri sono in H a far flebi di patassio...
comunque, visto che ti preme tanto saperlo, ho fatto come te , calcolando baricentro mattone per mattone. Ma il metodo di Fabrizio mi sembra più bello. É qualcosa di simile alla ricorsione. Complimenti a Fabrizio .
Intanto auguro ad Umberto un rapido ritorno a casa.
Aggiungo due figure che vorrebbero illustrare quanto detto sopra.
La prima visualizza il posizionamento dei gradini.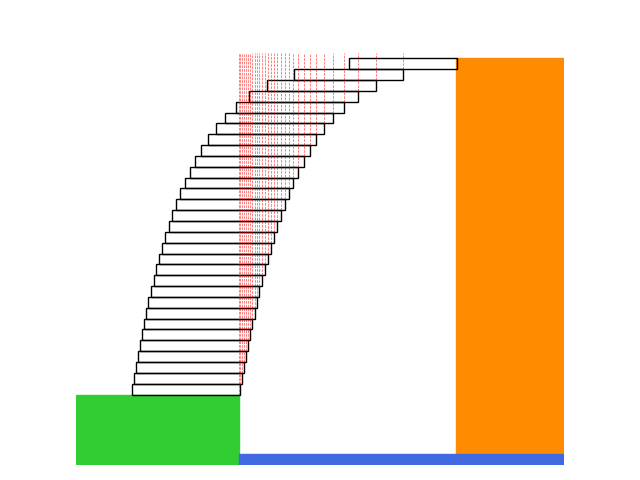
Le linee rosse sono le verticali dei baricentri di ciascuna parte della struttura.
Con questo posizionamento il baricentro dell'intera gradinata (linea rossa più a sinistra) si trova sulla verticale del bordo della terraferma. Ma questo non basterebbe per la stabilità teorica della struttura. Occorre anche che la struttura sopra ciascun gradino abbia il baricentro entro il bordo del gradino sottostante.
La figura sottostante visualizza gli elementi per trovare questo posizionamento.
Nell'esempio siamo al 29° gradino. Ci sono altri due gradini sovrastanti. Impongo che il loro baricentro sia al limite del 29° gradino. Devo trovare di quanto si può far sporgere il gradino (parte rossa) con ancora il peso della parte verde che riesce a controbilanciare il peso della parte rossa ed dei gradini sovrastanti. Le forze (F) ed i momenti (m) in gioco sono riportati nella parte alta della figura. Questa configurazione porta alla equazione dell'equilibrio ed alla soluzione che ho inserito nel mio comento precedente.
I gradini 30 e 31 sono tratteggiati perchè andranno riposizionati, pur mantenedo il loro baricentro nella stessa posizione. Per rendere meglio visibili gli elementi in figura, la sporgenza del gradino è maggiore del consentito teorico.
tanti auguri anche da parte mia Umberto
grazie. Non ne avrò per molto.