Questo articolo va ben oltre il teorema di Tolomeo (di cui abbiamo iniziato a parlare QUI) e introduce una interessantissima trasformazione che si applica al piano euclideo. La sua importanza è enorme in quanto riesce a semplificare molti problemi geometrici, tra cui dare una dimostrazione quasi "ridicola" del teorema di Tolomeo. L'affronteremo solo superficialmente, ma quanto dovrebbe bastare a comprenderne i risvolti più nascosti e generali. Alla fine scriverò una delle mie solite esternazioni e mi aspetto commenti e critiche più che giustificate... Insomma, non perdetevi questo articolo e non consideratelo solo una piccola tessera legata al grande genio di Tolomeo.

Trasformiamo un piano in un cerchio e viceversa

Un minimo di storia... L'inversione geometrica o geometria inversiva si deve al matematico tedesco Ludwig Immanuel Magnus (1790 - 1861). Tra il 1812 e il 1815 partecipò alle guerre napoleoniche e ... permettetemi di ipotizzare che abbia risentito della strepitosa capacità matematica e geometrica di Napoleone, espressa nelle sue battaglie... Tra il serio e il faceto, introduciamo  una prima "rozza" spiegazione dell'inversione geometrica.

Essa, in qualche modo, è una trasformazione nel piano euclideo. Ma una trasformazione ben diversa da quelle che siamo abituati a conoscere, quali la traslazione, la rotazione, il ribaltamento speculare e l'ingrandimento o il rimpicciolimento (lo "zoom"). Queste sono trasformazioni che lasciano inalterata la forma di una figura geometrica, mentre l'inversione la deforma completamente.

Le sue applicazioni sono molteplici, non ultime la trasformazioni di moti circolari in moti lineari. Ricordiamo tra l'altro che una parabola e un'iperbole si trasformano in una cardioide e in una lemniscata di Bernoulli (e viceversa). L'inversione ha anche permesso di risolvere problematiche legate all'antica grecia e mai chiarite completamente. In questo articolo, tuttavia, rimarremo legati a quanto interessa per avere una elegantissima e "raffinata" dimostrazione del teorema di Tolomeo o poco più (l'avevamo già dimostrato QUI, ma adesso è tutta un'altra cosa...). Troverete, comunque, modo di divertirvi a costruire figure più o meno strane, dato che il meccanismo utile per ottenere l'inversione è di estrema semplicità.

In parole povere, uno dei primi scopi è quello di trasportare TUTTI gli infiniti punti del piano euclideo all'interno di un cerchio di raggio qualsiasi, che possiamo chiamare cerchio di inversione. I punti, come ben sappiamo dalla matematica, che ci  spiega con passione e competenza Umberto, rimangono infiniti. Così come si può trasportare all'interno del cerchio, così l'operazione inversa trasporta i punti interni al cerchio nei punti del piano "esterno". Vi è anche la possibilità di estendere il tutto allo spazio, ma noi ci limiteremo al piano, dato che miriamo al teorema di Tolomeo.

Cominciamo con il dire qualche banalità che, però, diventa essenziale per il tipo di approccio. Una inversione seguita dal suo contrario lascia l'insieme totale INVARIATO e questo è come dire che l'inversione moltiplicata per l'operazione opposta porta all'unità, ossia alle condizioni iniziali.

Visto che abbiamo parlato di Napoleone e della sua celebre strategia bellica, immaginiamo di potere utilizzare l'inversione in un campo di battaglia, ad esempio durante un assedio. Ce lo mostra la Fig. 4 dove al posto del cerchio abbiamo inserito un bel castello a pianta circolare.

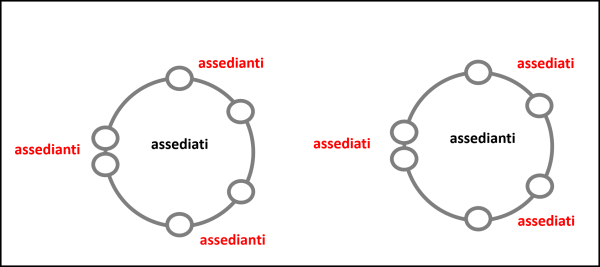
Bene, se potesse essere usata dagli assediati, essi potrebbero trasformarsi in assedianti e gli assedianti in assediati. Immaginatevi la sorpresa di chi si trovava libero di agire e di vietare l'ingresso nella città ridotta alla fame e che improvvisamente si ritrova nelle condizioni del nemico ormai allo stremo. Chissà che Napoleone non abbia proprio pensato a una magia del genere e non l'abbia trasportata nella mente di quel "nemico" così intelligente?

Bando agli scherzi, passiamo alla descrizione della manovra che bisogna fare per trasportare un punto del piano esterno in un punto interno al cerchio. Ce lo illustra in modo quasi banale la Fig. 5.

Sia P il punto esterno che vogliamo trasferire all'interno del cerchio. Tracciamo da P la tangente al cerchio (ne basta una, perché anche usando l'altra si otterrebbe lo stesso punto finale) e la congiungente P con il suo centro O. Dal punto di tangenza T tracciamo la perpendicolare alla retta OP fino a incontrarla in P1. Bene, P1 è il punto P che ha subito l'inversione. Ovviamente, lo stesso procedimento, eseguito al contrario, riporta il punto P1 in P, come mostra la Fig. 6.

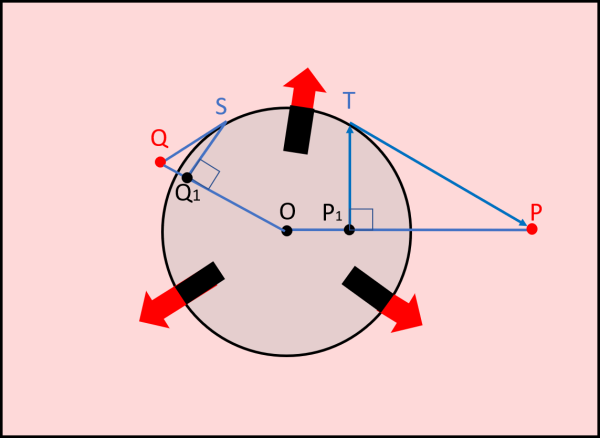
Basta tracciare la retta OP1 e poi la perpendicolare a questa retta da P1 fino a incontrare la circonferenza in T. Da T tracciare la tangente fino a incontrare la retta OP1 in P. Come già detto, tutto torna come all'inizio.

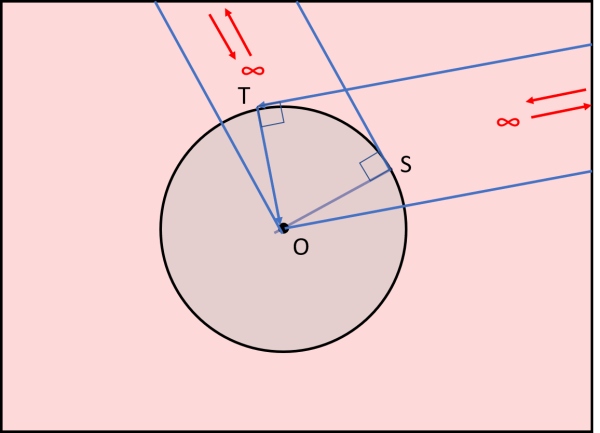
Normalmente si cerca di trascurare il centro O del cerchio d'inversione, ma esso acquista il suo logico significato se consideriamo il piano ampliato, con tanto dei suoi punti all'infinito. Una punto all'infinito del piano viene rappresentato da una qualsiasi insieme di rette parallele che si incontrano proprio nel punto all'infinito. Tra queste consideriamo proprio quella tangente alla circonferenza e quella che passa per il centro O. Se dal punto di tangenza tracciamo la perpendicolare alla retta che passa per il centro intersechiamo quest'ultima proprio nel centro O (Fig. 7). Ovviamente, vale anche il viceversa. Il centro O può essere trasformato in qualsiasi punto all'infinito del piano.

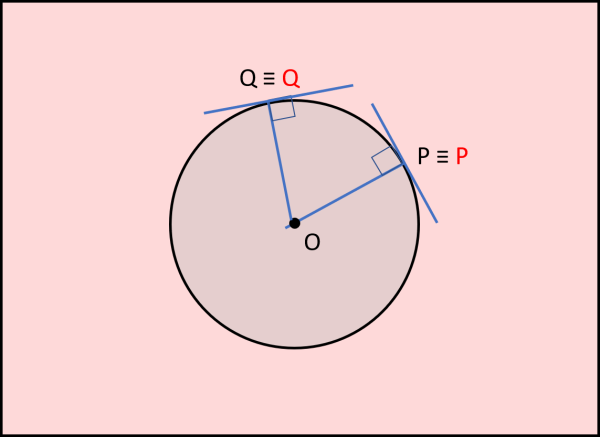
Vi sono altri punti particolari da studiare? Sicuramente sì: quelli che appartengono alla circonferenza. Tracciamo in Fig. 8 la congiungente P con il centro O. Nello stesso tempo tracciamo la tangente alla circonferenza da P. Il punto in cui questa tangente tocca la circonferenza è proprio P. Ovviamente tracciare da lui la perpendicolare alla retta PO vuol dire rimanere fermi nel punto P. In parole ultra semplici: i punti della circonferenza si trasformano in loro stessi. Un bel risultato, estremamente democratico!

Finora abbiamo trattato solo con punti. Passiamo ora a vedere come si trasforma una retta. Pensate, forse, che, dato che essa è composta dagli stessi punti trasformati, diventi ancora una retta? Nemmeno per sogno o, almeno, lo fa solo in un caso molto particolare che andiamo subito a trattare:

Consideriamo, in Fig. 9, una retta che passa per il centro O.

Consideriamo anche un paio di punti (rossi) esterni al cerchio e applichiamogli l'inversione. Essi finiscono ancora sulla retta di partenza, anche se nella sua parte interna al cerchio. Analogamente, se prendiamo due punti (neri) della retta, interni al cerchio, essi si trasferiscono in due punti esterni. In altre parole, la retta si trasforma in se stessa!

Consideriamo adesso, in Fig. 10, una retta del tutto esterna al cerchio di inversione e prendiamo un certo numero di punti per riuscire a capire bene cosa viene fuori.

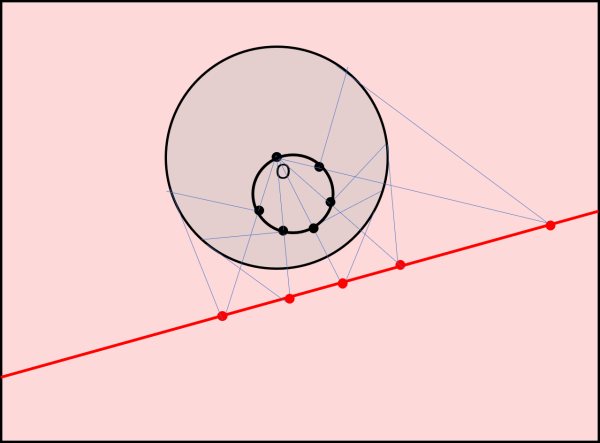
Non è difficile arrivare alla conclusione, senza bisogno di applicare formule: una circonferenza interna al cerchio che passa sempre per il centro d'inversione O. La spiegazione è perfettamente logica, dato che il punto O corrisponde, come abbiamo già visto, al punto infinito della retta. Finalmente abbiamo avuto una vera trasformazione, avendo ottenuto una circonferenza a partire da una retta (e viceversa, ovviamente).

Abbiamo in mano quanto basta per tornare al nostro Teorema di Tolomeo. Tuttavia, concediamoci prima qualche divagazione che potrebbe benissimo essere saltata, volendo andare al sodo...

In giro per il piano

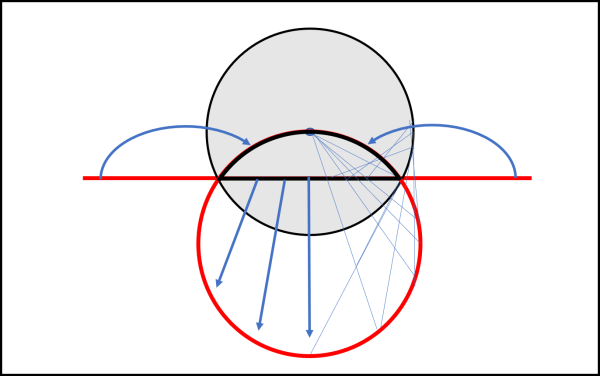
A questo punto, siamo in grado di andare avanti da soli e provare con tutte le figure più o meno conosciute. Tracciamo, ad esempio, una retta che intersechi il cerchio d'inversione, senza passare per il centro. Bene, la parte esterna rossa si trasforma nell'arco di cerchio nero che DEVE passare per il centro, mentre la parte interna nera si trasforma nel cerchio rosso esterno. Ne segue che l'intera retta si è trasformata nuovamente in una circonferenza che passa per il centro di inversione O, ma è parte interna e parte esterna al cerchio d'inversione (Fig. 11).

Pensiamo, adesso, a un triangolo esterno al cerchio. Bene, esso si trasforma in tre archi di circonferenza che formano un triangolo curvilineo che mantiene per costruzione gli stessi vertici (trasformati) del triangolo iniziale. Si potrebbe anche dimostrare che si mantengono gli angoli, dove per angoli del triangolo curvilineo si intendono gli angoli tra la tangenti delle circonferenze che confluiscono nei vertici (Fig. 12)

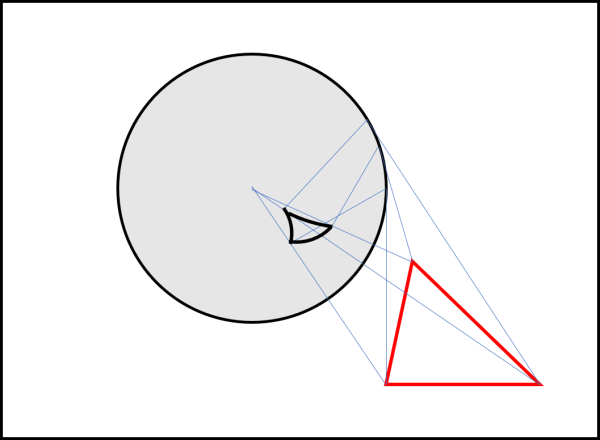
Ovviamente i tre archi di circonferenza fanno parte di circonferenze che devono passare per O, dato che i lati iniziali del triangolo fanno parte di rette che non passano per il centro di inversione. In modo analogo, un triangolo a lati rettilinei interno al cerchio si trasforma in un triangolo curvilineo esterno.

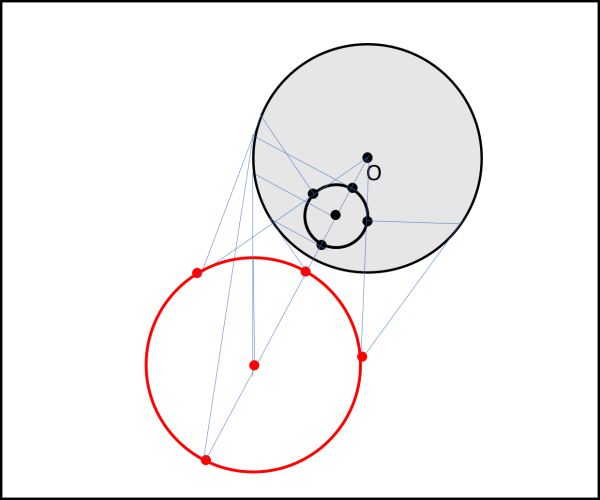
Cosa succede invece a una circonferenza completamente esterna al cerchio?  Basta eseguire la costruzione per punti e si nota quasi subito che si ottiene una nuova circonferenza (di raggio diverso) completamente interna al cerchio. In questo caso, però, la circonferenza interna NON passa per il centro O.  Come al solito, vale anche il viceversa (Fig, 13). Attenzione: il centro di inversione va all’infinito, è solo il centro del cerchio interno che va nel centro del cerchio esterno.

Vediamo, infine, in Fig. 14, cosa capita a un cerchio che interseca il cerchio di inversione ma NON passa per il suo centro. Bene, non possiamo fare altro che ottenere un cerchio nero di raggio diverso che NON passa per il centro. I due cerchi devono però intersecarsi nei punti appartenenti alla circonferenza del cerchio d'inversione.

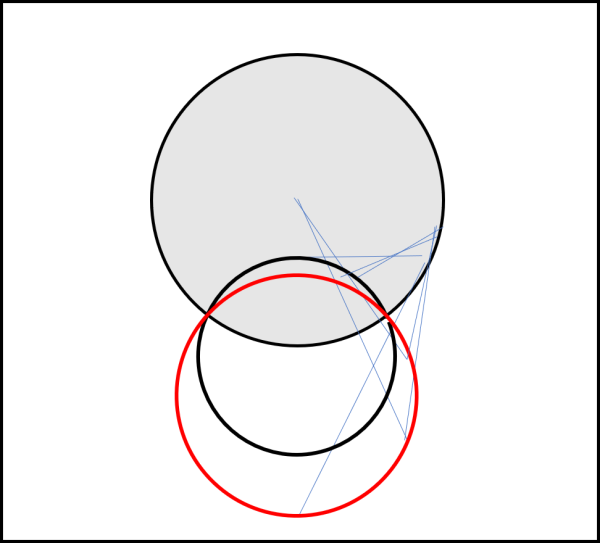
Provate pure a trasformare una parabola esterna o intersecante il cerchio e ne vedrete delle belle, come già menzionato precedentemente. Dobbiamo, comunque, fermarci qui, dato che il nostro scopo era solo quello di dimostrare il teorema di Tolomeo con la formula più semplice possibile. Non solo eleganza ma massima semplicità.

Dimostriamo il Teorema di Tolomeo

Possiamo, perciò, tornare alla fase fondamentale della costruzione e ragionare in termini di retta completamente esterna al cerchio d'inversione. Tutto il resto è stato un di più. Un di più veramente stringato dato che le applicazioni della geometria inversiva o inversione geometrica (come preferite) sono praticamente infinite oltre che essere descrivibili in termini analitici, nemmeno troppo complicati, vista la banalità dell'azione necessaria all'inversione.

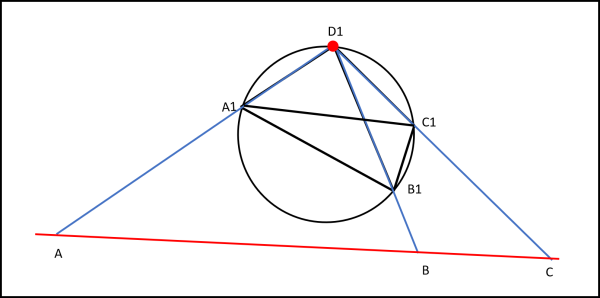
Prendiamo un bel cerchio e iscriviamogli dentro un quadrilatero qualsiasi. Cosa possiamo dire ragionando su un piano in cui viene applicata la geometria inversiva? Beh... questo cerchio potrebbe benissimo essere il cerchio che corrisponde a una retta esterna al cerchio di inversione. Attenzione: il cerchio che abbiamo considerato NON è il cerchio di inversione ma un cerchio a lui interno. Cosa possiamo dire senza fare tanti calcoli? Se questo cerchio deve essere quello che si trasforma in una retta esterna DEVE passare per il centro del cerchio d'inversione. Qualcosa come quella che vediamo nella Fig. 15.

Ad esempio potremmo prendere un punto O qualsiasi e tutto andrebbe bene. Ovviamente la retta che abbiamo tracciato non ha niente a che vedere con il cerchio collegato al quadrilatero ma l'abbiamo disegnata tanto per rendere l'idea. Qual è la cosa veramente importante da sapere e ricordare? Che i punti della retta, che corrispondono ai 4 vertici del quadrilatero, devono stare sulle rette che partono dal centro O scelto a caso e i quattro vertici del quadrilatero. Questo deve essere vero per la costruzione stessa dell'azione di inversione.

Siano, ad esempio A, B , C e D i punti corrispondenti ai vertici A1, B1, C1 e D1. Ripeto ancora: non tenete conto delle distanze tra A1 e A (e simili) e delle distanze tra A e B (e simili), Tuttavia, abbiamo un piccolo problema... I punti che entrano in gioco sono quattro, mentre il nostro scopo è ricavare il teorema di Tolomeo nel modo più banale possibile, con l'operazione geometrica forse più facile fra tutte. Vi ricordate? Ne avevamo già accennato all'inizio degli articoli su Tolomeo...

Vogliamo dimostrare il teorema attraverso l'operazione illustrata nella Fig. 16, ossia attraverso una ridicola somma di segmenti, che può essere eseguita anche da un bambino delle elementari: Il segmento AB più il segmento BC è uguale al segmento AC.

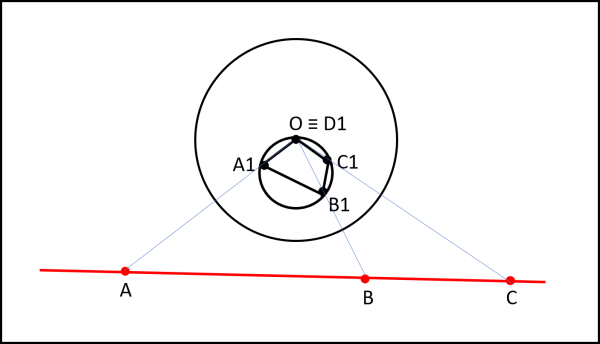
Il problema dei 4 punti si risolve immediatamente: basta considerare come centro del cerchio di inversione il punto D1 (ad esempio). La Fig. 15 diventa la Fig. 17.

Per non confonderci, riportiamo in Fig. 18 la situazione nella sua globalità, con tanto di cerchio d'inversione.

A questo punto possiamo riprendere la Fig. 6, che illustrava il passaggio da un cerchio interno al cerchio d'inversione (passante per il centro d'inversione) e la retta esterna corrispondente. La riproponiamo in Fig. 19, dove abbiamo solo l'accortezza di disegnare anche il segmento OT = r.

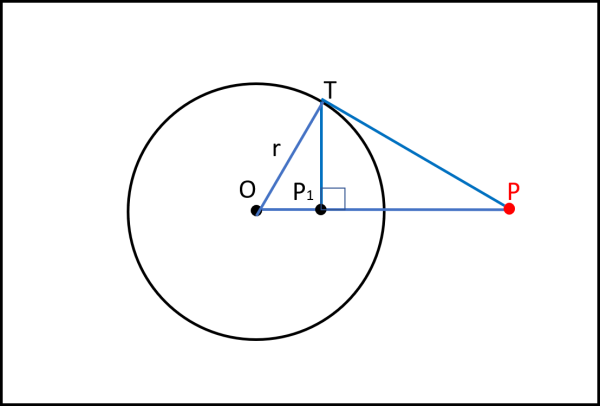
Nella figura si notano ben tre triangoli rettangoli simili per costruzione. A noi interessano OP1T e OPT. Notiamo che OT è proprio il raggio r del cerchio d'inversione. Possiamo scrivere:

OP1/r = r/OP

da cui

OP · OP1 = r²                      .... (1)

Abbiamo una prima relazione tra le distanze del centro d'inversione dai due punti (l'uno il trasformato dell'altro). Notiamo che questa relazione vale per qualsiasi punto trasformato (in un verso o nell'altro) dato che r² è una costante!

Riprendiamo ora la Fig. 18 e ne facciamo uno "zoom" in Fig. 20, in modo da vedere bene un'altra coppia di triangoli. Per mettere in luce la generalità della configurazione, chiamiamo  P1 e Q1 due punti che hanno subito l'inversione in P e Q (e viceversa).

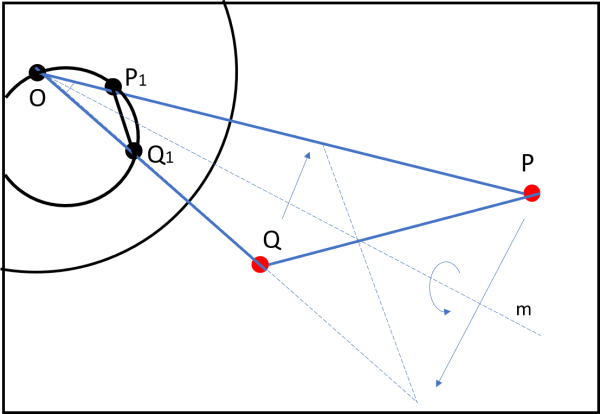
Siamo di fronte a due triangoli: OP1Q1 e OPQ. Sembrano completamente diversi, ma non facciamoci ingannare. Per non rischiare conclusioni affrettate consideriamo nuovamente la (1). Essa è una formula generale e allora deve poter valere per qualsiasi coppia di punti trasformati uno nell'altro. In  particolare possiamo scrivere:

OP · OP1 = r² = OQ · OQ1

O ancora:

OP1/OQ = OQ1/OP              .

Vi è proporzionalità tra i lati dei due triangoli e, inoltre, essi hanno l'angolo in O in comune. Ne segue che i due triangoli sono simili (per vederlo meglio basta ruotare il triangolo OPQ attorno alla retta m e salta subito all'occhio  la loro similitudine...).

Possiamo perciò scrivere anche:

Q1P1/QP = OP1/OQ

QP = Q1P1 · OQ/OP1   ... (2)

Ma ricordando la (1)

QP = Q1P1 · r²/(OP1 · OQ1)        .... (3)

La (3) è importantissima perché mette in relazione la distanza tra due punti della retta con segmenti che appartengono all'inversione.

Possiamo finalmente passare al nostro quadrilatero qualsiasi A1B1C1D1, ricordando che nel nostro caso O = D1.

Vale la pena ripetere che questo quadrilatero, essendo inscritto in un cerchio che passa per il centro del cerchio d'inversione D1, si deve trasformare in una retta esterna che passa per A, B e C. Ma adesso abbiamo tutti i dati per scrivere le relazioni tra i punti e le loro distanze reciproche! Consideriamo nuovamente la Fig. 18 che, come già detto, non rappresenta la vera situazione, ma basta per capire la trasformazione. D'altra parte, ormai abbiamo le vere distanze con cui giocare.

Applicando la (3) ai tre segmenti AB, BC e AC abbiamo:

AB= A1B1 · r²/(D1A1 · D1B1)

BC = B1C1 · r²/(D1B1 · D1C1)

AC = A1C1 · r²/(D1A1 · D1C1)

Ora non ci resta che mantenere le promesse. Avevamo detto che il Teorema di Tolomeo si dimostrava sommando tra loro due segmenti? E questo facciamo, ossia scriviamo la banalissima operazione:

AB + BC = AC

A1B1 · r²/(D1A1 · D1B1) + B1C1 · r²/(D1B1 · D1C1) = A1C1 · r²/(D1A1 · D1C1)

Semplifichiamo, eliminando r² (punto fondamentale che ci dice che l'inversione è indipendente dal raggio del cerchio d'inversione), e poi riduciamo al minimo comune denominatore che è (D1A1 · D1B1 · D1C1). La relazione precedente diventa:

A1B1 · D1C1/(D1A1 · D1B1 · D1C1) + B1C1 · D1A1/(D1A1 · D1B1 · D1C1) = A1C1 · D1B1/(D1A1 · D1B1 · D1C1)

Semplifichiamo il denominatore e abbiamo:

A1B1 D1C1 + B1C1 D1A1 = A1C1 D1B1

Che non è altro che il Teorema di Tolomeo applicato al quadrilatero A1B1C1D1 !

Conclusioni (molto personali)

Che dire? Sembra proprio di avere usato una bacchetta magica. Probabilmente si potrebbero fare altre riflessioni e io non me le faccio mancare (sapete come sono fatto). Attraverso azioni tipiche della geometria euclidea siamo riusciti a mettere in relazione punti del piano inseriti in un "doppio stato": quelli esterni a un cerchio e quelli interni al cerchio. In altre parole, ogni punto del piano si può presentare sotto una duplice veste. Abbiamo visto che scegliendo la veste che più ci è comoda alcune relazioni si semplificano in modo straordinario. Non sentite -forse- un leggere profumo di Meccanica Quantistica? Ma la faccenda va ancora oltre... Curve particolarmente strane, se trattate con le regole classiche, si trasformano in curve estremamente banali cambiando stato ai punti. Siamo sicuri di affrontare le problematiche della Natura sempre con il sistema più semplice? Forse non sempre... Basta un po' di geometria alla portata delle scuole medie per riuscire a semplificare e a trasformare azioni, apparentemente complesse, in processi sempre più banali e immediati. Pensiamo in grande... ai moti circolari e curvilinei, alle reazioni fisiche e a tutta la Natura... Abbiamo realmente scelto la via o le vie migliori per interpretarla? Che ne direste se un giorno una certa trasformazione di livello elementare ci premettesse di scrivere come semplici somme o sottrazioni tutta la teoria della Relatività? Sto sicuramente volando con la fantasia, ma nel meraviglioso Teatro dell'Universo il copione può sempre essere interpretato in tanti modi. Altro che multiversi, basta solo saper vedere, accettare ed essere pronti a seguire con entusiasmo certe stranezze che tali sono per noi ma non per la Natura. La Meccanica Quantistica insegna. In fondo, tutta la Natura è un infinito Paese delle Meraviglie e i bambini ne posseggono la chiave. Non facciamogliela perdere!

 

QUI tutti gli articoli dedicati al Teorema di Tolomeo