Mettiamoci alla prova con la Relatività Generale - Vettori e trasformazioni di coordinate, sviluppi per la seconda domanda

  • Home
  • Articoli
  • Fisica
  • Relatività
  • Mettiamoci alla prova con la Relatività Generale - Vettori e trasformazioni di coordinate, sviluppi per la seconda domanda
24/12/20

Mettiamoci alla prova con la Relatività Generale - Vettori e trasformazioni di coordinate, sviluppi per la seconda domanda

Categorie: Relatività Tags: Scritto da: Fabrizio Commenti:2

Questo articolo fa parte della sezione "METTIAMOCI ALLA PROVA!" all'interno della Relatività Generale al microscopio

 

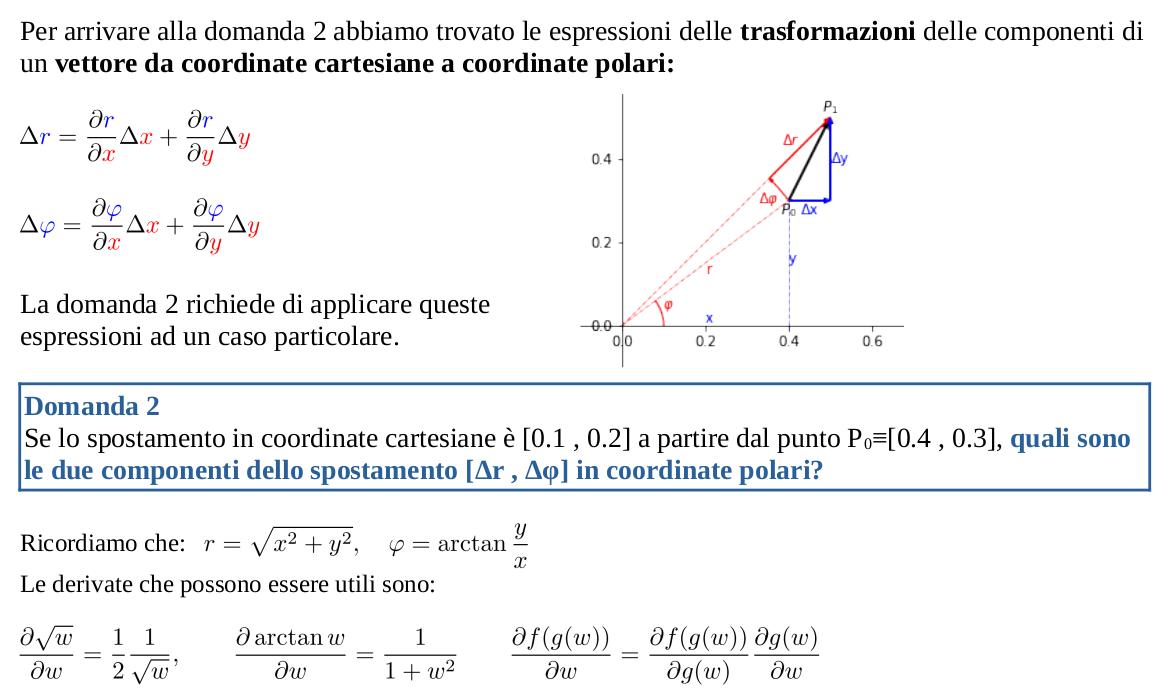
La domanda 2 del precedente articolo è un poco più difficile delle altre poiché richiede il calcolo di alcune derivate non banali.

Descrivo qui i passaggi in modo che chi li ha portati a termine possa confrontare la soluzione trovata e chi non è riuscito ad arrivare in fondo possa avere un aiuto.

Devo anche dire che questi sviluppi non sono necessari per proseguire la lettura dell'articolo e rispondere alle successive domande.

Trasformazioni componenti vettori da coordinate cartesiane a coordinate polari

 

Trasformazione componenti vettori da coordinate cartesiane a coordinate polari per ottenere la componente radiale

\large \Delta { {\color{Blue} r}}=\frac{\partial {\color{Blue} r}}{\partial {\color{Red} x}} \Delta {\color{Red} x}+\frac{\partial {\color{Blue} r}}{\partial {\color{Red} y}} \Delta {\color{Red} y}= \frac{x}{\sqrt{x^2+y^2}}\Delta {\color{Red} x}+\frac{y}{\sqrt{x^2+y^2}}\Delta {\color{Red} y}

 

 

Passiamo alla seconda componente in coordinate polari, Δφ. Lo sviluppo è molto simile al precedente.

Per chi non lo ha portato a termine, potrebbe essere interessante procedere da solo con questo sviluppo partendo dalla espressione generale:

\large \Delta {\color{Blue} {\color{Blue} \varphi}}=\frac{\partial {\color{Blue} \varphi}}{\partial {\color{Red} x}} \Delta {\color{Red} x}+\frac{\partial {\color{Blue} \varphi}}{\partial {\color{Red} y}} \Delta {\color{Red} y}

Si tratta ancora sostituire nel termine a destra la variabile in coordinate polari con la sua espressione in coordinate cartesiane. Quindi di derivare una funzione di funzione. In questo caso la funzione f è arctan che ha come argomento la funzione \large \frac{y}{x}. Quest'ultima la devo considerare una volta funzione di x e considerare y costante ed una volta funzione di y e considerare x costante.

Ricordo le espressioni che potrebbero essere utili:

\dpi{100} \large \varphi=\arctan{\frac{y}{x}},\qquad \frac{\partial \arctan{w}}{\partial w}=\frac{1}{1+w^2}

\dpi{100} \large \frac{\partial f(g(w))}{\partial w}=\frac{\partial f(g(w))}{\partial g(w)}\frac{\partial g(w)}{\partial w},\qquad \frac{dw^n}{dw}=nw^{n-1}

 

Questo è lo sviluppo della espressione.

Trasformazione componenti vettori da coordinate cartesiane a coordinate polari per ottenere la componente azimutale

Trasformazione componenti vettori da coordinate cartesiane a coordinate polari

Trasformazione componenti vettori da coordinate cartesiane a coordinate polari e calcoli numerici

Articoli correlati

2 commenti

  1. Giangiacomo
    30/06/2023 at 17:53

    Questo articolo sulla trasformazione delle componenti di un vettore controvariante da un sistema di coordinate a un altro lo trovo davvero illuminante!

    Però la formula di partenza  Vym= Σi  ∂ym / ∂xi Vxi non la ho trovata nelle prime 7 sezioni di teoria, di questi articoli sulla Relatività Generale, anche se sembra davvero basilare! Mi è sfuggito qualcosa?

    La formula suddetta sembra apparentata alla formula (1) di trasformazione del gradiente dell'articolo 4 sui campi. Forse perché il gradiente produce dei vettori?

    Sarebbe anche molto interessante conoscere la formula di trasformazione dei vettori covarianti da un sistema di coordinate ad un altro.

    Ringraziamenti!!!

  2. Fabrizio
    09/01/2024 at 12:14

    Giangiacomo, mi scuso per la mancata risposta alla tua domanda.

    Provo a rispondere ora, sperando che possa comunque leggere la risposta.

    La trasformazione dei vettori è stata introdotta nella espressione (3) in questo articolo.

    La relazione tra le trasformazioni dei vettori e le trasformazioni dei gradienti è molto stretta perché il prodotto tra gradiente e vettore deve dare uno scalare che non dipende dalle base di coordinate impiegata. Quindi le due trasformazioni devono conservare il valore dello scalare.

    Le trasformazioni dei vettori covarianti sono quelle dei gradienti. In molti testi più recenti si preferisce riservare la denominazione di vettore ai vettori controvarianti e chiamare in altro modo i vettori covarianti. Il gradiente è un caso particolare di questa denominazione.

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.