Questo è il settimo articolo della serie "La Relatività Generale al microscopio"

 

Finalmente possiamo entrare nel mondo del tensore di rango due. Innanzitutto, abbiamo bisogno di DUE vettori, ciascuno con tutte le sue belle coordinate in un certo sistema di riferimento. La singola coordinata viene individuata dal suo apice (x¹, x², x³,...). Il numero di coordinate indica, ovviamente, le dimensioni in cui stiamo lavorando. In poche parole, prendiamo un vettore A^m e un altro vettore Bⁿ, ricordando ancora una volta che sia m che n possono assumere tutti i valori che contraddistinguono le loro coordinate.

Scriviamo una qualsiasi combinazione tra di loro:

A^m Bⁿ

Questa combinazione la chiamiamo tensore T^mn, ossia:

T^nm = A^m Bⁿ

Questo è un tensore di rango 2 e non differisce da quello che abbiamo usato per descrivere il lavoro... solo che in quel caso il valor massimo di m e n era uguale a 2 (spazio a due dimensioni).

A costo di essere noioso, controlliamo nuovamente se abbiamo compreso bene la formuletta appena scritta. Se m e n possono arrivare solo a 2 (due dimensioni) esistono 4 combinazioni tra le coordinate di A e B e il tensore T ha 4 componenti. Se n = 3, esistono 9 componenti di T  e se n = 4, ne esistono 16. Possiamo fermarci qui, ma è facile capire che potrei aumentare a dismisura il numero di coordinate e quindi passare a spazi a qualsivoglia numero di dimensioni. Il tensore sarebbe sempre e comunque di rango 2, dato che per descriverlo occorrono solo 2 indici.

A questo punto siamo interessati a vedere come il nostro tensore reagisce quando viene cambiato il sistema di riferimento. Ecco che la formula (3) diventa fondamentale, dato che lei ci diceva come venivano trasformate le coordinate di un vettore cambiando sistema di riferimento. Utilizziamola per i nostri due vettori la cui combinazione fornisce il tensore T^mn

A_y^m = ∑_r(∂y^m/∂x^r) A_x^r

B_yⁿ = ∑_s(∂yⁿ/∂x^s) B_x^s

dove r e s indicano i termini della sommatoria, mentre A_y e A_x, così come B_y e B_x sono le componenti dei vettori nei due sistemi y e x.

La composizione dei due vettori porta a scrivere:

A_y^m B_yⁿ = ∑_r(∂y^m/∂x^r) A_x^r  ∑_s(∂yⁿ/∂x^s) B_x^s

Ma il primo termine non è altro che il termine del tensore T nel sistema y

T_y^mn = ∑_r(∂y^m/∂x^r) A_x^r  ∑_s(∂yⁿ/∂x^s) B_x^s

Ordiniamo un pochino le cose (fidatevi... si può fare)

T_y^mn = ∑_rs(∂y^m/∂x^r)(∂yⁿ/∂x^s)A_x^r B_x^s 

La parte segnata in verde, però, non è altro che il nostro tensore T nel sistema x, ossia:

T_y^mn = ∑_rs(∂y^m/∂x^r)(∂yⁿ/∂x^s)T_x^rs                .... (4)           CONTROVARIANTE

La (4) ci dice come si trasformano le componenti di un tensore passando da un sistema a un altro. Ovviamente essa rappresenta un solo termine nel sistema y, ma la stessa relazione vale per ogni valore di m e n.

L'operazione che abbiamo fatto ha un nome molto particolare e viene chiamata trasformazione controvariante. Esiste anche un'altra trasformazione che prende il nome di covariante, sempre legata ai nostri tensori nei due sistemi di riferimento. Per scriverla portiamo gli indici in basso e invertiamo i gradienti, ottenendo:

T_mn(y) =∑_rs(∂x^r/∂y^m)(∂x^s/∂yⁿ)T_rs (x)       .... (5)            COVARIANTE

Ci sono vari modi per introdurre le coordinate covarianti e controvarianti, così come per utilizzarle nelle trasformazioni di coordinate (derivate di y rispetto a x o viceversa, ossia le classiche coordinate o quelle inverse ). Non vorrei, però, allargare troppo il discorso, dato che tutto ciò può essere trovato in rete e i passaggi veramente fondamentali e complessi ci aspettano. Magari Fabrizio potrebbe, se ha voglia, affrontare il discorso separatamente... io mi limito a una semplice definizione che riporto di seguito.

Componenti covarianti e controvarianti 

Cerchiamo di comprendere in modo molto semplice e senza tante formule matematiche la differenza tra componenti controvarianti e covarianti. Limitiamoci a uno spazio a due dimensioni e a due assi x¹ e x² (non necessariamente perpendicolare tra loro, ovviamente). Nella Fig, 9, in alto, inseriamo un vettore V e separiamolo nelle sue due componenti lungo gli assi, nel modo più normale e comune.

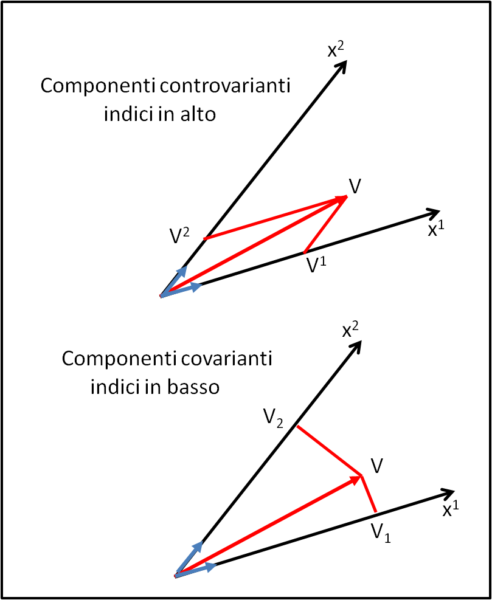
Bene queste due componenti sono dette CONTRO(varianti). Perché "contro"? Presto detto. Per misurare la lunghezza di un vettore dobbiamo riferirci a un versore unitario (vettori blu) e vedere quante volte è contenuto nel nostro vettore. Cosa succede se io aumento le dimensioni del versore unitario (l'unità è una nostra scelta)? Succede che le componenti del vettore diminuiscono il loro modulo. Se prima una componente valeva 4 versori unitari, raddoppiando quest'ultimo la componente diventa adesso 2. In poche parole, aumentando o diminuendo il valore della lunghezza del versore unitario, diminuisce o aumenta il valore della lunghezza della componente del vettore. Insomma andiamo sempre al contrario! Il vettore finale, comunque, pur cambiando le sue componenti sulla base dell'unità scelta, rimane sempre quello che è.

Immaginiamo, adesso, di usare un nuovo tipo di componenti dello stesso vettore (Fig. 9, in basso), utilizzando gli stessi assi, ma definendo come componente il prodotto scalare tra vettore e versore di un certo asse. Il prodotto scalare di due vettori è il prodotto dei moduli dei due vettori moltiplicato per il coseno dell'angolo compreso. L'angolo compreso è quello che è e quindi anche il coseno. Cosa succede, in questo caso, se aumento la lunghezza del versore? Semplice, deve aumentare anche la componente, dato che il vettore vale quello che è mentre il versore si ingrandisce e l'angolo resta lo stesso. Ovviamente avviene il contrario se lo diminuisco. Versore e componente vanno d'amore e d'accordo, e quindi sono CO(varianti).

Sono due tipi di componenti che danno luogo a trasformazioni di coordinate di uno stesso vettore o, più in generale, di un tensore. Ecco, perciò, due modi di scrivere le trasformazioni...

Ovviamente, nel caso che ci trovassimo di fronte ad assi cartesiani, i due tipi di componenti coincidono (il prodotto scalare dà proprio la coordinata  del punto di arrivo del vettore).

Queste trasformazioni di coordinate dei tensori che abbiamo cercato di costruire passo dopo passo (ricordiamoci che sono equivalenti) teniamocele molto strette. Adesso torniamo a concetti molto più banali (a prima vista) e, in particolare, al teorema forse più conosciuto e utilizzato: il teorema di Pitagora. Tuttavia, la vera differenza è che non siamo più in uno spazio euclideo e nemmeno nelle tre dimensioni.