Categorie: Relatività
Tags: delta di Kronecker Relatività Generale al microscopio tensore metrico teorema di Pitagora
Scritto da: Vincenzo Zappalà
Commenti:19
La relatività Generale al microscopio. 6: Da Pitagora al tensore metrico ***
Questo è l'ottavo articolo della serie "La Relatività Generale al microscopio"
Partendo dal teorema di Pitagora sul piano arriviamo a quello su uno spazio curvo, grazie al tensore metrico... le cose si complicano e le sommatorie si affollano.
Scriviamo il nostro caro Teorema di Pitagora per trovare la distanza ds nel piano x1, x2 (spazio a due dimensioni).
ds2 = dx12 + dx22
utilizzando, ormai, gli apici per determinare i vari assi coordinati abbiamo segnato in rosso l'effettiva operazione di elevazione al quadrato...
Se poi vogliamo trovare la distanza ds nello spazio a tre dimensioni (Fig. 10), dobbiamo applicare ancora una volta il Teorema e scrivere:
ds2 = ds2 + dx32
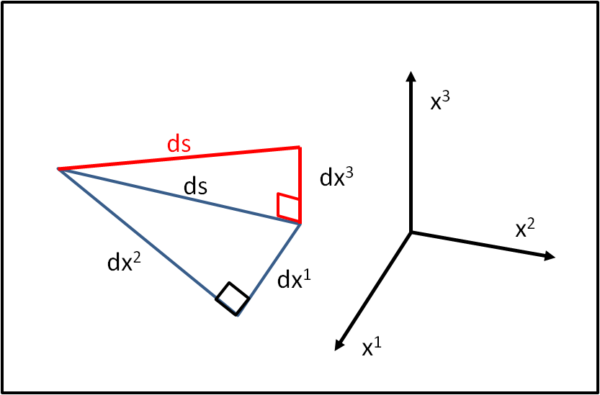
Che pasticcio di colori e di indici... crea solo una grande confusione... Proviamo allora a scrivere ds per esteso
ds2 = dx12+ dx22+ dx32
E, invece del quadrato che ci causa il numerino rosso, moltiplichiamo dxn per se stesso...
ds2 = dx1 dx1 + dx2 dx2 + dx3 dx3
Il ds può pure mantenersi il suo esponente dato che è chiaro che si riferisce al sistema x e possiamo scrivere il teorema di Pitagora in 3 dimensioni:
ds2 = ∑mdxm dxm
Una formuletta che ci permette di considerare quante dimensioni vogliamo... basta estendere la sommatoria a m sempre più grande. In poche parole, e non ridete se questi passaggi sono stati poco più che infantili, la formuletta ci permette di estendere il calcolo della distanza tra due punti a uno spazio a m dimensioni.
Tanto che ci siamo, divertiamoci ancora un poco...
La stessa formula di prima la posso anche scrivere in modo apparentemente inutile, ma che tale non sarà. Essa contiene solo i termini che moltiplicano un dx per se stesso, ossia dxm per dxm. Perché non tenere in conto anche i termini in cui le x di indice diverso si moltiplicano tra loro? Meglio scriverla direttamente:
ds2 = ∑mndxm dxn
E' sempre corretta? Nemmeno per sogno! Il teorema di Pitagora non tiene certo conto dei termini in cui dx1 moltiplica dx2 e via dicendo... Beh... possiamo migliorarla, moltiplicando il secondo membro per un certo fattore δmn, un fattore semplicissimo e molto "vigile", che dirige il traffico in modo da far rimanere la formula nell'ambito di correttezza del teorema del grande matematico greco. Come può fare? Banale:
δmn vale 1 (ossia dà il via libera) solo quando m = n, mentre δmn = 0 (ossia blocca il traffico) quando m≠ n.
A questo attento vigile è stato dato il nome di delta di Kronecker. La formula del teorema di Pitagora così costruita diventa perciò
ds2 = ∑mnδmndxm dxn
E' venuto il momento di utilizzare nuovamente la (1). Ancora una volta la possiamo scrivere, cambiando il nome alle coordinate:
dxm = ∑r (∂xm/∂yr )dyr .... (1a)
Attenzione! A questo punto cerchiamo di non sovraffollare le nostre formule con troppi segni di sommatoria e nella (1a) eliminiamo "visivamente" la sommatoria, pur sapendo che essa continua a esistere! D'altra parte l'indice r, per il fatto stesso di apparire, ci fa capire che stiamo sommando qualcosa con r ,che copre il numero di dimensioni considerate. La formula resta sempre un modo per descrivere una certo spostamento lungo una coordinata di un sistema x attraverso una sommatoria di gradienti relativi ciascuno a uno spostamento lungo gli assi del sistema y (siamo sempre nel caso della Fig. 7).
Forza e coraggio... e andiamo a sostituire la (1a) nella "nuova" formula del Teorema di Pitagora:
ds2 = ∑mnδmndxm dxn
ds2 = ∑mn δmn (∂xm/∂yr )dyr (∂xn/∂ys ) dys
Abbiamo lasciato la sommatoria su m e n, ma Einstein aveva preferito toglierla. Comunque sia, riscriviamo la formula in altro modo:
ds2 = ∑mn δmn(∂xm/∂yr ) (∂xn/∂ys) dyr dys
Sì, lo so ... è una formula decisamente molto complicata a causa delle sommatorie che intervengono, ma non fa che esprimere una "semplice" serie di trasformazioni di coordinate. Non solo, essa non è altro che il Teorema di Pitagora, scritto in modo "leggermente" diverso...
ds2 = ∑mn δmn(∂xm/∂yr ) (∂xn/∂ys) dyr dys
Tutta la parte rossa non è altro che un tensore (combinazione di vettori) e viene chiamato TENSORE METRICO gmn, da cui:
ds2 = gmn dyr dys
Questa formula diventa quella "normale" se si è in uno spazio piano, per il quale il tensore metrico si riduce a δmn. Definiamo in modo molto "rozzo", ma più comprensibile il significato profondo del tensore metrico. Esso non è altro che una correzione che bisogna applicare al teorema di Pitagora quando si passa da uno spazio piano a uno spazio curvo, una specie di "macchina" che ci permette di estendere il teorema di Pitagora a qualsiasi spazio a n dimensioni e, in particolare, a uno spazio a 4 dimensioni, di cui una è il tempo, ossia uno spaziotempo a quattro dimensioni.
In modo ancora più sintetico, il tensore metrico permette di calcolare la lunghezza di un arco di curva su uno spazio qualsiasi. Ciò è stato ottenuto, limitandoci allo studio delle trasformazioni di coordinate in un una zona estremamente piccola dove lo spazio può essere espresso in modo simile a quello piano. Una definizione non propriamente corretta, ma che in qualche modo dovrebbe aiutare a capire tutto ciò che è stato fatto. Abbiamo definito, attraverso uno studio LOCALE "piatto", le caratteristiche di qualsiasi trasformazione di coordinate su uno spazio curvo. In ogni punto si riesce a intervenire sapendo come agire per calcolare spostamenti e/o distanze infinitesime nell'intorno del punto.
Bene (si fa per dire) ... siamo riusciti a descrivere un tensore che compare nell'equazione di Einstein, quel fattore correttivo che, pur essendo stato ricavato attraverso uno studio locale, ci permette di agire per trasportare il tutto su uno spazio curvo. Einstein non usa gli indici m ed n, ma μ e ν, e si permette di agire sia su coordinate spaziale che temporali, ossia di agire non solo su uno spazio curvo ma su uno spaziotempo curvo.
Cerchiamo di dire le cose in modo un po' più tecnico, ma senza cadere in frasi matematicamente troppo elevate. Vogliamo descrivere la curvatura di uno spazio a n dimensioni. Consideriamo un piccolo spostamento del punto approssimando il tratto con una normale geometria piana o -meglio- quasi piana alla Minkowski. Scriviamo le trasformazioni delle coordinate che lo contraddistinguono durante il suo movimento. Ne segue che nel passaggio da un sistema inerziale a uno non inerziale deve sempre essere possibile trovare una trasformazione di coordinate per passare dall’uno all’altro e viceversa. il campo gravitazionale localmente può essere assimilato ad un sistema non inerziale, è quindi sempre possibile trovare una trasformazione di coordinate che porti da un sistema soggetto a campo gravitazionale ad un sistema di riferimento inerziale in cui il campo gravitazionale è trascurabile a livello locale. In questo intorno infinitesimo dell’evento quadridimensionale è quindi valida la teoria della relatività ristretta. Per far ciò è necessario poter cambiare il sistema di coordinate mantenendo comunque inalterata la distanza percorsa (così come capita per una distanza nel piano di Minkowski).
Una volta descritta questa trasformazione tra coordinate si può passare ad applicarla ai vettori. Il tensore metrico è un operatore che permette di tener conto di un movimento in uno spazio comunque curvo a n dimensioni tale da mantenere invariata la "distanza" percorsa. In parole ancora più semplici, il tensore metrico permette di descrivere la geometria locale di uno spazio a n dimensioni e, in particolare, dello spaziotempo a quattro dimensioni.
Lo sforzo enorme di tutte queste trasformazioni è riuscire a riprodurre ciò che è stato possibile nella relatività ristretta, ossia determinare una trasformazione che mantenga inalterata una certa distanza al cambiare del sistema di riferimento, anche passando a un sistema non inerziale, lavorando localmente in un ambito talmente ristretto tale da poter approssimare il tutto, fino a che è possibile, con la metrica tipica della relatività ristretta.
Abbiamo il correttore e cerchiamo di studiarlo meglio per poi poterlo applicare a uno spaziotempo curvo: le cose cominciano a complicarsi e si devono introdurre simboli diversi...






19 commenti
Scusi, riguardo alla formula:
"ds2 = δmn ∑mndxm dxn
Il delta è fuori dalla sommatoria, dato che sa già se alzare bandiera verde o bandiera rossa a seconda dei valori di m e di n e intervenire subito per annullare il termine della sommatoria in cui si moltiplicano termini con indici diversi."
siamo sicuri che possiamo portare fuori il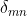 dal simbolo di sommatoria? Non è mica una costante, e anzi dipende proprio da m,n. O intendeva qualcos'altro?
dal simbolo di sommatoria? Non è mica una costante, e anzi dipende proprio da m,n. O intendeva qualcos'altro?
Appunto Franco, gli indici m e n gli dicono già se può essere 1 o 0. E' uno scalare che varia secondo m e n... Poteva anche essere messa dentro, ma la struttura della formula non cambia ed è quella seguita normalmente nella metrica. Il significato rimane lo stesso... Nel caso più semplice, lavorando prima della sommatoria si riduce alla formula del teorema di Pitagora...
ds2 = δmn ∑mndxm dxn
ds2 = 1 dx1 dx1 + 0 dx1dx2 + 0 dx2dx1 + 1 dx2dx2
Per ogni termine della sommatoria acquista il valore corrispondente, ossia quello che lo identifica nella matrice delle sue componenti. E' proprio un tensore di rango 2 su uno spazio a due dimensioni...
1 0
0 1
se ho capito bene la tua domanda...
Sai, Franco, le sommatorie tenderebbero ad aumentare e si è cominciato a eliminarle visivamente, ma esse restano attraverso la comparsa degli indici variabili. Questo è uno dei grandi problemi delle varie formule legate alla metrica curvilinea... Einstein ne ha levate ancora di più... In pratica si è creata una simbologia ad hoc, comprensibile se si ha veramente in mano la problematica. Nessun problema, quindi, a considerare quel fattore all'interno, dato che poi comparirà all'interno del tensore metrico.
Non starò ad insistere ulteriormente.
Scalare o no, un termine che dipende da m,n non può essere raccolto
in una sommatoria essendo dipendente da m,n. Così sembra che moltiplichi la somma, non i singoli
termini. Ma in ogni caso non va bene per me. Non ho mai visto un tipo simile di formalismo
Boh, non capisco.
va bene... come detto, se preferisci consideralo pure all'interno della sommatoria...
Le notazioni sono quelle usate da Einstein. Il succo è che a seconda del termine della sommatoria il valore del delta prende il valore corrispondente . Non le ho inventate io queste notazioni, di sicuro...
scusi le risposte a singhiozzo, ma purtroppo il tempo è quello che è. Mi risultata che Einstein abbia introdotto dele notazioni per eliminare le sommatorie, con le sue note convenzioni:
https://it.wikipedia.org/wiki/Notazione_di_Einstein
non per portare fuori dal simbolo di sommatoria cose come il delta di K. Allora sì lo scrittura avrebbe senso, se scritta così:
tenendo conto appunto della sua convenzione:
Quando un indice si presenta due volte in un termine di un'espressione occorre sommare rispetto ad esso, salvo il caso che sia esplicitamente indicato il contrario.
invece che così:
ds2 = δmn ∑mndxm dxn
Ok, Ok... intendevamo la stessa cosa... ci vuole poco annullare la sommatoria che avevo mantenuto per cercare di semplificare...
Scusa, ad un certo punto compaiono gli apici s, cosa sono?
cara Maria Grazia,
sono gli indici delle due sommatorie delle formule (1a) applicata a xm e xn , ossia:
dxm = ∑r (∂xm/∂yr )dyr
dxn = ∑s (∂xn/∂ys )dys
che, però, vengono tralasciate, secondo quanto detto nel testo:
A questo punto cerchiamo di non sovraffollare le nostre formule con troppi segni di sommatoria e nella (1a) eliminiamo "visivamente" la sommatoria, pur sapendo che essa continua a esistere! D'altra parte l'indice r, per il fatto stesso di apparire, ci fa capire che stiamo sommando qualcosa con r ,che copre il numero di dimensioni considerate.
Ovviamente, la stessa cosa vale per la sommatoria con indice s. Sai, sono solo indici, scelti con lettere a caso, importanti per far capire che si stanno eseguendo delle sommatorie separate...
Grazie per la pronta risposta e vivissimi complimenti per il blog, utilissimo e chiaro anche per chi come me, che ho superato gli ottanta, è un po' arrugginito in matematica e fisica.
carissima Maria Grazia,
è un vero piacere per me esserti utile. Alla nostra età dobbiamo far girare le rotelle al massimo: è l'unico modo per non fare addormentare il nostro computer di bordo. Quando è occupato non pensa a fare danni altrove!
E, mi raccomando, il TU è d'obbligo tra noi
Chiedo scusa, ma ho un'altra domanda. Perché siamo partiti dal teorema di Pitagora per arrivare al tensore metrico? Sarebbe stato possibile partire da un altro teorema o da un'altra figura geometrica?
cara Maria Grazia,
il teorema di Pitagora è quello che meglio determina la differenza tra uno spazio piano e uno curvo. Il tensore metrico permette di renderlo fruibile in qualsiasi spazio. Teniamo anche conto che il teorema di Pitagora è proprio legato al prodotto di due vettori (vedi come esempio il prodotto scalare) e quindi è perfetto per la definizione di un tensore. Ricordiamoci che si fa riferimento proprio al teorema di Pitagora "modificato" quando si parla di minimo percorso e di distanza invariante nello spazio di Minkowski (riferimento piano, ma con assi non ortogonali e legame spaziotemporale).
Grazie Vincenzo, sei stato molto chiaro come al solito.
P.S. Preciso che l'account da cui scrivo è a nome di mia moglie appunto Maria Grazia, io sono Michele.
Ops... Michele! Comunque un caro saluto anche a tua moglie!!
Caro Vincenzo
a quando la
LA RELATIVITÀ GENERALE AL MICROSCOPIO. 7?
Scusa la mia intrusione ma è molto interessante
Michele
Tra poco Michele... tra poco

e grazie...
Richiesta chiarimento su ds2 = ∑mn δmn(∂xm/∂yr ) (∂xn/∂ys) dyr dys che nel testo ha una parte in rosso, ma nei commenti i colori, gli indici e gli apici vengono inibiti.
Mi sembra di capire che ds2 non è la distanza al quadrato tra due punti, ma solo una componente della distanza. Però compaiono DUE indici r s in dyr dys, che non vengono sommati né in m, né in n . Che componente è? O non è una componente? In ds2, ci vorrebbero degli indici r,s?
Mi spiace Giangiacomo, ma meglio di così non riesco a spiegare. Avevo detto, fin dall'inizio, che era un argomento ostico e che per entrare nei dettagli più fini era necessaria una trattazione di matematica superiore che in questo blog non è plausibile. Cerca du libri professionali o su testi universitari... abbi pazienza.