Questo è il decimo articolo della serie "La Relatività Generale al microscopio"

Vi sono vari modi per definire la "curvatura". Solitamente quando si parla di curvatura si intende la curvatura di una linea nello spazio a due o a tre dimensioni. Abbiamo anche parlato della curvatura di una superficie, come ad esempio quella sferica e abbiamo visto come le regole della geometria euclidea non siano più valide. In particolare, non vale più il teorema di Pitagora ed esso deve essere corretto attraverso il nostro "amico" tensore metrico. Adesso, vediamo come una curvatura di uno spazio a 4 dimensioni influisca su un vettore che si sposti su di esso.

Prendiamo, perciò, un vettore di modulo costante e applichiamolo su un quadratino di superficie abbastanza piccolo da essere rappresentato da un piano (le sue trasformazioni al cambiare del sistema di riferimento le abbiamo analizzate a fondo così come le sue derivate). Per ora, limitiamoci a rappresentare una superficie a due dimensioni, immersa in tre dimensioni, e spostiamo il nostro vettore cercando di mantenerlo sempre uguale oltre che in modulo, anche in  direzione.

In Fig. 11 (a sinistra) rappresentiamo la nostra superficie come un piano. Il vettore rosso si sposta parallelamente a se stesso in altri piccoli quadratini e quando torna indietro, al punto di partenza coincide esattamente con quello di partenza.

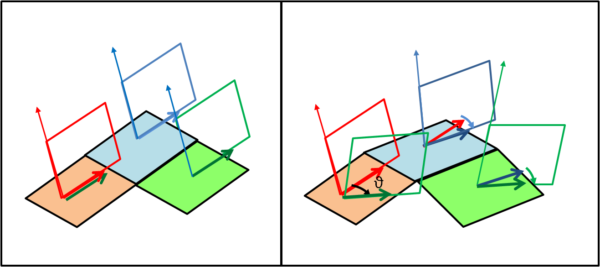
Rappresentiamo, adesso (a destra), una superficie curva in cui i quadratini approssimino le varie parti della superficie. Muoviamo il vettore rosso nel quadratino azzurro. Le cose non tornano, dato che il vettore si trova "fuori dalla superficie" Nel punto di applicazione consideriamo la perpendicolare al quadratino azzurro e ruotiamo il vettore rosso fino a farlo adagiare sulla superficie . Fatto questo, spostiamolo nel quadratino verde. Nuovamente il vettore si viene a trovare "sospeso" e deve essere ruotato facendo riferimento alla perpendicolare nel punto di applicazione.

Non ci resta che riportarlo pari pari nel quadratino di partenza. Bene, dopo tutte le piccole rotazioni avvenute nei vari quadratini, per aver dovuto adagiarlo sulla loro superficie piana, il vettore finale verde NON coincide assolutamente più con quello di partenza. Questo valore dello spostamento indica proprio la curvatura della superficie ed è stata ottenuta attraverso il viaggio (di andata e ritorno) di un vettore. Si intuisce già, però, come la curvatura dipenda anche molto dalla lunghezza del viaggio...

E' meglio fare un altro esempio di quanto abbiamo cercato di spiegare. In Fig. 12 consideriamo un qualsiasi linea curva su uno spazio piano.

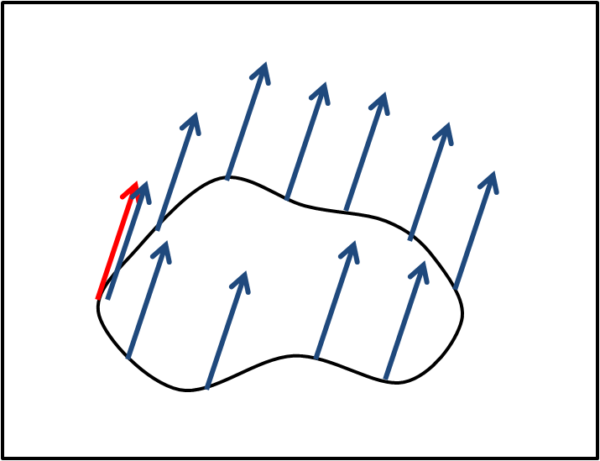
Muoviamo il vettore rosso lungo questa curva, mantenendo modulo e direzione. Tornando a "casa", di quanto è cambiato il vettore? Di niente, la sua deviazione è stata nulla. Nulla è , quindi, anche la curvatura (non confondiamo la linea curva, descritta dal punto di applicazione del vettore, con lo spazio curvo!)

Consideriamo adesso un cono (facile da costruire partendo da un settore di circonferenza). Il cono ha una superficie curva. Cerchiamo di misurare la sua curvatura con la strategia adottata precedentemente? Molto facile. Prendiamo un paio di forbici e tagliamo il cono lungo una sua generatrice in modo da ottenere la superficie piana di Fig. 13.

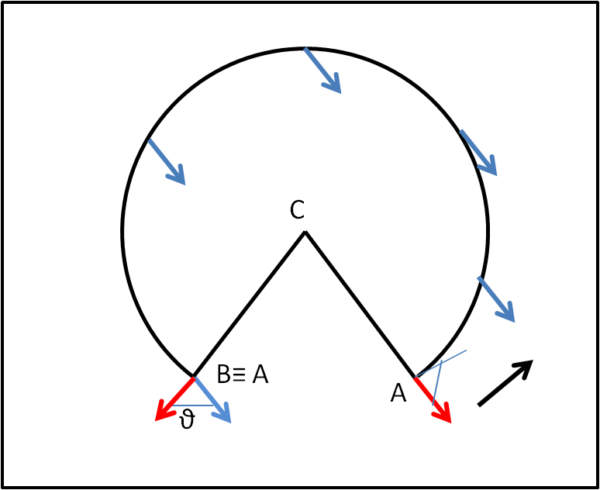
Attenzione, però: la linea AC è separata dalla linea CB, ma esse devono coincidere quando ricostruiamo il cono. Il che vuol dire che ciò che capita rispetto alla linea AC capita anche rispetto alla linea CB, una volta tornata al suo posto sul cono.

Prendiamo un vettore rosso diretto proprio lungo AC e trasliamolo parallelamente a se stesso lungo il bordo del cono fino a farlo arrivare in B. Possiamo dire che che il vettore è diretto lungo la direzione CB? Assolutamente no. Esso forma un certo angolo. Accidenti, ma sappiamo che AC e BC coincidono nel cono "ricostruito" e quindi vuol dire che il vettore è tornato al punto di partenza ruotato rispetto a quello originale (che è quello rosso sempre diretto da A o da B verso C). Pur muovendosi in modo parallelo, alla fine non è più lo stesso! La superficie conica è una superficie curva e l'angolo formato tra il vettore partenza e quello di arrivo indica che tipo di cono abbiamo per le mani, ossia la sua curvatura.

Molto importante è anche la lunghezza del percorso eseguito. Consideriamo una sfera (Fig. 14) e muoviamoci lungo un meridiano, eseguendo le piccole rotazioni già viste nella Fig. 12,

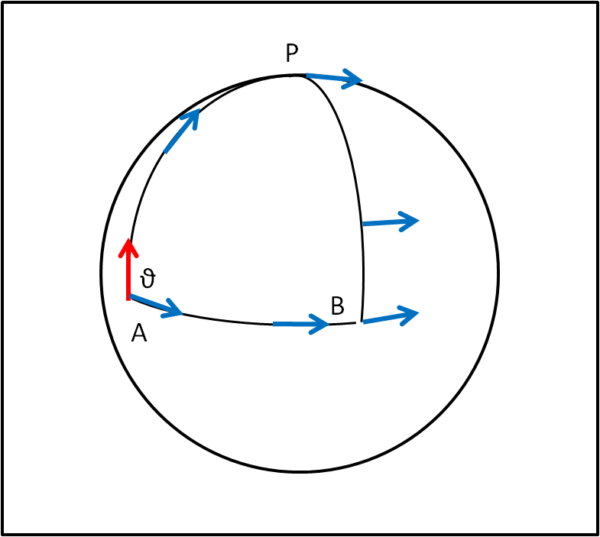
Giunto al polo il vettore prende un altro meridiano mantenendo sempre la stessa direzione, ma continuando a eseguire le piccole rotazioni. Giunto infine sull'equatore non gli rimane che tornare al punto di partenza. Sorpresa! esso si ritrova girato di ben 90°. Provate a farlo muovere ancora di più, andando dall'equatore al polo e poi continuare sullo stesso meridiano fino a farlo arrivare all'equatore. Poi, lungo l'equatore, percorrendo metà di esso per tornare al punto di partenza. Bene, la rotazione è diventata di 180° (Fig. 14a).

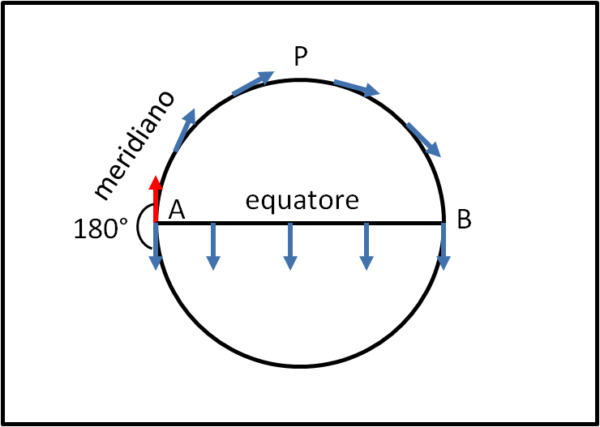
Bisogna quindi anche tener conto del percorso effettuato o -se preferite- dell'area racchiusa dalla curva seguita dal vettore.

Sappiamo come si trasformano i vettori e le loro derivate, ma adesso sappiamo anche come quantificare la curvatura e agire di conseguenza quando si vuole farli relazionare sotto forma di tensori.