Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Il "nostro" amico momento angolare ha deciso di partecipare in prima persona a una nuova specialità olimpica. il sollevamento pesi a... metà

Conosciamo molto bene il momento angolare e, soprattutto, sappiamo quanto sia "conservativo". In poche parole, cerca di ribellarsi al meglio a ciò che vuole disturbarlo.

La conservazione del momento angolare è una delle leggi fisiche più importanti e, giustamente, ne abbiamo parlato spesso. Questo fatto ci fa pensare a una nuova specialità olimpica: il sollevamento pesi "a metà". Ma, andiamo con calma e ricordiamo come come nasce la conservazione del momento. Partiamo dalla conservazione della quantità di moto e poi trasferiamo il tutto su un sistema rotante.

La quantità di moto è uguale al prodotto tra la massa del corpo e la sua velocità. E', quindi un vettore.

q = mv

Cosa è necessario fare per modificarlo? Non possiamo usare la massa m, dato che, almeno in fisica classica, essa è una proprietà intrinseca del corpo. L'unica possibilità è, quindi, quella di cambiare la velocità, ossia imporre una sua variazione. Ne segue che

dq/dt = m dv/dt

Ma sappiamo che dv/dt non è altro che l'accelerazione a, ossia:

dq/dt = m a

Ma Newton dice anche che

F = ma

Quindi:

F =  dq/dt = m dv/dt

In altre parole, per variare la quantità di moto è necessario imporre una forza esterna F. Tuttavia, il corpo cerca di contrastare questa variazione  e lo fa tramite la sua massa (inerzia). La formuletta precedente ci dice che più cresce la massa del corpo  e più forza ci vuole per impartirgli una certa variazione di velocità rispetto a quella costante che lui vorrebbe mantenere:

dv/dt = F/m

Un discorso del tutto analogo si può fare per i moti rotatori, Al posto della quantità di moto si deve inserire il momento angolare L e, al posto della forza, il momento della forza M. Dire la parola "momento" significa eseguire un prodotto vettoriale tra un vettore e la sua distanza r da un certo punto fisso O.

Nel caso che il vettore sia proprio la quantità di moto, si ha:

L = r Λ q =  r Λ mv  = m r Λ v

Non dimentichiamo, ovviamente, che il prodotto vettoriale è ancora un vettore la cui direzione è perpendicolare al piano dei due vettori e il verso segue la celebre regola della mano destra o della vite.

Passiamo al suo modulo (supponendo per semplicità che i due vettori siano perpendicolari tra loro) e ricordiamo che:

v = r ω      (ω è la velocità angolare)

Da cui:

L = m r² v  = I ω        (I = momento d'inerzia)

Se il corpo non è puntiforme il valore di I cambia a seconda della forma, ma resta, comunque, uno scalare caratteristico del corpo.

Come si vede per ottenere L da q, abbiamo solo sostituito la massa con il momento d'inerzia e la velocità lineare con quella angolare.

Cerchiamo adesso di cambiarlo, ossia di costruire una variazione dL/dt

dL/dt = m d(rΛ v)/dt = m dr/dt Λ v + m r Λ dv/dt = m v Λ v + m r Λ a = r Λ ma = r Λ F = M

dove ovviamente il prodotto vettoriale tra due vettori uguali è zero e dv/dt è l'accelerazione

In altre parole, per far variare un momento angolare L bisogna applicare il momento M di una forza. Passando al modulo:

M = r F

Se r è più grande, basta una forza minore e viceversa. Non per niente, per aprire un cancello chiuso molto pesante (che ha momento angolare uguale a zero), è preferibile applicare la forza il più lontano possibile dalla cerniera!

Bene, abbiamo dato una piccola rinfrescata (per saperne di più andate all'articolo già menzionato prima oppure acquistate il ben più generale  libro "La Fisica addormentata nel Bosco").

Non ci resta che passare al sollevamento pesi, avendo sempre presente la... precessione degli equinozi. No, non sto scherzando, le due cose sono del tutto equivalenti. In entrambi i casi si cerca di cambiare un momento angolare e lui si ribella come può.

In Fig. 1  abbiamo un bilanciere professionale, ossia quelli usati alle olimpiadi. Il peso totale è equidiviso tra i due dischi esterni e possiamo considerare nullo il peso dell'asta che li unisce (tuttavia, essa deve essere molto resistente per non spaccarsi a metà durante l'azione atletica).

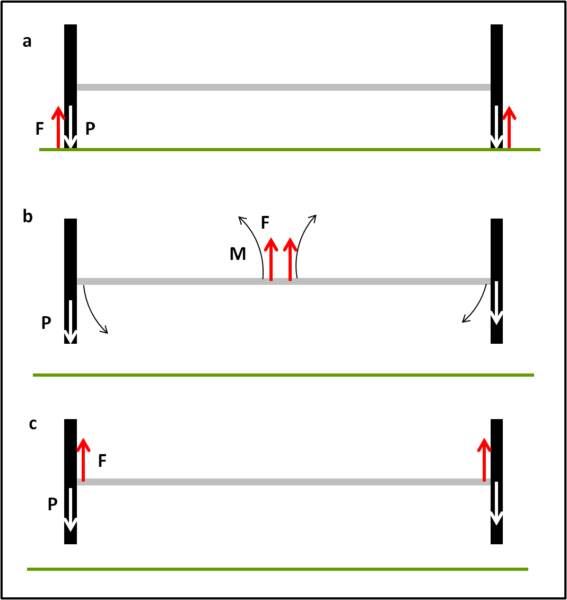
Finché il bilanciere è a terra (a), si ha equilibrio, dato che alle forze peso dei due dischi si contrappongono le forze di reazione del terreno. Come fare a sollevare il  bilanciere? In linea di principio, basta pensare che le due forze peso dei dischi possono essere traferite nel baricentro del bilanciere e quindi le mani dell'atleta devono impartire in quel punto una forza uguale e contraria.  Le due mani dell'atleta si accostano al baricentro ed esercitano insieme una forza uguale e contraria (b). Perfetto? Beh... non è tanto conveniente mettere le mani vicino al baricentro. dato che le due forze peso sono applicate, in realtà, a una certa distanza dalle  mani e, di conseguenza, tendono ciascuna a creare una coppia di forze con le reazioni uguali e contrarie delle mani. Coppia di forze vuol dire in pratica applicare una forza ai due dischi e dar luogo a un momento della forza M; tale momento non è altro che la forza peso moltiplicata per la distanza tra disco e mano.  Tendenzialmente questa doppia azione potrebbe portare alla rottura dell'asse del bilanciere, ma se questo è perfettamente rigido sa come rispondere alle due sollecitazioni. Comunque, è difficile equilibrare la coppia di sinistra con quella di destra: basta una leggera diversità tra le distanza dai dischi  per causare uno sbilanciamento e l'addio a una  posizione perfettamente statica.

Conviene perciò ridurre queste coppie, ossia i momenti delle forze peso, e portare le mani il più vicino possibile ai dischi (c). Se riuscissimo a fare coincidere punto di applicazione della forza peso con punto di applicazione della forza della mano, uguale e contraria, otterremmo le condizioni ideali per una stabilità finale. E questo è proprio quello che gli atleti cercano di fare.

Immaginiamo pure di aver vinto la medaglia d'oro e di voler tentare con uno sport simile, ma estremamente più complicato: il sollevamento pesi "a metà". In altre parole, prendiamo il nostro bilanciere e tagliamolo letteralmente a metà.

La gara è più meno simile, ma abbiamo un attrezzo con un solo disco. Beh... direte voi: "Cambia ben poco, anzi, usando entrambe le mani, potrei sollevare lo stesso peso di prima anche se concentrato in un solo disco. Basta metterle entrambe vicinissime al peso". Eh no! Sarebbe troppo facile! Le mani sono obbligate a restare vicino all'estremità senza peso. Le varie categorie impongono lunghezze diverse dell'asse del manubrio e, inoltre, vi sono due livelli di difficoltà: con entrambe le mani e con una mano sola. Iniziamo dal livello più basso, come mostra la Fig. 2a.

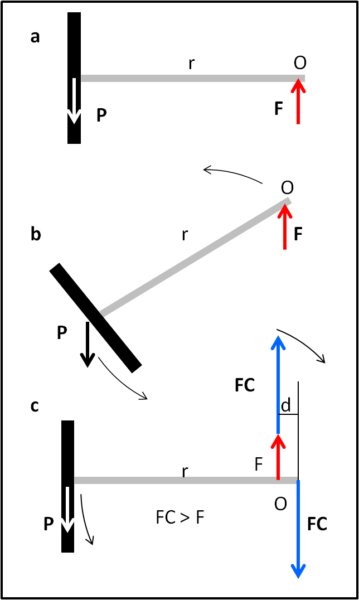
Tutto ciò che si può fare é reagire con una forza F applicata nel punto O, uguale e contraria alla forza peso P del disco (a). Va bene, abbiamo reagito alla forza peso, ma basta? No, assolutamente no, perché questa volta la coppia, che scaturisce dall'aver imposto una distanza r tra il disco e la mano, deve essere controbilanciata, altrimenti niente vieta al bilanciere di ruotare il disco verso terra (b). Potendo usare le due mani, anche se vicine tra loro e distanti dal disco, è possibile sollevare l'asta verso l'alto con una mano e spingere verso il basso con l'altra mano. In tal modo si ottiene una coppia che può annullare quella del disco. Tuttavia, il braccio tra le due forze FC da imporre, ossia tra le due mani, è molto piccolo. Per bilanciare la coppia dovuta a F e P, è necessario aumentare di molto entrambe le forze delle due mani. Una, poi, deve sommare questa forza FC a F che gli aveva permesso di non far cadere a terra tutto il bilanciere.  E questo è solo il primo livello...

Nel secondo livello, una sola mano deve fare tutto: tenere sollevata l'asta e imprimere una coppia con un braccio cortissimo. Non conosco bene la fisiologia della mano, ma temo che questa operazione sia decisamente difficile se non impossibile per un uomo (e poi dipende tutto dal peso del disco, ovviamente).

Siamo così sicuri che non ci sia niente di meglio da tentare? No, c'è eccome... La forza P tende a far ruotare tutto il sistema e, da come viene segnato in figura, lo fa ruotare in verso antiorario. Ciò vuole anche dire imprimere un momento di una forza, ossia una certa rotazione e quindi un certo momento angolare N diretto verso di noi. Chi fa cadere il disco è quindi proprio questo momento angolare. Tuttavia, possiamo cercare di agire sul disco e modificare il suo momento angolare che era nullo. Cosa possiamo fare? Banale, prima di  sollevare il bilanciere, l'atleta impone una rotazione molto rapida al disco, ossia gli regala un momento angolare L che va verso destra (Fig. 3).

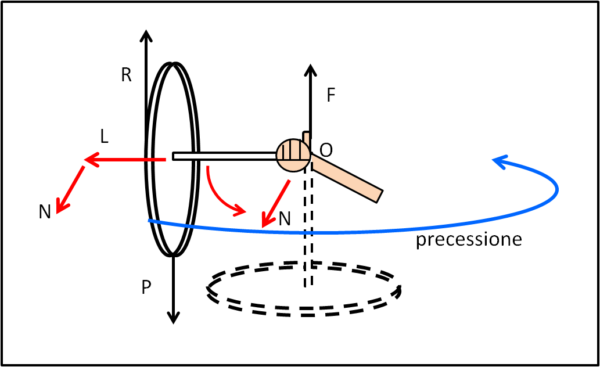
Poi solleva il tutto.  L si vede "disturbato" dal momento angolare N dovuto alla caduta del disco, ma cerca con tutte le sue forze di conservarsi, ossia di mantenere una certa velocità angolare costante. Non può fare miracoli, e non gli rimane che modificare istante per istante la sua direzione che si combina con quella del momento N. Ne segue che il disco oltre a ruotare intorno al proprio asse è costretto a spostarsi per accontentare N, ossia a precedere. In poche parole la rotazione riesce a tenere sollevato il disco. A questo punto, l'atleta deve solo evitare che il tutto cada per terra e quindi una sola mano gli basta e avanza! Deve anche avere l'accortezza di accompagnare, con il braccio e/o il corpo, la precessione, facendo magari finta di farsi vedere sia a sinistra che a destra...

Un esimio professore universitario riesce benissimo, malgrado l'età, a tenere sollevato un peso non  indifferente...

Poi, ovviamente, il disco rallenta la rotazione attorno al proprio asse e il bilanciere tende a cadere, ma ormai la medaglia d'oro non gliela toglie più nessuno!

Ancora più evidente risulta l'intera faccenda se appendiamo il mezzo bilanciere a un filo appeso al soffitto. Ovviamente, il mezzo bilanciere cade verso terra, ma il filo riesce a farlo stare sollevato. Se il disco, però, ruotasse, tutto lo strumento inizierebbe a ruotare perpendicolarmente alla direzione del filo (come nel caso del sollevatore del peso). Allego  un breve filmato che mostra molto meglio di tante parole quello che succede.

Bene, non vi ricorda esattamente ciò che fa una trottola? essa tende a ruotare attorno a un asse, ma la forza di gravità tende a farla cadere da un lato, cosicché inizia il celebre moto di precessione. La Terra è una trottola magnifica e subisce la precessione degli equinozi con  l'aggiunta che essa tende sempre a... "cadere" (andare verso il piano dell'eclittica), ma non esiste frizione che riesca a diminuire la rotazione attorno al proprio asse

Se, poi, manteniamo la rotazione costante otteniamo un giroscopio che riesce a segnalare qualsiasi disturbo possa far "precedere" la trottola.

Il giroscopio, infatti, è un dispositivo rotante che, per la conservazione del momento angolare, tende a mantenere il suo asse di rotazione orientato in una direzione fissa. Esso fa girare una specie di trottola, che continua imperterrita a girare fino a che qualche coppia esterna cerchi di farla "cadere" e allora si inserisce il moto di precessione.

Abbiamo seguito una trattazione estremamente semplificata che spero riesca, comunque, a far capire il concetto di fondo. Avevamo già trattato la precessione terrestre e spero che uno più uno faccia veramente due o anche qualcosa di più...