Categorie: Matematica
Tags: esponente logaritmo in base 10 potenze radici
Scritto da: Vincenzo Zappalà
Commenti:27
12. Logaritmi a gogò **
Iniziamo con una funzione che dovrebbe essere ben nota a tutti gli appassionati di astronomia, dato che si lega strettamente alle magnitudini stellari. La sua importanza è, però, decisamente superiore e il suo utilizzo vastissimo in tutti i campi della Scienza. Introdurremo quello in base 10, ma in seguito conosceremo anche quello che ha per base uno dei “magici” numeri della matematica.
Ripassiamo le potenze e le radici
Consideriamo una potenza di base a e di esponente b. Il risultato sia n
ab = n …. (1)
se b fosse uguale a 2, saremmo di fronte a un quadrato. L’operazione inversa del quadrato è la radice quadrata. A parole: la radice quadrata di n è uguale al numero il cui quadrato è n, ossia:
se il quadrato di a è n
a2 = n
la radice quadrata di n è a
a = n1/2
a è proprio il numero il cui quadrato è n.
La stessa definizione si può estendere alla radice cubica.
Se a3 = n, allora la radice cubica di n è quel numero a il cui cubo è n, ossia:
a = n1/3
Che l’operazione di radice sia l’inverso dell’elevamento a potenza può anche essere dimostrato direttamente:
(a3)1/3 = a3∙1/3 = a1 = a
Ossia eseguendo su un numero a prima il cubo e poi la radice cubica ottengo sempre il numero a (ricordate le proprietà delle potenze…).
Esiste, ovviamente, anche la radice b-esima di un numero n. Essa non è altro che un numero a tale che elevato alla b-esima potenza dia il numero n.
In termini matematici:
se
ab = n (potenza b-esima di a)
allora:
a = n1/b (radice b-esima di n)
Vale sempre, ovviamente:
(ab)1/b = a
Insomma tante parole e tante formulette per dimostrare che la radice b-esima è l’operazione inversa dell’elevamento alla b-esima potenza.
In generale, però, teniamo conto che, in fondo, anche l’operazione di estrazione di una radice b-esima è un elevamento a potenza. Infatti non è altro che elevare una base a un esponente minore di uno. Se l’esponente fosse negativo potremmo, invece, scrivere la potenza al denominatore.
Ricapitolando:
ab = n (b > 1 elevamento a potenza, b < 1 estrazione di radice b-esima)
a-b = 1/ab = 1/n (tanto per non dimenticare…)
Chiarito il concetto di radice b-esima o ennesima o quello che volete (2 e 3 sono i casi più usati che portano alla radice quadrata e a quella cubica), possiamo tranquillamente passare alla definizione di logaritmo.
Logaritmo: nome difficile per un concetto facile
Prima di partire con la descrizione di qualcosa che sembra apparentemente una creazione matematica fine a se stessa, fatemi dire che la Natura ama i logaritmi. E' un dato di fatto che molti fenomeni dell’Universo riescono a essere descritti solo facendo uso dei logaritmi. Non prendeteli in antipatia, quindi, e cercate di capirli a fondo perché la loro importanza è estremamente pratica. Comunque, ne parleremo ancora. Per adesso basta mostrare una figura ben nota a tutti: la spirale logaritmica. Quante manifestazioni della Natura la seguono? Provate a pensarci, andando dalle piccole lumache agli uragani e alle galassie (ne abbiamo ampiamente parlato in QUESTO articolo e nei link ad esso collegati)
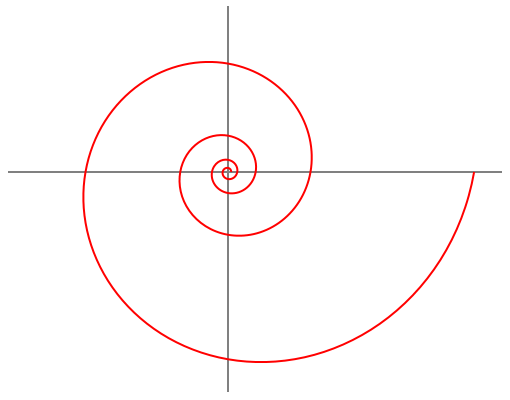
Finora abbiamo analizzato solo il numero su cui si svolge l’operazione di elevamento a potenza e la sua inversa, ossia la radice. Vogliamo occuparci, adesso, anche dell’esponente, ossia proprio di quel numero b, che dice quante volte un numero a va moltiplicato per se stesso nella (1)?
Chiamiamo logaritmo di un numero n l’esponente a cui bisogna elevare a per ottenere n. Il numero a prende il nome di base del logaritmo, dato che è quello che subisce l’operazione di elevamento a potenza
Se
ab = n
il logaritmo in base a di n si indica:
loga n = b …. (2)
Qualsiasi base andrebbe bene, ma, in pratica, ne sono normalmente utilizzate due. Tralasciamo quella più complicata (per adesso, almeno) e consideriamo come base a il numero 10. La (1) diventa:
10b = n
Il che vuole anche dire che il logaritmo in base 10 di n è proprio b e la (2) si scrive:
log10 n = b …. (3)
Perché si è preso come base proprio il numero 10? Perché noi usiamo il sistema decimale e quindi è estremamente utile usare il 10 come base di riferimento. Per capire la scelta del dieci (non fatta da tutti i popolo, però) guardate la Fig. 35 che mostra la più antica “calcolatrice” matematica usata dall’uomo e avrete subito la risposta.
La comodità del numero 10
Sapendo già qual è la base dei nostri logaritmi, non la scriviamo più, ma sappiamo che c’è. Proviamo a fare qualche logaritmo di numeri semplici:
log 10 = 1
Infatti, qual’é l’esponente a cui bisogna elevare 10 per ottenere proprio 10? Facilissimo: il numero 1, ossia:
101 = 10
Proseguiamo...
log 100 = log (102) = 2
Infatti, qual è l’esponente che bisogna dare a 10 per ottenere 100? Altrettanto facile: il numero 2. Ossia:
102 = 100
Continuiamo pure…
log 1000 = 3
log 10000 = 4
log 100000 = 5
E così via…. (in pratica, basta contare il numero degli zeri per avere il risultato, o -meglio ancora, basta contare il numero delle cifre della parte intera del numero e diminuire di uno: 1000 ha quattro cifre, quindi il logaritmo è 3; e via dicendo. Attenzione che stiamo considerando solo numeri interi...).
Quanto vale il logaritmo di 1? Qui le cose diventano leggermente più complicate, ma non di molto.
Ripetiamo l’operazione a parole. Qual è l’esponente a cui bisogna elevare 10 per ottenere 1? Non è poi così difficile. Esso può essere solo 0, dato che sappiamo bene che qualsiasi numero elevato a zero dà uno e, quindi, lo stesso deve capitare anche per 10. Possiamo scrivere:
100 = 1 e quindi:
log 1 = 0
Tutto bene fin qui? OK.
Attenzione: i risultati sono stati ovvi fino ad adesso perché abbiamo considerato numeri interi potenze di 10 (proprio la base del logaritmo). Ben diverso sarebbe stato il calcolo se avessi preso un numero qualsiasi. Ad esempio:
log 20 = 1.301
log 357 = 2.553
Come ho fatto? Beh … è stato "abbastanza" facile. La parte intera del logaritmo è uguale al numero delle cifre del numero scelto meno una: 20 ha due cifre quindi il logaritmo deve essere 1. …; 357 ha tre cifre, quindi il logaritmo deve essere 2. …. (come già visto precedentemente).
E la parte decimale? Lasciamo stare. Esistono delle tabelle apposite, ma ormai basta avere una calcolatrice e non vi sono problemi. Torniamo a cose più serie…
Riflettiamo un attimo. Abbiamo visto che al decrescere del numero decresce anche il logaritmo:
1000 --> 3; 100 --> 2; 10 -->1. Quando arriviamo al numero 1 si ha che il logaritmo diventa zero, ossia 1 --> 0. Cosa succede se il numero di cui vogliamo fare il logaritmo diventa più piccolo di 1? Beh… non è difficile rispondere: deve diventare più piccolo di 0, ossia negativo. Vogliamo fare una prova? Prendiamo, ad esempio, il numero 0.01, ossia 1/100.
log 0.01 = log(1/100) = ? …. (4)
No, non spaventiamoci… sappiamo che scrivere 1/100 vuole anche dire scrivere 1/102, ma sappiamo anche che quando vi è una potenza al denominatore si può portare al numeratore cambiando di segno all’esponente, ossia:
1/100 = 1/102 = 10-2
La (4) diventa:
log 1/100 = log 10-2
ma adesso non è difficile rispondere alla solita domanda: “Qual è l’esponente a cui devo elevare 10 per ottenere 0.01 (ossia 1/100 o anche 10-2)”. La risposta è ovvia: -2.
Senza ripeterci troppe volte, possiamo facilmente dire anche che:
log 0.1 = log(1/10) = log(10-1) = - 1
e, analogamente:
log 0.001 = - 3
log 0.0001 = - 4
log 0.00001 = - 5
E’ facile dedurre che se il numero decresce sempre di più il logaritmo diventa sempre più grande ma con segno negativo
Possiamo infatti continuare
log(10-100) = 0.000000000…….00000001 (0 virgola 99 zeri e poi 1) = -100
log (10-10000000) = 0.000000000…….000000001 (0 virgola 9999999 zeri e poi 1) = -10000000
non fatemi andare avanti…
Non "limitiamoci" e passiamo ai limiti
E’ più che chiaro che se scelgo un valore del numero sempre più piccolo (dato un numero ε piccolo a piacere posso sempre trovare un numero più piccolo di lui) il suo logaritmo è un numero (con segno negativo) sempre più grande (dato un numero M grande a piacere esiste sempre un logaritmo più grande di quel numero). Da quanto scritto non ho fatto altro che descrivere il limite del logaritmo di un numero quando il numero tende a zero, ed esso è - ∞.
Conoscendo ormai le funzioni posso chiamare x il numero e y il suo logaritmo, ossia:
y = f(x) = log x
La y è una funzione di x. L’operazione che svolge la funzione (ossia la famosa macchina) è quella di calcolare il logaritmo di x. Da quanto detto prima:
limx→0 (y) = limx→0 (log x) = - ∞
A parole, Il limite del logaritmo di x, per x che tende a 0, è uguale a - ∞
Ormai, abbiamo introdotto una funzione e possiamo quindi cercare anche il suo limite per x che tende a infinito.
Abbiamo visto che all’aumentare di x, aumenta anche il suo logaritmo y. Rivediamolo…
log 103 = log 1000 = 3
log 104 = log 10000 = 4
log 105 = log 100000 = 5
………………..
log 1020 = log 100000000000000000000 = 20
ecc., ecc.
Ossa, al tendere all’infinito del numero anche il suo logaritmo tende a infinito!
Possiamo quindi scrivere
limx→∞ (y) = limx→∞ (log x) = ∞
In parole povere, abbiamo descritto la funzione logaritmo. Lo faremo per molte altre funzioni e sarà sempre più divertente, dato che potremo sceglierle più o meno strane. Prima però, riflettiamo ancora un po’ sul logaritmo in base 10.
L’abbiamo analizzato nell’intervallo della x che va da 0 e + ∞. Che cosa capita per valori di x minori di zero? Ossia, che risultato abbiamo se inseriamo nella nostra funzione y = log x valori di x negativi?
Meglio ancora: è possibile ottenere un risultato? Assolutamente no. La definizione di logaritmo dice:
10y = x
Potete tentare tutti i trucchi che volete ma non troverete mai un esponente y che serva allo scopo. In altre parole, non esiste nessun esponente, a cui elevare 10, che possa dare un numero negativo. Ne consegue che l’operazione di logaritmo in base 10 può essere effettuata solo e soltanto su numeri positivi. Lo stesso risultato si ottiene, ovviamente, per qualsiasi base positiva.
La funzione y = log x esiste solo nell’intervallo delle ascisse che va da 0 a + ∞. In particolare, essa vale - ∞ per x che tende a zero e vale + ∞ per x che tende a + ∞.
Potremmo anche aggiungere una finezza... Vi ricordate il limite destro e sinistro? Ebbene, nel caso del logaritmo sarebbe più giusto definire il suo limite per x che tende a zero, come limite per x che tende a zero più, ossia da destra. Non può esistere il limite per x che tende a zero meno, ossia da sinistra, in quanto x non può arrivare da sinistra, dove esistono solo i numeri negativi.
Più di tante parole, vale la pena disegnare nel sistema di assi cartesiani della Fig. 36 la funzione y = log x.
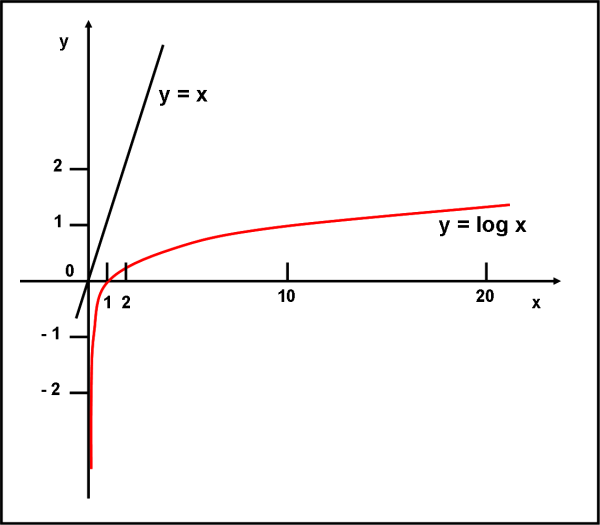
Come vedete, essa parte da - ∞ (x -->0). Poi raggiunge lo zero quando x diventa 1. Per x = 10 la funzione vale 1, per x = 100 la funzione vale 2 e via dicendo fino a + ∞. Come vedete, mentre è molto ripida all’inizio (la y va molto più veloce verso meno infinito di quanto non faccia la x andando verso 0); dopo aver tagliato l’asse delle ascisse in P(1,0) la y cresce, invece, molto lentamente, ossia tende a infinito molto più lentamente di quanto non faccia la x.
Notate che nella figura ho dovuto usare scale diverse per le coordinate x e y, dato che il logaritmo cresce molto lentamente. Facciamone un confronto con la retta y = x. Come vedete quest’ultima è ben più ripida. Potremmo dire che y = x va a infinito molto più velocemente di y = log x. Senza essere un polinomio (come abbiamo già visto) log x può essere paragonato a un polinomio sulla base della sua capacità di andare all’infinito, ossia dell’ordine del suo infinito (simile al grado di un polinomio).
Se facessimo il rapporto x/log x quanto varrebbe il suo limite per x che tende a infinito? Rispondete voi… è facilissimo!
Eppure serve a qualcosa
A cosa serve una funzione del genere? A parte i risvolti pratici che ha avuto prima dell’avvento della calcolatrice elettronica, essendo perfetta per sveltire i calcoli, basti pensare a come l’occhio riceve e trasferisce al cervello la luce che arriva da una stella. Aumentando di 100 volte la luminosità, l’occhio la “vede” aumentare solo del doppio. Aumentandola di 1000 volte, l’occhio la riceve tre volte più brillante. Abbiamo già parlato della formula di Pogson nel libro “Il Gioco delle Stelle”). In poche parole, l’occhio trasmette la luce al cervello attraverso una funzione logaritmica.
Le applicazioni sono moltissime e le leggi della fisica sfruttano molto spesso le funzioni logaritmiche.
Vi è, però, un’altra comodissima applicazione “grafica”. Si usano i logaritmi quando si vogliono disegnare, su un foglio di carta, dei valori numerici che coprono un intervallo enorme e che quindi darebbero problemi nel trovare una scala unica per tutti i punti.
Consideriamo, come esempio, un grafico in cui si voglia rappresentare una certa caratteristica y dei pianeti in funzione della loro distanza x dal Sole. Sia y la temperatura, o il diametro, o quello che volete, poco importa. Il problema è fare stare tutti i pianeti sull’asse delle x.
Cosa usare come scala? L’Unità Astronomica? Ottima scelta, ma avremmo ben tre pianeti tra 0 e 1, mentre dovremmo arrivare fino a 30 per rappresentare Nettuno. Una scala decisamente “antipatica”, dato che vi sarebbe un netto squilibrio tra quelli vicini e quelli lontani. E se, invece, usassimo come ascissa il logaritmo della distanza x? Provate… troverete che tutti i pianeti stanno entro un intervallo che va da –0.4 a 1.5. La scala è decisamente più comoda e descrittiva. La stessa cosa si potrebbe fare per le masse stellari, e molte altre cose. Ciò che per la x vale 10, 100, 1000, un milione, un miliardo, diventerebbe 1, 2, 3, 6, 9. Vi sfido a inserire in un solo foglio una grandezza che varia da 10 a dieci miliardi. Ben più facile sarebbe avere valori compresi tra 1 e 10!
Oltretutto, se il legame tra la caratteristica y e la caratteristica x fosse proprio di tipo logaritmico (cosa che capita spesso tra parametri fisici), inserendo il log x al posto della x, otterremmo una relazione rettilinea (andate a vedere le figure dell'articolo su Giove...).
Ormai sappiamo quasi tutto sulla funzione logaritmo. L’abbia studiata e abbiamo trovato anche i suoi limiti negli estremi del suo campo di esistenza (x compresa tra 0 e + ∞). Quando la ritroveremo sapremo immediatamente come trattarla anche se “mischiata” ad altre funzioni.
Operiamo con i logaritmi...
Prima di lasciarla, però, impariamo a fare alcune operazioni con i logaritmi. Poverini, sono numeri anche loro…
Proviamo a ricavare i risultati senza impararli a memoria (dopo si potrà anche fare…).
Fare il logaritmo di una somma o di una differenza è un “non-problema”… ossia bisogna lasciare le cose come sono. In altre parole, dobbiamo prima sommare i due numeri (o sottrarli) e poi fare il logaritmo della somma… Più interessante è, invece il logaritmo di un prodotto.
Si abbia:
m = log a …. (5)
e
n = log b ….(6)
Questo vuole anche dire (per la stessa definizione di logaritmo):
10m = a
10n = b
moltiplicando fra loro le due relazioni otteniamo
ab = 10n ∙ 10m
ma, per la regola delle potenze:
ab = 10(n+m)
per la stessa definizione di logaritmo si ha, però (il logaritmo è l’esponente a cui si deve elevare 10 per ottenere ab, ossia proprio (m+n)):
log ab = m + n
ma sappiamo da (5) e da (6) che
m = log a
n = log b
e quindi, sostituendo:
log ab = log a + log b …. (7)
A parole: il logaritmo di un prodotto è uguale alla somma dei logaritmi dei singoli fattori. Questa proprietà è molto utile nello studio di funzioni perché permette di eseguire semplificazioni molto importanti.
In modo analogo si determina che il logaritmo di un rapporto è uguale alla differenza tra i logaritmi del numeratore e denominatore. Basta ricordarsi, dalle proprietà delle potenze:
10m/10n = 10(m-n)
Lascio a voi la dimostrazione che è identica a quella di prima…
E che dire del logaritmo di una potenza? Ormai siamo abituati a questi giochini.
m = log a …. (8)
che vuol dire anche
10m = a
Elevo alla potenza n
(10m)n = an
Tuttavia, sappiamo benissimo che
(10m)n = 10mn = an
Per definizione di logaritmo, ho che:
mn = log an
ricordando la (8) e sostituendo m, troviamo:
n log a = log an…. (9)
A parole: il logaritmo di una potenza è uguale all’esponente moltiplicato per il logaritmo della base della potenza.
Questa relazione è molto utile, fidatevi!
Analogamente si può trovare quanto vale il logaritmo di una radice (ennesima…). Non è altro che l’inverso dell’indice della radice per il logaritmo di ciò che c’è sotto radice (il radicando). Ossia:
log a(1/n) = (1/n) log a …. (10)
Beh… questo risultato dovrebbe farvi ridere. Avendo scritto una radice ennesima come un potenza di esponente 1/n (altra proprietà che abbiamo già descritto), la (10) non è altro che la (9), cambiando n in 1/n.
Va bene, può bastare. Non gioite troppo, però. Torneremo a parlare di logaritmi, cambiando … la base. Useremo un numero veramente celebre: il numero e… Ogni cosa a suo tempo.
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






27 commenti
lim(x > + ∞) x/log x = + ∞
scusa la notazione poco pragmatica ma sono pigro..
tende ad infinito anche per x che tende ad 1 da destra, ma credo ne parlerai ancora tu!
esagerato!!!! mi vergogno a spiegarti queste cose...
Aggiungo solo che, per x che tende a 1, la funzione x/log(x) va a +∞ da destra, ma a
-∞ da sinistra, in quanto nell'intervallo da 0 a 1 il numeratore è sempre positivo, mentre il denominatore è sempre negativo ;)
Per un grafico completo, si può fare riferimento al solito Wolfram: http://www.wolframalpha.com/input/?i=y%3Dx%2Flog%28x%29&a=*FunClash.log-_*Log10-
Ciao,
Alex.
Alex!!!!! Non andare nelle cose difficili se no mi metti in crisi i meno esperti (e ti SCULACCIO!!). Io mi sono limitato a x che tende a infinito per richiamare il concetto (già spiegato) di un infinito di grado superiore e quindi limitandomi al fatto che x va più in fretta a infinito rispetto a log x. Una forma indeterminata che si risolve subito anche se log x non è un polinomio, ma sicuramente è più lento e quindi x vince la sfida!


Tu, invece, hai preso un punto di discontinuità... dai, cerca di avere pazienza.... se no ti interrogo sulla parte immaginaria della funzione
Ovviamente, sto scherzando... ma lasciamo prima digerire bene la funzione log x, poi ci divertiremo....
ok ok ok chiedo perdono :D ;)
va bene, per questa volta ti perdono
Ciao Enzo,
credo di aver capito abbastanza bene il concetto di logaritmo, però ho una domanda...
Se vogliamo calcolare il logaritmo in base 10 allora l'operazione risulta essere piuttosto semplice, come dici tu basta contare le cifre del numero , sottrarre 1, ed abbiamo il logaritmo (log1000=4-1=3). Però per i numeri diversi dalla base 10, siamo costretti ad usare una calcolatrice poichè il calcolo risulterebbe molto complesso?
Ah, il limite di x/log x che tende ad infinito è infinito
Ci sono arrivata più a naso che per effettivo ragionamento perchè ho provato a sostituire la x con un numero e questo è il risultato:
100/log100= 2 quindi se x tende ad infinito, il risultato deve essere per forza un numero positivo che tende all'infinito... Però sinceramente sento che sto uscendo dai binari...
Aiuto
Ciao gioyhofer,
per capire che x/log(x), per x che tende ad infinito, tende a sua volta all'infinito, prova a ragionare così:
per qualsiasi valore di x che sia superiore a 3*, risulterà sempre che x è più grande (maggiore) di log(x)... come dire che x aumenta più velocemente di log(x); in sostanza, più è grande x e più sarà grande il divario tra numeratore e denominatore.
Per x=5 abbiamo x/log(x)=5/log(5)=5/0.699=7.153
Per x=10 abbiamo x/log(x)=10/log(10)=10/1=10
Per x=100 abbiamo x/log(x)=100/log(100)=100/2=50
Per x=1000 abbiamo x/log(x)=1000/log(1000)=1000/3=333.333
Per x=1000000 abbiamo x/log(x)=1000000/log(1000000)=1000000/6=166666.666
Risulta quindi abbastanza intuitivo che per un valore GRANDISSIMO del numeratore x, il denominatore log(x) non conterà praticamente niente
* ho scritto "3" e non l'esponenziale "e" (equivalente a circa 2.71828182846) perché non voglio voglio fare come prima e anticipare i lavori di Enzo su argomenti come "derivate" o "logaritmi naturali" che potrebbero solo aggiungere maggiore confusione.

spero di esserti stato d'aiuto
Ciao,
Alex.
Ciao Alex,
grazie per la tua spiegazione mi risulta più chiaro ora ;) ...
Però non capisco perchè quando faccio il calcolo con la calcolatrice 100/log100 mi dà come risultato 2 anzichè 50.
Ragionandoci infatti la soluzione non è complicata 100/2=50
Forse sbaglio qualcosa io???
Grazie
Giorgia
Ciao Giorgia, se ti riferisci alla calcolatrice di Windows (o simili), per calcolare log(100) devi prima digitare "100" e poi digitare "log".
Per 100/log(100) l'ordine di digitazione deve essere questo:
"(" "100" "/" "100" "log" ")" "="
Un caro saluto,
Alex.
Ok Alex,
grazie mille,
penso che rispolvererò la vecchia calcolatrice delle superiori...
Intanto verifica se ora funziona con la calcolatrice che ti ha dato come risultato 2 anziché 50 ;)
Ciao,
Alex.
Ciao Alex,
ho trovato la mia vecchia calcolatrice e funziona bene, infatti il risultato ora è corretto... mi da 50.
A presto
Giorgia
Fantastico
Ciao Vincenzo, ho scoperto questa miniera da appena una ventina di giorni e sto spazzolando il sito in lungo e in largo. Riguardo questo Corso di matematica, che ho cominciato a leggere senza molta speranza, devo dirti che sono entusiasta le pagine scorrono che è un piacere, forse troppo velocemente. Non è il primo che affronto e ho sempre abbandonato dopo pochi capitoli, qui per ora è tutto chiarissimo e la cosa strana è che mentre leggo riemerge quel che ho studiato a scuola molto molto tempo fa cosa che non è successa con altri testi. Spero andando avanti continui questo riemergere, compatibilmente con i miei studi che si sono interrotti al primo anno di ingegneria. Non so se riuscirò a portarlo a termine ma rispetto alle precedenti delusioni sarà sicuramente una bella esperienza. Hai un dono particolare nello spiegare e coinvolgere, grazie. Nella scuola non sono molti gli insegnanti che hanno queste capacità, in ogni caso ritengo la scuola italiana ottima e il problema principale è che se i ragazzi( me incluso a suo tempo) capissero quanto è importante apprendere e sfruttare quel tempo che hanno la fortuna di avere a disposizione i professori come Te sarebbero la ciliegina sulla torta. Beata gioventù. Proseguo nella lettura, coniche sto arrivando.
Grazie e saluti.
Frank
Grazie al tuo commento, Frank, ho avuto l'opportunità di riguardare questo articolo e vi ho inserito il link ad un articolo molto interessante relativo a quanto la natura ami la spirale logaritmica... se ti interessa è questo.
Continua a leggere con fiducia, vedrai che neanche gli integrali riusciranno a scoraggiarti!
grazie Frank, di vero cuore! Parole come le tue sono il motore che continua a spingermi in quest'opera divulgativa che cerco di eseguire al massimo delle mie possibilità. E vedrai che potrai benissimo affrontare il resto della matematica, così come le grandi avventure della Scienza che purtroppo nelle scuole si ha paura (o scarsa competenza) di insegnare: RR, RG e MQ!!! Sperando, prima o poi, di catturare qualche giovane in più... Come dici bene anche tu tra le righe: l'ignoranza è una brutta bestia, la belva più terribile che ci sia. Ma, se viene affrontata con volontà di sapere, diventa mansueta come un coniglietto...
Benvenuto nel nostro circolo

e un grazie, ovviamente, anche alla diabolica Daniela che sa districarsi in una rete intricatissima di link come se fossero ... spaghetti!
Grazie Vincenzo, spero di non farmi "bannare" per eccesso di domande. Ne ho tantissime ma aspetto, prima di infierire, non voglio che ripeti cose già dette e fino a quando non ho ben spazzolato il sito le tengo in stand by.
Giusto una che riguarda questo articolo: perché nella figura 36 la retta non è a 45°?? Cosa mi è sfuggito??
Ho messo le coniche in pausa e sono passato al link segnalato da Daniela, che ringrazio. L'ho letto tre volte e ho dovuto rileggere anche questo articolo don't warry, prima di far domande voglio meditarci sopra.
Saluti
caro Frank,
nessun problema per le domande...
la retta y=x non è a 45° dato che sono diverse le scale della x e della y ...

Scusa Vincenzo, ho letto troppo faccio una pausa, se comincio a non vedere la scala "grossa" figuriamoci il resto. Domani niente lettura solo attività fisica.
Thanks
Cool
attività fisica o attività di fisica? Guarda che la RR e la MQ ti aspettano...
Bravo Vincenzo, in effetti entrambe. Non ricordo chi ha scritto un libro intitolato "La Fisica Del Golf" ma il titolo centra in pieno il gioco.
Non vedo l'ora di cimentarmi con tutte e due ma solo dopo aver finito il corso di Math. Concettualmente le ho affrontate fin troppe volte e spero "afferrate". Quel che vorrei apprendere da Te è la trattazione matematica e relativa conferma di quel che credo di sapere. Don't panic so che dovrò comunque fare atto di fiducia su molti passaggi.
Vado o mi squalificano, l'etichetta nel golf è piuttosto "Fastidiosa".
Cool
caro Frank,
se fai un tiro molto veloce, ricordati di tener conto della relatività ristretta...
Alla fine dell'articolo prometti che parlerai dei logaritmi neperiani, ma nelle lezioni successive del tuo ottimo corso di matematica non li trovo. Help!
capita di dimenticare qualcosa... Albertone. Rimedieremo