Gli infiniti di Cantor. Parte ottava: L'insieme delle parti e il teorema di Cantor.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Nell'articolo precedente abbiamo visto che anche Q è numerabile. Questa è una conseguenza del fatto che N x N e quindi anche Z x Z sono numerabili. Ci proponiamo adesso di trovare un insieme non numerabile.
L'insieme delle parti.
Dato un qualsiasi insieme X, consideriamo tutti i suoi sottoinsiemi.
L'insieme delle parti non è altro che l'insieme formato da tutti i sottoinsiemi di X, e si indica con P(X).
Cominciamo con un esempio; sia X={a,b,c}. Elenchiamo i sottoinsiemi di X.
C'è l'insieme {} (insieme vuoto) , poi i sottoinsiemi con un elemento {a},{b},{c}, quelli con due elementi {a,b}, {a,c},{b,c}, e tutto l'insieme {a,b,c}.

In tutto abbiamo otto sottoinsiemi. In generale, se abbiamo un insieme con un numero finito di elementi n quanti saranno i suoi sottoinsiemi?
Osserviamo che possiamo elencare i sottoinsiemi in questo modo (caso in cui n=3), usando una combinazione di tre elementi xyz dove x,y,z valgono 0 o 1; facciamo corrispondere al sottoinsieme una sequenza di 0,1 che ci dicono se l'elemento è presente o no. Ad esempio
101
| 1 | 0 | 1 |
| a | b | c |
corrisponde al sottoinsieme {a,c}. Così otteniamo tutti i sottoinsiemi di X.In pratica abbiamo creato una corrispondenza biunivoca fra le sequenze di 0,1 di lunghezza 3 e i sottoinsiemi di X. Quante sono le sequenze possibili? Il primo elemento lo posso scegliere in 2 modi diversi, e così pure il secondo e il terzo.
Quindi sono . Nel caso generale sono uguali a due moltiplicato n volte per se stesso, quindi
.
Per chi non fosse convinto, possiamo fare una dimostrazione formale usando il principio di induzione.
Base dell'induzione: n=1, allora ho un solo elemento a e due sottoinsiemi: {} (vuoto), {a}
Supponiamo ora che (un insieme con n elementi) abbia
sottoinsiemi; per passare ad un insieme di n+1 elementi dobbiamo aggiungere un certo elemento z, che non appartiene a
. Sia quindi
.Dividiamo i sottoinsiemi di questo insieme in due tipi; quelli che non contengono z quelli che lo contengono.

Il primo tipo è costituito da tutti i sottoinsiemi di , che sono
;il secondo si ottiene aggiungendo z a ciascuno dei sottoinsiemi di
. Sono ancora
sottoinsiemi. in tutto sono
.
Un concetto difficile.
Quando si parla di insieme delle parti abbiamo a che fare con degli elementi di un insieme che sono in realtà degli insiemi essi stessi. Questo comporta uno sforzo di astrazione notevole; dobbiamo pensare agli elementi di P(x) proprio come degli elementi ,però non dimenticandoci che sono essi stessi degli insiemi.
Riporto ora la definizione di confronto fra i numeri cardinali, anche se è già stata vista in un articolo precedente.
Confrontare la cardinalità di due insiemi.
Fino ad ora siamo riusciti a dire che due insiemi (infiniti) hanno la stessa cardinalità se esiste un corrispondenza biunivoca fra di essi. Ma se ciò non si verifica? Vogliamo cioè definire quando la cardinalità di un insieme X sia minore di quella di un insieme Y. Diremo che |X|<=|Y| se esiste una funzione iniettiva f di X in Y: f: X--->Y (e sottolineiamo che una funzione iniettiva di X in Y è una corrispondenza biunivoca di X in un sottoinsieme di Y, che non è altro che l'immagine di X, f(X)). Diremo invece che |X|<|Y| se esiste una applicazione iniettiva f di X in Y, ma tale applicazione non è suriettiva. In parole povere non copre tutti gli elementi di Y.
La cardinalità dell'insieme delle parti .
Abbiamo visto quanti sono gli elementi di P(X) nel caso X sia un insieme di n elementi: . Ma quando X è infinito?
Può esistere un f biunivoca fra X e l'insieme dei sottoinsiemi di X? Nel caso che X sia finito no di certo, perchè X ha n elementi, mentre P(X) ne ha . Sappiamo però che le stranezze avvengono nel caso degli insiemi infiniti.
X non può essere messo in corrispondenza biunivoca con P(X).
Esiste sempre una funzione iniettiva f: X-->P(X); è quella che ad x associa {x}.
quindi |X|<=|P(X)|.Dobbiamo dimostrare che f non può essere suriettiva.
Per dimostrare questa affermazione bastano poche righe (come vedremo) ma uno sforzo di astrazione notevole. La difficoltà di questa dimostrazione sta nel considerare alternativamente un oggetto sia come insieme che come elemento.
Definiamo un insieme F come il sottoinsieme di X costituito dagli x che non appartengono a f(x). Facciamo un esempio:
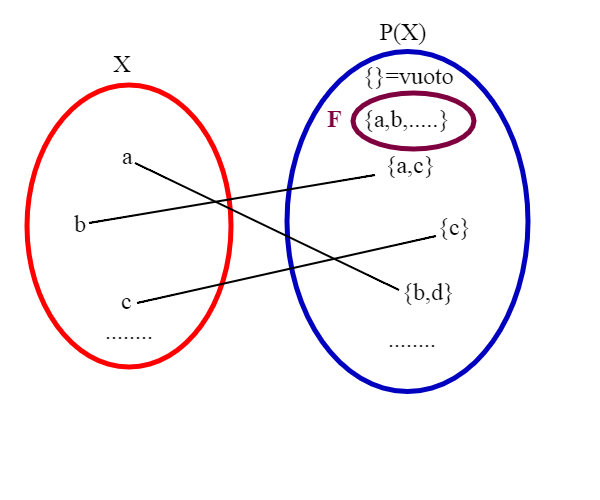
F={a,b,....} infatti a non appartiene ad f(a)={b,d} e nemmeno b, in quanto f(b)={a,c}. Invece c non appartiene ad F, in quanto c appartiene all'immagine f(c)={c}. Questo è solo un esempio di come è definito F .Dobbiamo ora ragionare più in generale.
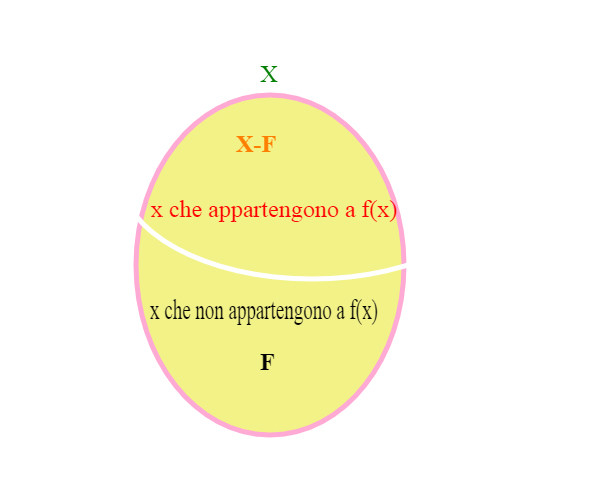
Abbiamo detto che F={x appartenenti a X tali che x non appartiene a f(x)}. Questo F è un certo sottoinsieme di X. Questa definizione divide l'insieme X in due parti complementari:
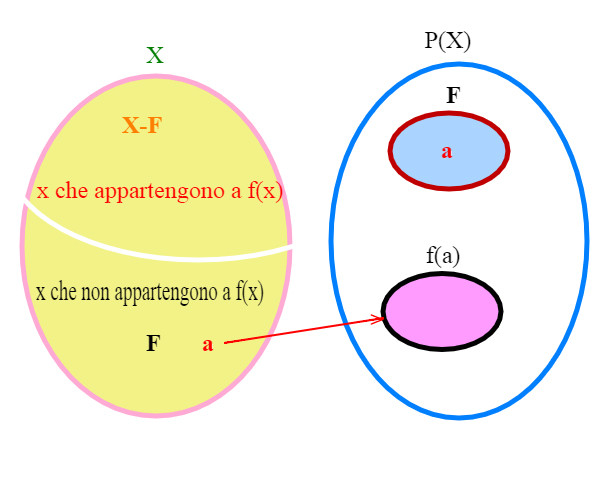
Comunque si scelga a appartenente a X, il sottoinsieme F di X non è uguale a f(a). Infatti, se a appartiene a F, allora a non appartiene a f(a) per la definizione di F. Ma F e F(a) sono due insiemi; se non hanno in comune a allora sono diversi.
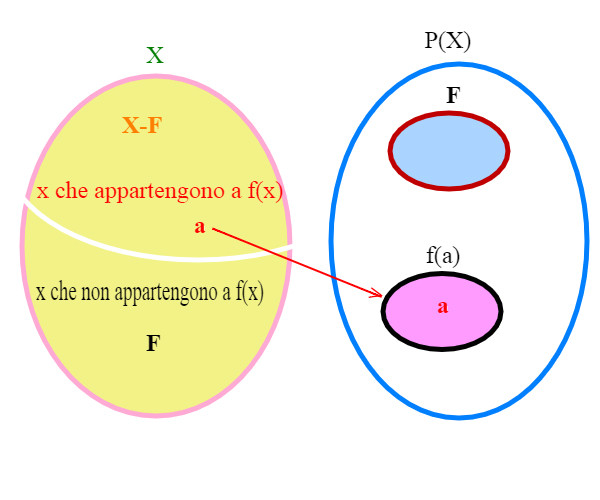
Allo stesso modo, se a non appartiene a F, allora a appartiene a f(a).
Quindi in entrambi i casi a appartiene solo ad uno dei due insiemi F ed f(a), ma non all' altro. Ma F e f(a) sono due insiemi; se non hanno in comune a allora F e f(a) sono diversi (due insiemi sono uguali solo se contengono tutti gli stessi elementi).
Abbiamo dimostrato che F è diverso da f(a) per ogni a appartenente a X, e quindi che F non appartiene all’ immagine di f. In altre parole, f non è suriettiva.
Quindi, per come abbiamo definito il confronto fra la cardinalità di due insiemi,
|X|<|P(X)|
Teorema di Cantor: non esiste un insieme di cardinalità maggiore di ogni altro insieme.
La cardinalità dell'insieme delle parti di P(X) è maggiore di X. P(X) è esso stesso un insieme, chiamiamolo A=P(X). |P(A)|>|A|. Possiamo ripetere questo procedimento all'infinito. Non esiste un numero cardinale più grande di tutti.
Nel caso che X sia N, l'insieme dei naturali, per analogia con il caso finito, |P(N)| si indica con , quindi
. Quindi in particolare abbiamo trovato un insieme confrontabile con N che non è numerabile.
Articoli precedenti:
Cantor, parte settima La numerabilità di Q
Cantor, parte sesta:Il minimo ordine di infinito
Cantor pare quinta,Il principio di induzione
Cantor, parte quarta. L'abergo di Cantor
CANTOR parte Terza, gli insiemi numerabili
CANTOR parte Seconda: Corrispondenze e funzioni
CANTOR parte prima, gli insiemi
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica





