Nelle due puntate precedenti abbiamo visto la forma che può prendere la lagrangiana di un corpo libero (qui) e di un corpo vincolato ad una traiettoria (qui).

Esiste una equazione, l'equazione di Eulero-Lagrange, che ci dice come elaborare la lagrangiana per ottenere l'equazione del moto. Questa elaborazione richiede di fare alcune derivate della lagrangiana.

Qui ho proposto un piccolo percorso per familiarizzare con la forma di alcune di queste derivate  che appaiono nella equazione di Eulero-Lagrange.

L'obiettivo del percorso era quello di abituarsi a vedere derivate di una stessa funzione fatte rispetto a diverse variabili. Probabilmente lo avevate già capito. Accade spesso per le grandezze fisiche come la lagrangiana che possono dipendere da più variabili come posizione, tempo, velocità. Nella equazione di Eulero-Lagrange c'è tutto il campionario e oltre... 

Le soluzioni proposte nella domanda della prima tappa possono essere tutte derivate della funzione della prima colonna e solo questione rispetto a quale variabile è fatta la derivata. Ad esempio, prendo la funzione , la posso derivare rispetto a w, la posso derivare rispetto al tempo t o la posso derivare rispetto ad un'altra variabile, chiamiamola z, che non ha alcuna influenza su w:

A chi ha meno confidenza con le derivate può venire la voglia di capire meglio come si ottengono le tre derivate.

Non serve ricordare tutta la teoria delle derivate, bastano poche cose: una tabella delle derivate notevoli dove ci sono i "prototipi" delle derivate più comuni (magari teniamola a portata di mouse aprendola su una nuova scheda), ricordare come si fa la derivata di una funzione composta che trovate qui, comunque la ripeto più avanti, e poco altro. Eseguo i passaggi in modo esteso commentandoli.

1. una costante può essere portata fuori della derivata
2. ho applicato il prototipo della derivata rimasta: 

• F non dipende da z. La derivata è 0 poiché qualsiasi variazione di z non fa variare F. Qui vediamo anche che non sempre se la derivata di una funzione è nulla la funzione è una costante, potrebbe essere una funzione di  variabili diverse da quella di derivazione.

1. la variabile w la vedo come una funzione del tempo. Pensate alla coordinata dello slittino vista in uno degli esempi di lagrangiana. E' certamente un funzione del tempo, anzi è proprio la funzione che stiamo cercando. Quindi questa è una funzione di funzione  dove   e 
2. applico il prototipo di derivata di funzione di funzione
3. la derivata del primo termine è quella trovata sopra, la derivata del secondo la scrivo in modo più compatto

Per capire meglio il significato fisico di quest'ultima derivata per poi fare un altro passo avanti, conviene continuare a ragionare ancora su questa funzione .

Pensiamo w come la coordinata che indica la posizione di un oggetto in movimento ed F come una grandezza fisica che dipende dalla posizione. Tanto per rendere la situazione più tangibile, immaginiamo che w sia il chilometraggio lungo una strada ed F la temperatura misurata lungo questa strada.

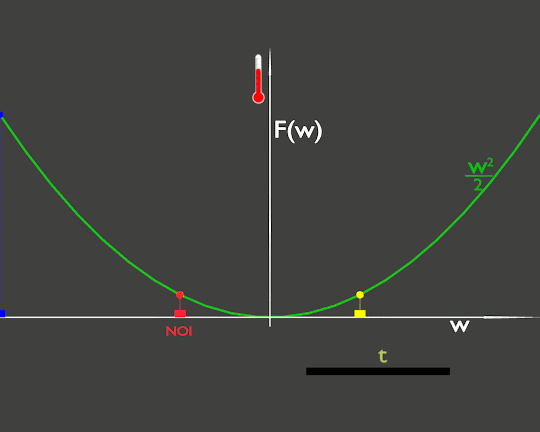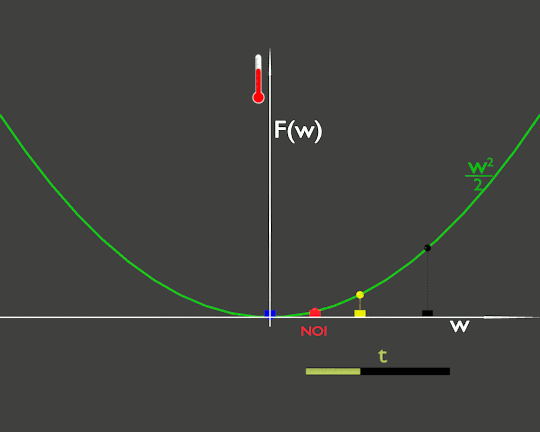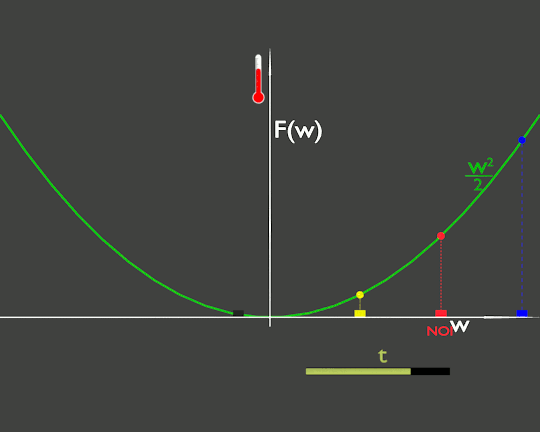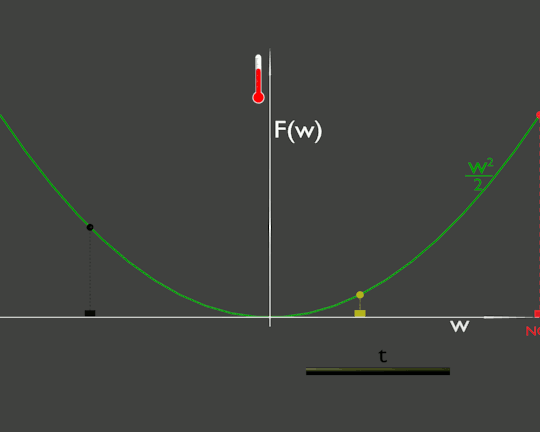
Ora percorriamo questa strada con la nostra auto che identifichiamo con il rettangolino rosso della figura. La nostra posizione, w(t), è una funzione del tempo. Osservando il termometro della nostra auto vedremmo che la temperatura varia nel tempo. Graficamente è rappresentata dall'altezza del cerchietto rosso che segue l'andamento della funzione F(w).

In realtà  la temperatura dell'ambiente non sta cambiando, il grafico (verde) della temperatura rimane sempre lo stesso, ma siamo noi che ci stiamo spostando da zone più fredde a zone più calde o viceversa.

La rapidità di variazione della temperatura dipende dalla nostra velocità, infatti nella derivata sopra appare a moltiplicatore . La variazione di temperatura vista dall'auto blu che ci sta sorpassando è più rapida della nostra e quella dell'auto nera che percorre la strada nel verso opposto è opposta alla nostra.

Vedendo il termometro che sale potremmo domandarci: è la temperatura dell'ambiente che sta salendo o sono io che mi sto spostando in una zona più calda?

La risposta si può ottenere facilmente. Mi fermo alla prima piazzola di sosta, come l'auto gialla, e continuo ad osservare il termometro. Nel caso che stiamo vedendo la temperatura rimane costante, infatti il cerchietto giallo nella animazione è fermo. Dal punto di vista matematico è dovuto al fatto che F(w) non dipende esplicitamente dal tempo, ma dipende dal tempo solo tramite w. Se la nostra w(t) è costante, cioè siamo fermi, rimane costante anche F(w).

Per avere un paragone vediamo cosa accade se fosse la temperatura dell'ambiente che cambia, per semplificare la facciamo cambiare uniformemente nello spazio. Questo è rappresentato da una funzione F(t) che dipende esplicitamente dal tempo t e non dipende esplicitamente da w. Nella figura

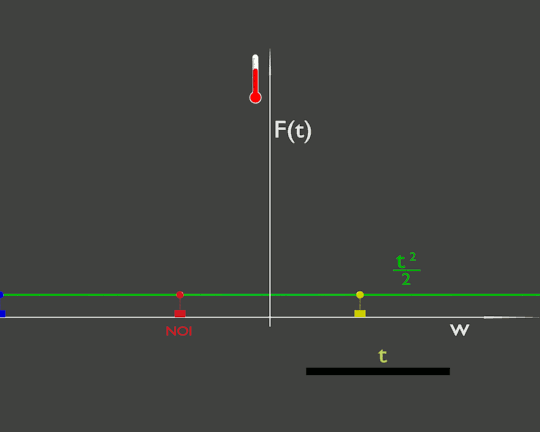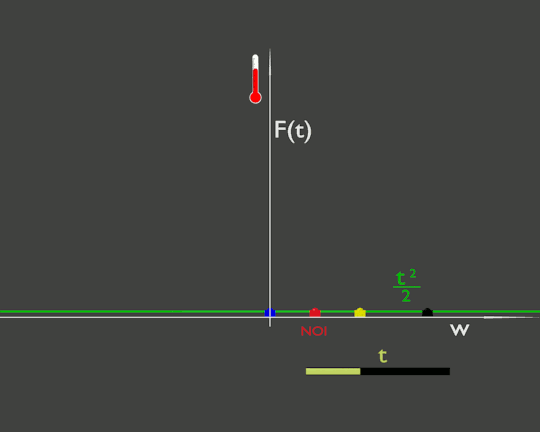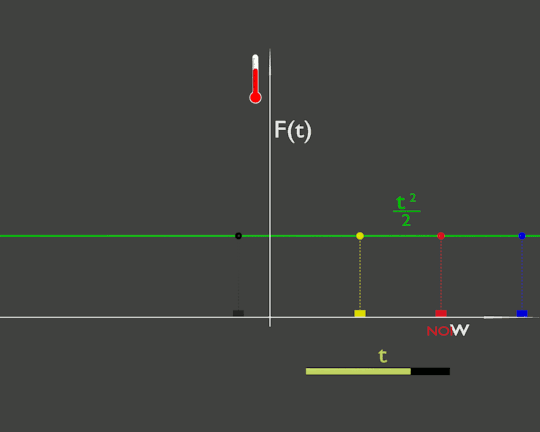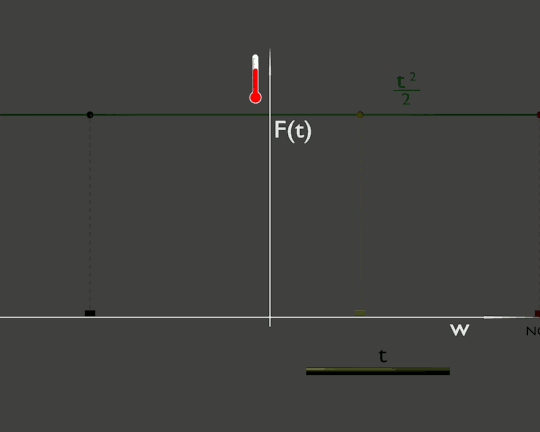
Anche qui la temperatura che misura la nostra auto (cerchietto rosso) varia, ma perché sta variando la temperatura dell'ambiente, la linea verde che si muove, e non perché ci stiamo muovendo.

In questo caso anche se ci  fermiamo, come l'auto gialla, la temperatura continuerà a cambiare.

Questa operazione di fermarsi e trovare come varia una grandezza lasciando scorrere solo il tempo in matematica si chiama derivata parziale rispetto al tempo e viene indicata con questo simbolo:  .

Quindi non meravigliatevi se vi capiterà di vedere un cartello come questo.

Qui ci siamo concentrati su tempo, ma la derivata parziale si può fare rispetto ad ogni altra variabile.

Il procedimento matematico per farla è semplice. Devo fare la derivata della funzione considerando solo la variabile scelta dove appare esplicitamente e non dove appare implicitamente in un altra variabile (come t  in  w(t)), considerando quindi tutte le altre variabili costanti. Nel nostro caso abbiamo fissato la posizione fermando la nostra auto, ma in generale tutte le altre variabili dalle quali può dipendere la funzione sono considerate costanti non solo quelle della posizione.

Quindi, nel nostro primo caso:

La derivata parziale è nulla perché t non appare esplicitamente e tutto il resto deve essere considerato costante. Nel secondo caso t appare esplicitamente quindi la derivata parziale non è nulla:

Le due derivate sono uguali poichè in questa funzione non ci sono altre variabili oltre alla variabile di derivazione t.

Per distinguerla dalla derivata parziale, l'altro tipo di derivata è chiamata derivata totale.

Con questo abbiamo fatto la conoscenza con tutti i tipi di derivata contenuti nella equazione di Eulero-Lagrange e siamo pronti per affrontarla nella prossima puntata.

Ora che li abbiamo domati, i draghi delle derivate non appaiono più così terribili. Anzi possiamo cavalcarli per farci portare dalla equazione di Eulero-Lagrange.

Aggiungo una postilla per vedere un caso più generale rispetto ai due visti sopra. Non è necessario per la prossima puntata, ma non è male vederlo.

Nei due casi visti c'era una funzione, F, e due variabili, w e t. La funzione F dipendeva esplicitamente da una sola delle due variabili, F(w) ed F(t). Tra le parentisi sono elencate le variabili dalle quali la funzione dipende esplicitamente.

C'è anche la possibilità che possa dipendere esplicitamente da tutte due le variabili, F(w,t), come ad esempio

      e    

Ora che conosciamo le derivate parziali  è possibile scrivere in una forma più generale la derivata di una funzione di funzione in modo che sia valida anche per queste funzioni di funzioni.

Se ci fossero altre variabili, per ciscuna si dovrebbe aggiungere un termine del tipo di quello per w.

Per chi volesse continuare a ragionare su queste derivate propongo alcune domande.

Quali sono le derivate parziali  e totali      delle due funzioni       e     ?

Se nella espressione della derivata totale al posto di F(w,t) ci fosse una F(t), l'espressione può essere scritta eliminando un termine. Come?

Stessa domanda con F(w) al posto di F(w,t).

La serie completa degli articoli sulla Lagrangiana la trovate QUI