Categorie: Fenomeni astronomici
Tags: aberrazione annua aberrazione della luce parallasse annua
Scritto da: Vincenzo Zappalà
Commenti:0
Aberrazione della luce. 2bis: un piccolo contributo alla chiarezza *
Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.
Questo breve articolo vuole dare un ulteriore contributo per la spiegazione della differenza tra parallasse e aberrazione, di cui abbiamo parlato QUI. Quando la trattazione sarà inserita negli approfondimenti, questa “aggiunta” sarà inserita nella posizione più consona. Purtroppo, ciò che a volte sembra ovvio per chi ne ha avuto a che fare per tanti anni, può sollevare dubbi e confusioni non previsti nei non addetti ai lavori… E’ meglio, quindi, agire subito. Qui sta la peculiarità di questo Circolo: un miglioramento continuo dato da una continua collaborazione.
Costruiamo una figura (Fig. 1) di massima semplicità, in cui sono state inserite due stelle: la prima, MV, è una stella vicina per la quale ha senso misurare la parallasse annua. La seconda, ML, è una stella lontana che quindi non forma nessun angolo parallattico. Entrambe le stelle sono nella direzione perpendicolare al piano orbitale terrestre.
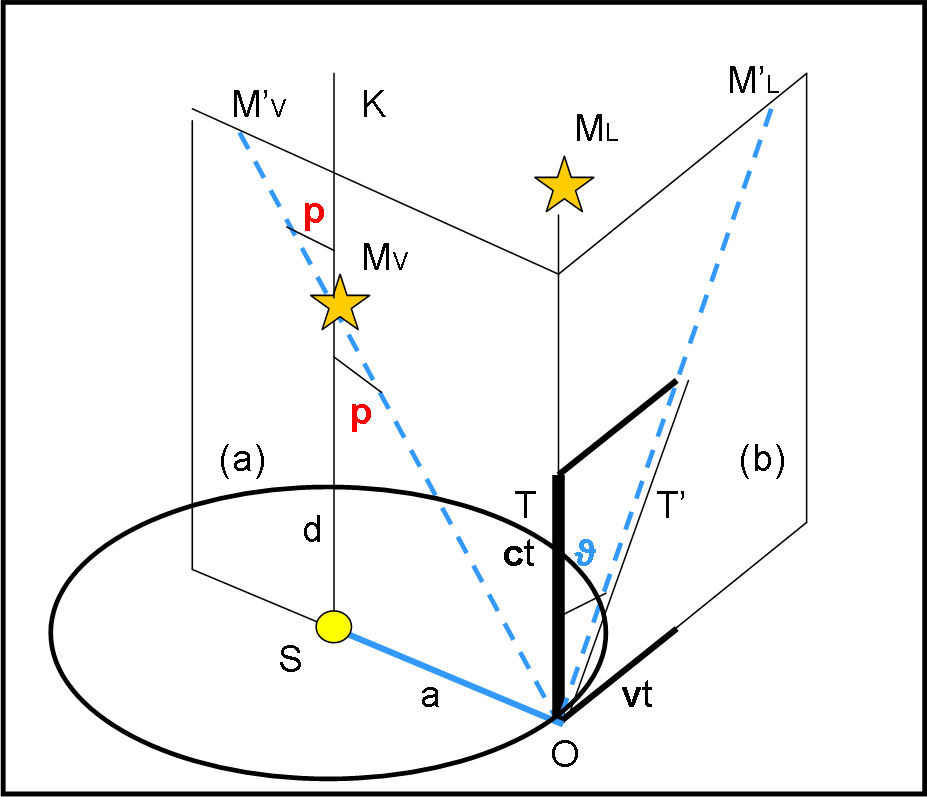
Individuiamo due piani perpendicolari tra loro. Il primo è quello che contiene la posizione O dell’osservatore, il Sole S e la stella vicina MV (piano (a)). Il secondo piano è quello che contiene la stella lontana ML e la direzione del moto della Terra (piano (b)). Nel piano (a) si misura la parallasse annua, data dall’angolo p. Nel piano (b) abbiamo il telescopio T che vorrebbe puntare la stella ML. Tuttavia, a causa del moto dell’osservatore eseguito con velocità v, il telescopio va inclinato dell’angolo ϑ, angolo di aberrazione annua. Come si vede bene i due piani sono perpendicolari e tali sono anche gli spostamenti delle stelle apparenti M’L e M’V. Il tutto è comandato dal fatto che v è perpendicolare alla direzione del Sole.
Penso che questa figura sia più che sufficiente per vedere come agiscono parallasse e aberrazione. Tuttavia, abbiamo usato due stelle separate. Possiamo però fare un passetto in più… Se è vero che per una stella lontana non si può misurare la parallasse, ma solo l’aberrazione, non è vero il viceversa. In altre parole, per una stella vicina MV si può misurare sia aberrazione che parallasse.
Se qualcuno vuole provare la propria comprensione dei due fenomeni, può andare avanti da solo e poi verificare il ragionamento. Noi proseguiamo ugualmente.
La Fig. 2 mostra questa situazione.
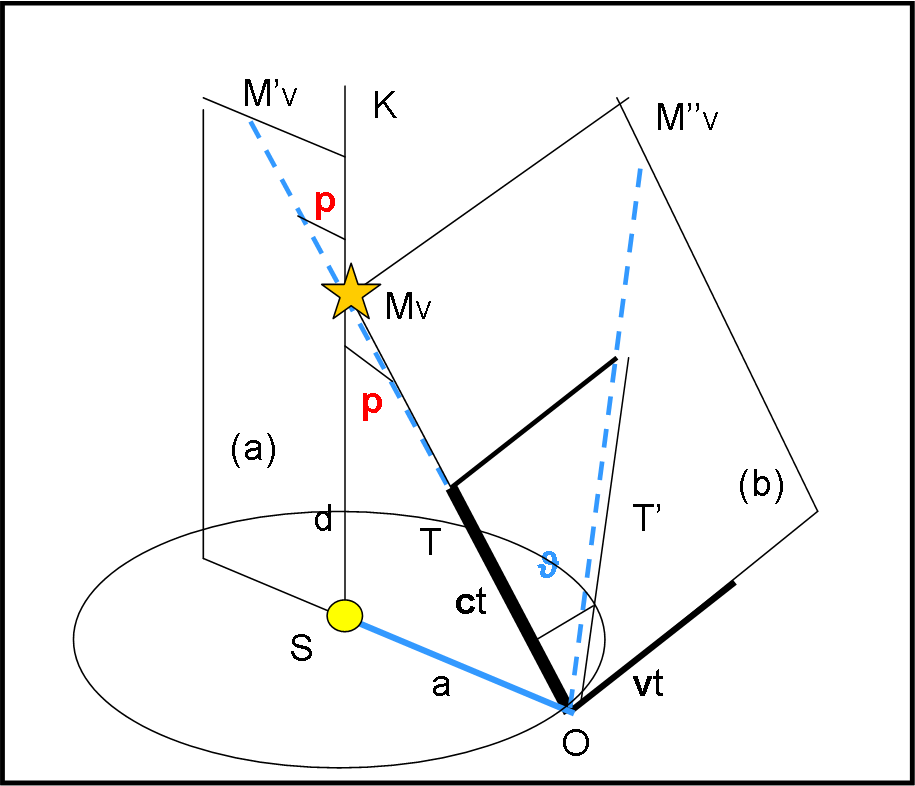
La stella è ora una sola, MV. Il piano (a) è sempre lo stesso così come la definizione di angolo di parallasse. Il piano (b) deve cambiare, dato che deve contenere sia la direzione del moto della Terra (sempre perpendicolare alla direzione del Sole S), ma anche la stella MV (che non si trova, perciò, per l’osservatore O, nella direzione perpendicolare al piano orbitale, come capitava prima per la stella ML). La direzione teorica del telescopio T dovrebbe essere quella diretta verso MV, ma, a causa del moto della Terra, essa deve piegarsi di un certo angolo ϑ, nel piano individuato dalla direzione O-MV e da quella del moto terrestre. Notiamo, comunque, che i due piani rimangono perpendicolari tra loro, così come gli spostamenti.
Spero di avere cancellato ogni dubbio… nel caso, sono sempre qui: chiedete senza paura! Nessuno è perfetto (io per primo!).





