Quiz: Il gatto e il topo.
L'esposizione del quiz sarà brevissima, e anche la soluzione lo è, pur non essendo proprio semplice. Potrebbero essere utili gli articoli che potete trovare qui, qui e qui. Del resto, per chi è già chiara la definizione di probabilità, penso che il quiz sia risolvibile in maniera completamente intuitiva.
Un topo si sposta completamente a caso fra delle scatole comunicanti con delle porticine.
Ci sono cinque scatole, che numeriamo con 1, 2, 3, 4, 5 , poste consecutivamente come in figura.
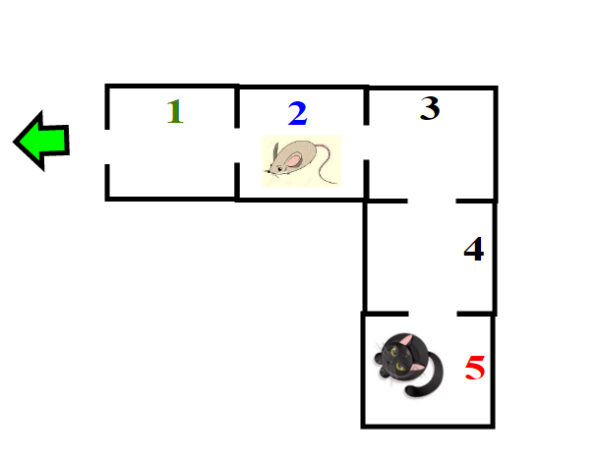
Inizialmente il topo si trova nella scatola 2. Se arriva nella scatola 1, vede l'uscita e si salva.
Ma se finisce nella scatola 5, dove sta in agguato un gatto, viene mangiato(chiaramente il gatto non riesce a passare per la porticina). Qual è la probabilità che il topo si salvi?
(La soluzione è chiaramente un numero, compreso fra 0 e 1.)
Invito tutti a partecipare, autori maghi e maghetti compresi.
Grazie.






77 commenti
Buonasera Umberto,
il mio ragionamento è questo:
il topo ha 6 possibilità di stazionamento complessivamente, 5 scatole + l'uscita:
se, in un determinato momento si trova nelle scatole 1, 2, 3, 4, o all'uscita, si salva;
se, in un determinato momento si trova nella scatola 5, non si salva;
la probabilità di salvarsi dovrebbe essere 5/6;
la probabilità di non salvarsi 1/6
grazie per la risposta Andy ..chiaramente per adesso non posso dire niente..
Dalla posizione 2 ha 50 % ossia 0,5 di 1 per l’uscita scatola 1
Se passa alla scatola 3 altro 0,25 perché torna alla 2 a caso (testa o croce) può annullare la scelta o salvarsi verso scatola 1
Se passa alla 4, lo 0,125 di entrare nella 5. …
Sono le ore 10 ma la settimana scorsa erano le ore 11!
Provo una soluzione semplificata, forse troppo, che dà al topo una probabilità del 75% di salvarsi.
Il topo nella casella 2 può imboccare subito la strada per lui giusta con probabiltà 0,5 o andare nella casella 3 con probabilità 0,5.
A questo punto applico la semplificazione sfruttando due considerazionioni:
Mi viene da dire che una volta arrivato alla casella 3 il topo ha ancora il 50% di possibilità di salvarsi e il 50% di finire il bocca al topo.
Quindi la probabilità di salvarsi per il topo sarebbe 0,5+0,5 0,5=0,75
mi sembra che siamo nella strada giusta.. sentiamo anche altre opinioni
Se io topo sono in 2, ho il 50% di probabilità di andare in 1 e salvarmi e il 50% di probabilità di andare in 3, senza però essere ancora spacciato. Supponendo di andare in 3, una volta in 3 ho il 50% di probabilità di tornare in 2, allontanandomi dal diventare pasto per il gatto, e il 50% di probabilità di proseguire in 4. Se vado in 4, avrò infine un 50% di probabilità di tornare in 3 e il 50% di finire in 5 e addio.
Quindi, con riferimento allo stato iniziale di quando ero in 2, alla fine mi pare che dovrei avere
0,5+0,5*0,5+0,5*0,5*0,5 = 0,875 = 87,5%
di probabilità di salvarmi.
Ho provato a giungere allo stesso risultato immaginandomi tutti i possibili percorsi partendo da 2, ma mi ci sono perso perché l'ipotesi di partenza era che i percorsi fossero del tutto casuali. Quindi teoricamente avrei probabilità anche di fare avanti e indietro indefinitamente tra 2 e 4 o andare da 2 a 4 poi a 3 tornare a 4 etc . Ma non era "mondo cane" ?
La casella in cui si trova inizialmente il topo è determinante per valutare la sua probabilità di salvezza.
Se il topo si trovasse nella casella 5 sarebbe certamente in bocca al gatto. la probabilità di salvezza sarebbe in tal caso 0%.
Se, invece, si trovasse nella casella 4, avrebbe il 50 percento di possibilità di finire nella 5 , dal gatto, e il 50% di andare in direzione della uscita, ma questo non significa salvezza, perché la mossa successiva potrebbe riportarlo da dove era partito, e da lì , successivamente, nella casella del gatto.
Quindi posso dire che con la prima mossa ( dalla casella iniziale 4) la probabilità di finire "subito" in bocca al gatto è il 50% ma esiste, in più, una probabilità futura di fare la tessa fine.
Questa situazione è conseguenza diretta del fatto che le scelte sono sempre casuali.
Una cosa è certa: il topo ha il raffreddore, altrimenti capirebbe, dalla intensità dell'odore del gatto, quale direzione è quella più sicura per allontanarsene. Ma in questo caso la sua scelta non sarebbe casuale.
Se, come sembra di capire, in una casella qualsiasi, le scelte di andare a sinistra o a destra, sono sempre equiprobabili, allora non sono escluse neppure configurazioni di stallo, in cui il topo entra in un loop di "avanti e indietro" senza fine, muovendosi tra due caselle adiacenti, ad esempio: la 2 e la 3 , oppure la 3 e la 4, o ancora, in un loop più ampio, una sequenza, random, di più caselle, 2, 3 , 4 e ritorno, sempre senza uscire né finire nella casella del gatto. Come andrebbe interpretata questa situazione? il topo è da considerarsi salvo perché non è mai giunto alla casella 5 ? Oppure si salva dal gatto ma, non uscendo all'aperto, resta intrappolato in una sequenza di mosse ciclica ed infinita ( e muore di fame)?
Un modo diverso di guardare al problema è invece quello di considerare che il topo, partendo da dove si trova, nella casella 2, deve eseguire per tre volte consecutive la scelta di andare verso il gatto. Quindi 0,5 ^3 = 0,125 probabilità di farsi mangiare e, corrispondentemente 1- 0,125 = 0, 875 di non farsi mangiare. Ma questo ragionamento non considera la possibilità di tornare sui propri passi ad ogni mossa.
dopo gli ultimi commenti la discussione si sta facendo sempre più interessante ..ma il gioco continua!
Se oltre a maghi e maghetti, possono partecipare anche i papalli, provo a sparare una papallata:
Secondo me la probabilità che il topo rimanga in vita è 0,5 x 0,5 = 0,25 (ma di questo calcolo non sono convinto... )
)
Se, poi, vogliamo chiedere un suggerimento a Schroedinger, non dobbiamo fare altro che mettere un coperchio alla scatola, non guardare cosa succede e... va beh... meglio lasciar perdere oppure chiedere a Mauritius (QUI) che se ne intende!
Un modo per arrivare alla probabilità che cerchiamo più formale di quello che ho inviato ieri potrebbe essere questo.
Un topo che si trovasse in una delle caselle 2, 3 o 4 avrebbe una certa probabilità di arrivare alla casella 1, cioè di salvarsi. Al momento non conosco queste probabilità, ma posso riferirmi ad esse chiamandole S2, S3 e S4. S2 è la probabilità che stiamo cercando. Estendendo il ragionamento alle caselle 1 e 5 avrei S1=1 ed S5=0, savezza certa o fine certa.
Per come è definito il comportamento del topo nel quiz, queste probabilità non dipendono da come il topo è arrivato ad una delle caselle. Questo mi permette di mettere in relazione queste probabilità limitando il ragionamento ai soli percorsi fino alle caselle adiacenti:
S2=0,5 S1+0,5 S3 = 0,5+0,5 S3
S3=0,5 S2+0,5 S4
S4=0,5 S3+ 0,5 S5=0,5 S3
Posso considerare S2, S3 ed S4 come incognite legate tra loro da queste tre relazioni. Sostituendo nella seconda relazione S2 ed S4 con le loro espressioni nella prima e terza relazione ottengo:
S3=0,5 (0,5+0,5 S3+0,5 S3)=0,25+0,5 S3
0,5 S3=0,25
S3=0,25/0,5=0,5
S2=0,5+0,5*S3=0,5+0,25=0,75
S4=0,5 S3=0,5 0,5=0,25
Quindi la probabilità che stiamo cercando è 0,75.
In verità, Schroedinger analizzava le probabilità di sopravvivenza del gatto, che nel caso del quiz non sono messe in discussione. Dovrei approfondire la ricerca per vedere se c'è anche un "topo di Shroedinger" che possa darci qualche idea...
vedo dei ragionamenti validi, . portano a due risultati diversi ; perché ?
altra domanda: É possibile rappresentare il problema con una specie di albero che rappresenti il susseguirsi degli eventi con le rispettive probabilità? Ciò semplificherebbe il problema.
piccolo commento:
sicuramente la probabilità di finire in bocca al gatto deve essere maggiore di 0.125. 0.125 è la probabilità che il topo passi direttamente da 2 a 3 a 4 e a 5. Abbiamo ancora da spartire una probabilità di 0.5 - 0.125 = 0.375 ...
I vari loop dovrebbero al limite portare a 0 ...
o sbaglio?
Mi fermo qui...
su una cosa hai perfettamente ragione, e sono molto contento che sia stato messo in luce..i loop hanno probabilità nulla!
Stavolta mi immedesimo nel gatto e mi chiedo quale è la probabilità che ho di mangiarmi il topo che inizialmente è in 2. Perché io lo possa mangiare, il topo deve andare a finire da me nella scatola 5. Per prima cosa , la prima scelta che il topo dovrà fare in 2 è quella di passare in 3. Questa scelta ha il 50% di probabilità di essere presa. Se viene presa, il topo passa in 3. A quel punto, perché io me lo possa mangiare, il topo non dovrà tornare indietro ma proseguire in 4. Anche qui, la probabilità che il topo scelga di proseguire in 4 è del 50%, ma devo tenere conto che dalla 2 aveva scelto di passare alla 3. Quindi la probabilità che dalla 3 passi alla 4 è il 50% del 50%, cioè 0,5x0,5. Infine, per poter finalmente papparmelo, dalla 4 dovrà passare nella 5. Anche in questo caso, poiché potrebbe anche tornare indietro nella 3, la sua scelta di proseguire nella 5 ha il 50% di probabilità di essere presa. Anche qui , il 50% del 50% del 50%, cioè 0,5x0,5x0,5 = 0,125. Quindi, la probabilità di mangiarmi il topo è del 12,5 %. Risultato che rispecchia quello trovato prima come topo, cioè l'87,5% di probabilità di salvezza.
Ora che ci penso, sempre come gatto, ma le scatole sono coperte ? Potrei evitare tanti calcoli e arrivare subito al dunque
Pensandoci meglio, credo che la differenza tra i due risultati diversi per la probabilità del topo di salvarsi (87,5 % e 75%) sia dovuta al fatto che nel caso più ottimistico si considera salvezza anche il trovarsi in 3 o 4 , senza necessariamente arrivare in 1. E' chiaro, infatti, che se per salvarsi il topo deve arrivare nella 1, e non semplicemente girovagare nelle altre purché non nella 5, le probabilità che ha di farlo scendono. Quindi credo che il risultato corretto sia il 75%.
Insomma, il topo ha una probabilità di salvarsi che può essere: dal calcolo più pessimistico, a quello più ottimistico, 0,25 , oppure 0,75, oppure 0,8333, oppure 0,875. Vista l'incertezza lascerei decidere al topo cosa preferisce.
Comunque, riprendendo una nota a margine di Scherzy, c'è una novità...
Tra le carte inedite di Schroedinger, pare sia stato rinvenuto un rapporto di ricerca sulla variabilità statistica dei risultati di un esperimento, in funzione delle convinzioni a priori dei soggetti che partecipano all'esperimento stesso.
Il lavoro, intolato "die glückliche Maus" ( il topo fortunato) avrebbe dovuto apparire sulla famosa rivista tedesca "Zeitschrift für Wahrscheinlichkeit und Statistik", ma non è stato mai pubblicato per motivi che non sono tuttora chiari.
L'esperimento descritto è molto simile a quello proposto nel quiz, salvo una modifica alla ipotesi di indifferenza nelle scelte, apportata da Schroedinger, dopo vari test condotti sul campo.
I topi di Schroedinger erano stati divisi in due gruppi: il primo costituito da topi che si ritenevano fortunati, il secondo da topi che , viceversa, ritenevano di essere sfortunati.
Quando un topo "fortunato" entrava nella tana del gatto, lo trovava addormentato e aveva il tempo di tornare alla casella precedente, salvandosi. Viceversa per i topi "sfortunati" il gatto era sempre pronto.
Si veniva così a creare una distribuzione bipolare dei risultati che perturbava drammaticamente i valori di probabilità calcolati con i metodi classici, che non tenevano conto delle convinzioni dell'osservatore-attore e dei relativi riflessi sull'esito finale.
Esiste anche un lungo carteggio tra Schroedinger e Heisemberg su questo argomento. Per un certo periodo Heisemberg aveva anche pensato di enunciare una sorta di "principio di autodeterminazione", proprio basato sul paradigma del topo fortunato.
Lasciando da parte teorie ed esperimenti, ad un osservatore attento non sfugge il fatto che, a parità di condizioni, la probabilità di ottenere un risultato positivo non è la stessa per tutti, il calcolo matematico fornisce solo una idea "media" delle chances, gli eventi "casuali" sono programmati, in realtà, dal destino individuale. Insomma, che chi ha c... e chi non ce l'ha.
Il mio ragionamento è il seguente:
il 50% si salva subito. Del restante 50%, ne viene mangiate dal gatto il 12,5 sicuramente (o.5 x 0.5 x 0.5).
Chi sono i restanti topi? Ad esempio, quelli che sono arrivati sulla quarta casella e che sono tornati indietro. Anche loro sono il 12.5 (nell'ultima scelta si sono ritirati). Ora, però sono di fronte alla possibilità di andare in 2 o di tornare in 4. il 6% torna in 4. A questo punto il 3% finisce nuovamente in bocca al gatto. E via dicendo...
alla fine bisogna però trovare un numero solo..
Non so quale sia la ragione della differenza tra i due risultati (87,5% e 75%).
Non può essere però quella di considerare come risultati positivi il permanere del topo in loop tra le caselle intermedie (2, 3 e 4). Poichè non ci siamo dati limiti di tempo, la probabilità finale di trovare il topo in questi loop è nulla.
Ho l'impressione che i ragionamenti che seguono i possibili percorsi del topo richiedano un numero infinito di passi. Se terminate ad un numero finito danno un risultato approssimato, anche se sempre migliore con il crescere della lunghezza dei percorsi considerati.
Forse una possibilità potrebbe essere quella di trovare una espressione ricorrente che possa essere calcolata come limite all'infinito dei passi. Io non l'ho trovata. Per questo ho cercato un approccio diverso che considera subito i valori finali delle probabilità e li mette in relazione tra loro.
Quello che avete fatto è più che sufficiente; i loop infiniti hanno probabilità nulla. In ogni caso è la probabilità teorica quella che ci interessa,discendente dalla sua definizione, non l'evoluzione del processo nel tempo, ovvero le cosiddette "passeggiate aleatorie". Adesso riesco a capire anche cosa intendeva Vincenzo, applicare proprio una relazione ricorrente e sommare poi i valori di una serie. Ma non era mia intenzione spingermi a tanto. Resto dell'opinione che per chiarire bene la differenza fra 87,5% e 75% sarebbe opportuno studiare le alternative del topo per salvarsi tramite un grafico, ovvero quello che in matematica si chiama grafo. Lì secondo me si vede meglio il tutto.
Una domanda ai meno pigri....
Se mettiamo inizialmente il topo nella posizione 3, invece che nella 2 possiamo dire che le sue probabilità di sopravvivenza sono del 50% ?
Mentre se lo mettiamo inizialmente nella posizione 4 sono del 25 ?
E, per finire, in accordo con il ragionamento più che condivisibile di Fabrizio, partendo dalla posizione 2 il topo ha il 75% di speranza?
La distanza tra la salvezza e la perdizione sarebbe in un certo modo graduata dal numero di celle interposte, con una distribuzione speculare sui due lati e il perfetto equilibrio nella stanza centrale, baricentrica, (sto naturalmente parlo di un numero di celle intermedie dispari.
Rispondo a questo commento di Maurizio
Caro Mau,
al di là dell'esperimento che ti sei inventato (nel dubbio ho fatto una ricerca con Google, non si sa mai, specialmente quando c'è di mezzo un "tipaccio" come Schroedinger... complimenti per la fantasia!), le tue considerazioni sulla statistica e su quanto gli esiti di una determinata situazione siano influenzati dall'atteggiamento mentale con la quale la si affronta, sono ampiamente condivisibili. Sono convinta che anche il concetto di c*** o non-c*** dovrebbe essere rivisto alla luce di tali considerazioni.
Non a caso, studi per ora solo statistici, sembrano dimostrare una relazione tra l'ottimismo del malato e la sua probabilità di guarigione anche in caso di malattie gravi (basta scrivere "guarigione e ottimismo" su un motore di ricerca per farsi un'idea).
Quindi ben venga la statistica e il calcolo delle probabilità, ma, nella vita vera, lasciamo perdere questi calcoli e cerchiamo di cotruirci il c*** da soli!
P.S.
Bel quiz, Umberto, complimenti!
A proposito di statistica... http://www.infinitoteatrodelcosmo.it/2017/04/20/racconti-mauritius-lesempio-viene-dallalto/
Grazie
Sto andando avanti a piccoli sbuffi (Coriolis mi sta prendendo molto...).
Una possibilità empirica che butto lì è di continuare con la percentuale rimasta, facendo fermare il tutto quando è scesa sotto l'1%. A ogni passo si dimezza e il punto più importante è quando si arriva a 2 o a 4: in un modo o nell'altro si elimina la metà di quella che si sta considerando. penso non ci vogliano molti passaggi. Se riesco ci provo...
Ho fatto un calcolo veloce e sembra che debba aggiungere allo 0.125 un'altro 0.07... dovremmo essere intorno a 0.80 o poco meno... (sempre che non me ne sia dimenticato un po' per strada...).
Ciao Dany, la questione statistica e fortuna ( autopercepita) è trattata anche in questo articolo :
http://www.rivista.sis-statistica.org/cms/?p=532
In certo qual modo ci riporta alla serie di racconti sulle "credenze" e sul loro impatto sullo svolgimento degli avvenimenti.
In quanto al risultato del quiz, mi associo ai complimenti a Umberto per la scelta, e rilancio la domanda....
Non credete voi, gente di Teatro, che se il topo viene messo inizialmente nella cella numero 3 le sue probabilità di sopravvivere sono esattamente il 50 %.
E ancora, avete dubbi sul fatto che se lo metto nella cella numero 2 le sue probabilità aumentano al 75%, mentre se lo metto nella cella numero 3 calano al 25%?
Se nessuno mi risponde farò intervenire Oreste Pautasso, vedete voi cosa vi conviene....
Ben vengano le soluzioni alternative Vincenzo, ne sto studiando anche io un'altra; in quanto alla estensione di Maurizio aspetto anche io delle risposte, ma naturalmente non metto lingua..
No, no Pautasso no, per carità! È tempo di marroni, meglio che passi il tempo a raccoglierli e lasci in pace il topo di Umberdinger!!
Pautasso no, per carità! È tempo di marroni, meglio che passi il tempo a raccoglierli e lasci in pace il topo di Umberdinger!!
Per me le tue percentuali sono ad’OK, ma non ci metterei le mani sul fuoco (tanto non ce le ho )
)
Cari amici , vi posso dire che questa faccenda dei topi è molto popolare a Cuneo e dintorni.
L'esperienza dei nostri vecchi dice questo:
Se abbiamo N celle interposte tra quella dell'uscita e quella dove staziona il gatto famelico, e supponiamo che N sia un numero dispari, possiamo dire che mettendo il topo nella cella centrale la probabilità che si salvi è 0,5.
Se lo mettiamo nella cella immediatamente adiacente, più vicina alla salvezza, la sua probabilità di uscirne vivo diventa 0,5 + 0,5^2 = 0,75
Nella cella ancora adiacente e più favorevole la probabilità cresce di un valore = 0,5^3 , cioè diventa 0,75 + 0,125 = 0,875.
E così via, sommando ogni volta un valore 0,5^P dove P è la posizione dal centro ( considerato posizione 1).
La probabilità cresce progressivamente ( di un fattore sempre più piccolo) , quanto più il punto di partenza si sposta verso la cella della salvezza. Ovviamente la probabilità =1 non sarà mai raggiunta, per quanto ci si vada sempre più vicini.
Simmetricamente, nelle celle verso il gatto, abbiamo una curva speculare per la probabilità di essere trangugiato dal nemico, una distribuzione di probabilità complementare a quella associata alla liberazione
A Cuneo e dintorni abbiamo anche il calcolo per un numero N pari , ma non lo dico per lasciare il divertimento di scoprirlo a chi ne avesse voglia....
Se il ragionamento è sbagliato fatemelo sapere, ma vi assicuro che da noi funziona comunque.
Il valore finale è 0.75.
Basta risolvere l'equazione
50 + x + x = 100
2x = 100 - 50 = 50
x = 50/2 = 25
x è il numero di topi mangiati su 100. Il numero è lo stesso che si ottiene per i topi salvati dopo il pèrimo passo in cui se ne salvano 50.
Tra poco vi allego la figura in cui si disegna lo schema che serve a vedere l'uguaglianza tra topi mangiati e topi salvi. In realtà, chi comanda è la terza casella, chee smista i topi...
Ecco la figura che dimostra l'uguaglianza di x mangiati e liberi
veramente originale..e ormai bisogna svelare le carte.. La probabilità è proprio 0.75
questo non toglie che sono gradite altre soluzioni alternative. In ogni caso il quiz resta aperto fino alla soluzione che verrà data verso la fine della prossima settimana ( a dire la verità basterebbero i commenti)
Anche il grafico di Vincenzo porta alla probabilità di salvezza del topo del 75% .
La probabilità che il topo sia riuscito ad uscire (colonna 1) cresce a passi alterni.
Il primo passo contribuisce con il 50%. I passi dispari successivi contribuiscono con valori che sono potenze crescenti di 0,5 a partire da 0,125=0,5^3.
ormai non mi stupisco più di niente..un quiz così semplice con delle soluzioni alternative così originalmente costruttive e geniali..sono molto soddisfatto!
Ho provato a rappresentare il problema con una specie di albero che rappresenti il susseguirsi degli eventi con le rispettive probabilità ma sono andato a sbattere con il problema sollevato da Fabrizio. Quello cioe' della possibilita' di infiniti passaggi o di serie che non riesco a far convergere.
Scusa Vincenzo, perche' dici che i loop dovrebbero al limite portare a O ?
Grazie
Scusate non mi ero accorto che il dialogo era andato avanti
Caro Edoardo,
come vedi nella figura che ho inserito, ogni passaggio nel loop dimezza la percentuale e quindi un po' alla volta spariscono quelli in grado di ripetere il loop molte volte...
Certamente. Adesso SO'.Grazie
Il motivo per cui non si mette una bottiglia di eccellente barolo vicino al bordo del tavolo, ma piuttosto al centro, non è una questione di uguali opportunità per l'accesso alla risorsa, ma un accorgimento per massimizzare la probabilità che la bottiglia non cada dal tavolo.
Questa premessa, su cui credo Vincenzo potrebbe chiosare abbondantemente, spiega il motivo per cui, istintivamente, si tende a mantenere la maggior distanza possibile dall'area di rischio: è intuitivo ( e confermato dall'esperienza) che la probabilità di non subire danni aumenterà stando lontani dal pericolo.
Il topo del quiz non sa nulla del contesto in cui viene inserito. Non immagina che ci sia un gatto, né una via verso la libertà. Tuttavia, quando lo introduciamo nella sequenza delle celle, gli faremo correre meno rischi se lo terremo alla massima distanza possibile dalla cella del gatto.
Maggiore è il numero delle celle interposte e maggiore sarà la sua probabilità di uscirne vivo, come, nel caso della bottiglia, maggiore sarà il numero di centimetri di distanza dal bordo del tavolo e maggiore sarà la probabilità che non vada a frantumarsi sul pavimento.
Ora, venendo ai numeri, ho riprodotto la simulazione (complimenti per la trasmissione) di Vince, nel caso che le celle siano 5 (come previsto nel quiz) e anche nel caso che siano 6 oppure 7. In ciascuna situazione il topo viene immesso nella cella N2. Ovviamente, il numero di celle interposte tra lui e il gatto aumenta di caso in caso.
Dai risultati delle simulazioni, oltre alla conferma che la probabilità chiesta dal quiz è 0,75 (la convergenza a questo valore si verifica al passo 29), risulta che, con 6 celle, la probabilità di salvezza ( dopo 40 passi) sale a "quasi" 0,8 e con 7 celle, ancora meglio, arriva oltre 0,83.
I risultati di queste tre simulazioni confermano in parte quanto affermato da Oreste, anche se ridimensionano le probabilità a favore del topo. Oreste, infatti, prevedeva che il topo di Cuneo, immesso nella cella 2 di una sequenza di 7 celle, avesse una probabilità favorevole di 0,875, in base ad un calcolo evidentemente troppo "lineare", che va certo rivisitato in modo più rigoroso, tenendo conto delle regole del calcolo delle probabilità.
Nel prossimo commento i dettagli delle tre simulazioni...
Ecco i dettagli delle tre simulazioni:
Caso risolto da Vincenzo: topo in cella 2 - 5 celle totali - probabilità a favore 0,75 (29° passo)
https://s1.postimg.org/5m1neep6mn/simul_topo_5_celle.jpg
Caso di 6 celle - topo in cella 2 - probabilità a favore 0,7999 (40° passo)
https://s1.postimg.org/9ndruq43i7/simul_topo_6_celle.jpg
Caso di 7 celle - topo in cella 2 - probabilità a favore 0,8323 (40° passo)
https://s1.postimg.org/4g800263y7/simul_topo_7_celle.jpg
Maurizio,nella soluzione troverai la probabilità di salvezza espressa in funzione della distanza da salvezza e gatto..è una formula molto semplice!
Dite bene entrambi... D'altra parte più lontane sono le celle risolutive e maggiore è il numero per cui va moltiplicato 0.5 per se stesso (al primo passaggio) e via dicendo...
Beh... dateci qualsiasi fenomeno e saremmo in grado di parlarne per ore... Sono fiero di voi!!!! (mi ricordo anche il famoso gatto con il topo (o qualcosa del genere) e mi sembra di ricordare una trattazione e discussione analoga).
(mi ricordo anche il famoso gatto con il topo (o qualcosa del genere) e mi sembra di ricordare una trattazione e discussione analoga).
Certo che là al limite c'era solo il mio amicco gatto... adesso c'è anche il barolo e tutto diventa molto, molto più interessante
Aggiungo ancora: più sono le celle e più ci sono "loop" che, a bocce praticamente ferme, riducono le probabilità di cadere nelle grinfie del gatto. Ogni loop favorisce la salvezza (meglio aspettare...).
Belle simulazioni, fonte di ispirazione per trovare una semplice formula che dia subito il risultato...
Ad esempio, che ne dite di questa?
Probabilità salvezza topo = 1 - numero di caselle a sinistra / numero di caselle destra+sinistra
(la casella in cui si trova non entra nel calcolo)
Ad esempio il topo è nella casella 2 e le caselle sono 5. A sinistra ne ha 1 e a destra ne ha 3
Probabilità salvezza = 1 - 1/(1+3) = 1 -1/4 = 3/4 = 0,75
Altro esempio...
topo in casella 2 e 6 caselle. A sinistra ha 1 casella, a destra 4
Probabilità salvezza = 1- 1/(1+4) = 1-1/5) = 4/5 = 0,8
E così via... Come diceva quel Biellese di Aiazzone: "provare per credere" (Biella è a due ore di auto da Cuneo)
Cercando di essere ancora più semplici...
Probabilità salvezza topo = numero di caselle tra lui e il gatto (compresa quella del gatto) / numero totale delle caselle ( meno quella in cui si trova)
P.S. Per i più giovani ....La frase "provare per credere" era pronunciata, negli spot dei Mobili Aiazzone, da Guido Angeli e negli anni '80 era diventata un vero tormentone
Sapete cosa stavo pensando?
Tutti i quiz apparsi nel Circolo, soprattutto quelli che hanno visto una fattiva collaborazione, potrebbero essere messi in un vero libro (ed ebook) a nome di tutti i partecipanti. La spesa è insignificante e i pochi proventi potrebbero essere devoluti al sostenimento del blog (per adesso a carico del solo eroico Marko, alias SMA) e, nel caso, ad altre iniziative. Idem per astericcio e molto altro. Fare un libro con ilmiolibro della Feltrinelli è veramente semplice...
Ovviamente Scherzy e/o Daniela avrebbero un ruolo decisivo per dare ordine al tutto!!!!
Pensiamoci....
Secondo me, Enzone caro, hai confuso gatto e topo con volpe e coniglio... è forse questo il quiz a cui fai riferimento?
http://www.infinitoteatrodelcosmo.it/2016/12/04/quiz-la-volpe-e-il-coniglio-prima-parte/
Se qualcuno tra i neolettori (o tra gli affezionati che se lo sono perso o non hanno voluto provarci a suo tempo) ha voglia di provare a risolverlo, non ci farà che piacere!
Leggo ora l'ultimo commento di Enzone... e te' pareva che non mi trovasse qualcosa da fare, maremma papallina?!?
Comunque l'idea è buona, ma, per quanto riguarda Astericcio, manca almeno un raccontino piccino picciò (forse due...) prima di poter organizzare una raccolta che abbia un senso compiuto. Per i quiz si potrebbe già fare, parliamone!
Per il sostentamento del blog, non preoccuparti, i fondi arrivano già da Papalla e sono veramente pochi quelli necessari, un'eventuale raccolta potrebbe essere destinata ad una causa più nobile: per decidere quale potremmo sceglierne qualcuna e chiedere ai nostri lettori di votare. Dopodiché, ovviamente, renderemo periodicamente pubbliche le ricevute di versamento... cosa ne pensi?
Sicuramente d'accordo. Ricorda però che sono pochi spiccioli... Non siamo un calciatore che parla della sua carriera...
Lo so, lo so...
"Quello che noi facciamo è solo una goccia nell'oceano, ma, se non lo facciamo, quella goccia mancherà per sempre" (Madre PapalTeresa di Calcutta)
Pubblichiamo, pubblichiamo, che gli italiani sappiano e il mondo ricordi !
Tanto per concludere la questione del roditore e del felino..... Da quanto ho (faticosamente) capito leggendo l'ultimo commento di Oreste, direi che:
Se le celle, in totale, sono N (con la cella 1 a sinistra, verso la libertà) in essa la probabilità di salvezza sarà =1.
Posizionando il topo in questa prima cella siamo certi di salvarlo.
Se lo posizioniamo nella cella 2 la probabilità a suo favore diminuirà di un fattore = 1/(N-1) e la stessa diminuzione l'avremo, di cella in cella, andando verso il gatto
quindi nella cella 2 (con N = 5 ) avremo 1-1(4) = 3/4 = 0,75 (proprio il risultato da trovare)
nella cella 3 ............. 2/4 = 0,5 ( logico, data la simmetria)
nella cella 4 .............. 1/4 = 0,25 ( speculare alla cella 2)
nella cella 5 .............. 0/4 = 0 (il gatto non perdona)
E se le celle fossero 6 ?
Allora avremmo, in modo analogo:
cella 1 P= 5/5 = 1
cella 2 P = 4/5 = 0,8
cella 3 P = 3/5 = 0,6
cella 4 P = 2/5 = 0,4
cella 5 P= 1/5 = 0,2
cella 6 P = 0/5 =0
Ma è davvero possibile che sia così semplice...?
Dunque...
continuo sulla strada geometrica...
chiamiamo LOOP la figura romboidale in neretto nella figura che segue.
Nel caso in questione, le probabilità di essere mangiato sono date dalle rette inclinate che finiscono in 5. (morte diretta). Poi ci sono le morti ritardate, dopo che il topo ha fatto un LOOP. Esse partono sempre dalla 2 e finiscono nella 5. I LOOP continuano e ognuno ha il vertice superiore che è moltiplicato per 0.5 rispetto a quello inferiore. Facendo tendere i loop a infinito avremo il risultato finale. Fin qui penso di seguire l'approccio di Fabrizio...
Se cresce il numero di celle aumentano le colonne di LOOP. Ne segue che da un lato si sommano le probabilità di essere mangiati (loop che portano alla morte),ma queste si riferiscono a loop sempre meno ricchi di probabilità, per cui al crescere delle colonne di loop chi vince è la probabilità di fuga.
In questo modo, penso che si possa "facilmente" spostare la colonna di partenza... (vedi Oreste).
Insomma, non credo di essere stato chiaro, ma vado di corsa. Il succo è legato solo e soltanto alle colonne di loop e alla posizione di partenza.
il gioco continua con mia grande soddisfazione..cerchiamo proprio una relazione fra la posizione iniziale e il numero di celle..
scusate , ho paura di non essere stato abbastanza chiaro: Una relazione fra la probabilità di salvezza in funzione del numero di celle e della posizione iniziale
Allora, Umberto, dopo varie simulazioni con l'algoritmo di-Vino Vincenziano, sono giunto alla conclusione che l'espressione che esprime la "relazione fra la probabilità di salvezza in funzione del numero di celle e della posizione iniziale" è la seguente....
Probabilità di salvezza = ( Numero di celle - Posizione iniziale) / (Numero celle -1)
definendo: Probabilità di salvezza = P Numero di celle = N Posizione iniziale = I
P = ( N-I)/ (N-1)
Constatato ma non (ancora) dimostrato analiticamente.
ok, prendo nota..ma dovrai aspettare la soluzione perché il nuovo problema è ancora sperto
Ricopio di seguito il primissimo commento postato da Andy...
Buonasera Umberto,
il mio ragionamento è questo:
il topo ha 6 possibilità di stazionamento complessivamente, 5 scatole + l'uscita:
se, in un determinato momento si trova nelle scatole 1, 2, 3, 4, o all'uscita, si salva;
se, in un determinato momento si trova nella scatola 5, non si salva;
la probabilità di salvarsi dovrebbe essere 5/6;
la probabilità di non salvarsi 1/6"
Proverei a riformularlo in questo modo.....
Delle 5 caselle (N) , togliendo quella che occupa , il topo ne ha 4 a disposizione (N-1)
Di queste 4 caselle quelle "importanti" sono quelle che lo distanziano dal gatto (N-I)
Il rapporto tra il numero di caselle "distanziatrici" e quelle disponibili è la probabilità di salvezza.
Nel caso del quiz N=5 , I=2 , caselle "distanziatrici" = N-I = 5-2 = 3 caselle disponibili = N-1 = 5-1 = 4
Probabilità salvezza = 3/4 = 0,75
Per semplificare le formule ribalto la numerazione delle scatole data da Umberto nella definizione del quiz (figura sotto). Chiamo 0 quella del gatto e numero le scatole a partire da quella. Il topo sarà libero se raggiunge la scatola che numero genericamente con N. Nel quiz iniziale N=4. Una scatola generica intermedia avrà come numerazione un intero i compreso tra 0 e N.

Con la numerazione delle celle data sopra, la probabilità chiesta da Umberto è i/N. Dovrebbe coincidere numericamente con quelle trovate da Maurizio con le simulazioni. Provo a dare un giustificazione a questo risultato.
Riprendo quanto ho scritto in un post precedente. Per come è definito il comportamento del topo nel quiz, queste probabilità non dipendono da come il topo è arrivato ad una delle caselle. Questo mi permette di mettere in relazione queste probabilità limitando il ragionamento ai soli percorsi fino alle caselle adiacenti.
Suppongo di non conoscere S(i), ma di conoscere le probabilità di salvezza del topo quando si trova nelle celle adiacenti (S(i+1) ed S(i-1)). Da queste due probabilità è possibile calcolare S(i)?
Partendo dalla scatola i, il topo come può raggiungere la libertà?
Nel 50% dei casi va verso la scatola i+1 dove ha probabilità di salvezza S(i+1) e nell'altro 50% va nella scatola i-1 dove ha probabilità di salvezza S(i-1). Metto insieme le due possibilità ed ottengo che la probabilità di raggiungere la salvezza per un topo nella scatola i:
S(i)=0,5 S(i+1)+ 0,5 S(i-1).
Quindi S(i) coincide con la media aritmetica tra le due probabilità di salvezza delle celle adiacenti ed è numericamente equidistante tra le probabilità (S(i+1)-S(i)=S(i)-S(i-1)). Questo vale per tutte le celle essendo i generico.
Ne segue che la differenza tra le probabilità di salvezza del topo per due celle adiacenti è 1/N e le probabilità sono quelle nella figura sotto. Andando verso sinistra si aggiunge 1/N alla probabilità precedente fino ad arrivare all'ultima cella dove è 1.
Nel caso del primo quiz N=4, le probabilità di salvezza del topo erano S(3)=3/4, S(2)=2/4, S(1)=1/4. Ricordo che qui la numerazione è invertita rispetto a quella data da Umberto nella definizione del quiz.
Altri esempi numerici sono quelli fatti da Maurizio.
Mentre Fabrizio scriveva il precedente commento ho tracciato questo grafico....
https://s1.postimg.org/7bn4p168xr/probailit_e_passi.jpg
La crescita della curva , fino ad arrivare al valore 0,75 avviene precisamente secondo la formula già contenuta in un precedente commento di Fabrizio:
"Il primo passo contribuisce con il 50%. I passi dispari successivi contribuiscono con valori che sono potenze crescenti di 0,5 a partire da 0,125=0,5^3.
Nel caso che il topo sia immesso nella casella 3 la curva ha lo stesso andamento, cioè la sommatoria è identica, ma il valore iniziale, invece di 0,5 è 0,25, con il risultato che la probabilità diventa =0,50
Analizzando il caso di 6 celle (invece di 5) e posizione iniziale del topo nella cella 2, si arriva a questo grafico...
https://s1.postimg.org/8pc7op9wlr/probabilita_e_passi_2.jpg
L'aspetto è molto simile a quello del precedente commento, ma la composizione dei vari contributi, passo dopo passo, non è, ovviamente, la medesima, Il dato iniziale è sempre = 0,5 ma, nella sommatoria, a partire dal terzo elemento in poi i valori sono maggiorati rispetto a quelli del caso precedente, penso per l'interferenza della "riflessione"nei percorsi delle celle interne ( ora sono in numero maggiore). La composizione appare abbastanza complessa e destinata a complicarsi ulteriormente al crescere del numero delle celle che compongono il sistema.
Umberto, quando dici...
"il nuovo problema è ancora aperto"
Intendi dire che si deve cercare una spiegazione.alternativa del risultato ?
Potresti enunciare esplicitamente la domanda a cui si deve rispondere?
niente di specifico. Quello che state cercando tu e fabrizio
Un pensiero mattutino.... Il Reticolo Dicotomico Zappaliano ( RDZ) genera, in corrispondenza delle celle agli estremi sinistro e destro, le relative probabilità di salvezza del topo e di soddisfazione del gatto.
Sono ambedue numeri razionali, che derivano dal rapporto di numeri interi ( caselle).
L'accumulo, che a passi alterni, porta a crescere queste due probabilità, costituisce una serie, a segni positivi, ( o una combinazione di più serie) che tende al valore del numero razionale corrispondente.
La domanda che mi pongo è come è composta, in generale, questa serie che converge (forse andrebbe dimostrato che è convergente) al numero razionale.
Due esempi già li abbiamo, quelli che ha trovato Fabrizio e che ho citato nel precedente commento, ma poi ?
Breve analisi circoscritta al confronto tra circuito di 5 celle e circuito di 6 celle , limitatamente ai primi 7 passi.
https://s1.postimg.org/7x3ouhs8xr/simulazione_3.jpg
Estendendo il ragionamento potremmo dire nel caso di 6 celle al passo 7 (= numero celle +1) si deve aggiungere un contributo (dovuto proprio alla cella in più) pari a 100*0,5^7 ( 7 è il passo corrente).
Verrebbe da dire che il ragionamento vada iterato per i passi successivi. Occorre trovare una generalizzazione.
Giuro che dopo questo commento me ne starò quieto ( almeno per un po')...
Non aggiungo altre figure, ma avendo esaminato i passi successivi al settimo, ne ho tratto la sensazione che i fenomeni di "riflessione" che nascono quando si aggiunge la cella numero 6, vanno sovrapponendosi come "echi multipli".
Procedendo con i passi successivi, il contributo aggiuntivo ad ogni passo è composto da frammenti sempre più piccoli e sempre più numerosi, effetto ritardato delle riflessioni "fossili" precedenti.
Comunque, mi sembra che lavorare su queste considerazioni, tese a collegare il risultato finale della probabilità alla sequenza dei flussi delle migrazioni topesche, sia un po' come voler esprimere la temperatura in funzione della valutazione delle energie delle singole molecole.
Aggiungo solo l'ultima immagine che forse chiarisce meglio cosa intendevo dire....
https://s1.postimg.org/828und6t9r/simulazione_4.jpg
Solo un accenno ai loop... per rispondere anche a Mau.
A mano a mano che aumenta il numero di celle (ma lascio fissa la 2 come inizio), rimane valida (penso) l'uguaglianza tra topi che scappano e topi che si salvano, ma, aumentando le celle questa uguaglianza si sposta sempre verso l'alto del mio digramma. Se con 5 celle va aggiunto 0.5 a 2n, con 6 celle forse bisogna aggiungere 0.5 + 0.125 e via dicendo...
0.50 + n + n = 1
0.50 + 0.125 + n + n = 1
Ma non ho avuto tempo per verificare... questa volta per colpa di Foucault e del suo specchio girevole...
Grazie Vincenzo per il commento su cui rifletterò, Nel frattempo ho prodotto questo disegno che illustra come si compongono le riflessioni.
Siamo nel caso di 6 celle e di posizionamento iniziale in cella 2.
Ad ogni passo il contributo delle riflessioni multiple giunge attraverso percorsi che vanno crescendo di numero, via via che considero passi successivi.
Il problema di conoscere l'entità dell'incremento della probabilità ad ogni passo si riconduce "semplicemente" a valutare il numero di cammini alternativi che, per quel passo, sono disponibili alle riflessioni.
I cammini alternativi al passo 7 sono solo 5, già al passo 9 diventano 13.
Comunque il calcolo dei cammini alternativi dovrebbe essere l'ultimo scoglio verso una formulazione precisa, e credo sia un calcolo affrontabile. Andiamo avanti?
caro Mau,
i percorsi possono essere classificati di tre tipi: a, b e c (nel caso di 6 celle se no crescono di conseguenza).
Il tipo a si svolge solo tra 2 e 1 (il zig zag rosso), il tipo b, si svolge tra 3 e 1 (zig zag verde), il tipo c tra 4 e 1.
I topi che si liberano provengono solo e soltanto da questi percorsi di diverso peso probabilistico.
Il primo passo libera solo i rossi (50 su 100)
il secondo solo verdi e rossi
dal terzo in poi tutti e tre i tipi....
basta sommarli?
Penso che i zig zag intermedi siano già contati in questo schema...
Boh... se lo trovate utile... io torno a Foucault...
Ho analizzato in dettaglio il caso delle 5 celle, proposto nel quiz.
I topi in uscita arrivano a ondate, nei passi dispari, a partire dal primo.
Ad ogni ondata corrisponde un grafo orientato dalla cella di partenza ( la 2 ) alla cella di uscia (la 1) , scendendo, passo dopo passo.
La complessità del grafo aumenta progressivamente ad ogni passo, per il numero di nodi e di archi.
Il grafo completo rappresenta tutti i possibili percorsi, sempre dello stesso numero di archi e di nodi in cui si verificano le biforcazioni.
Il numero di "varianti" rappresenta tutti i percorsi distinti, estraibili dal grafo, che convergono all'uscita per formare l'ondata.
Nel caso di 5 celle il calcolo delle varianti è semplice, pertanto si possono calcolare tutti i valori in corrispondenza alle ondate di uscite, per ciascun passo.
Questa è la figura che illustra il concetto delle ondate di uscita per il caso delle 5 celle, con posizione iniziale 2.
Sto studiando l'estensione al caso in cui le celle sono 6. La logica è la medesima ma la geometria del grafo è più complessa a causa della cella in più.
Ecco il grafo corrispondente al precedente, nel caso di 6 celle (anche qui limitatamente alle prime 5 ondate).
Le losanghe riempite di colore azzurro rappresentano l'espansione dei grafi resa possibile dalla cella in più.
Questa espansione determina un numero di nodi e di archi maggiore e quindi un numero di varianti maggiore estraibili dal grafo. In definitiva avendo più possibili percorsi aumentano le quantità in uscita a ciascun passo.
Il calcolo del numero di varianti è più complesso del caso con 5 celle
In quel caso il numero delle varianti, per le ondate successive alla prima valeva V(s) = 2^ ((s-3)/2), ove "s" è il numero di step in cui si verifica l'ondata.
Si tratta ora di trovare l'espressione generale del numero delle varianti nel caso delle 6 celle e posizione iniziale nella cella 2.
Se non ho sbagliato le mie valutazioni per i grafi successivi, il numero di varianti cresce molto rapidamente: ala sesta ondata (passo 11) le varianti dovrebbero essere 34, alla settima ondata (passo 13) dovrebbero essere 90 e alla ottava ondata (passo 15) potrebbero essere 232...
Successivamente si potrà generalizzare il calcolo per un qualsiasi numero di celle e una qualsiasi posizione iniziale del topo, ma questa è un'altra faccenda.
Scusa Mau, sei sicuro di non essere caduto in un loop "grafomane" senza via d'uscita?!?

Umberto, per favore, dai la soluzione così il povero Mau potrà riprendere il suo tranquillo tran tran quotidiano da ingegnere pensionato...
Caro Scherzy, forse non lo sai, ma Umberto ha un bellissimo supergatto di 7 chili. E' lui che ha commissionato il quiz ed è molto, molto interessato a conoscere tutti i particolari sulla dinamica della fuga dei topi. Penso che deciderà lui quando sarà il momento di dare la soluzione...
Ahi ahi ahi... la conoscenza da parte del supergatto della dinamica della fuga dei topi altererà i risultati che darà Umberto... a quel punto dovrai iniziare da capo con altri loop grafomani che tengano conto di questa mutata ed imprevedibile situazione temo che non ce la farai a tornare in tempi brevi a leggere il giornale sulle panchine
temo che non ce la farai a tornare in tempi brevi a leggere il giornale sulle panchine 
in ogni caso il topo é morto di vecchiaia..é meglio che ci spostiamo verso il nastro di Mobius..
Questo è il mio ultimo post sul tema gatto-topi. Ormai la costruzione è evidente e chi vuole può sbizzarrirsi a estendere ulteriormente il modello.
La figura, relativa a una batteria di 6 celle, illustra il grafo e il calcolo per valutare le uscite della sesta ondata.
Un dettaglio che illustra l'individuazione delle 8 varianti nel subset del grafo che arriva alla casella 6.4
Adesso posso dedicarmi al giornale, non tanto per leggerlo sulla panchina, come insinua Scherzy, ma per ricavarne delle interessanti striscioline di carta, che potranno essere più utili delle (cattive) notizie riportate nel quotidiano, al fine di rilassarsi con un nuovo quiz. Proprio quello a cui accennava Umberto.