Categorie: Fisica classica
Tags: indice di rifrazione ottica geometrica principio di Fermat QED riflessione rifrazione
Scritto da: Vincenzo Zappalà
Commenti:4
Il principio di Fermat e i percorsi della luce **
Abbiamo parlato varie volte del percorso della luce, sia dal punto di vista puramente geometrico sia attraverso la teoria ondulatoria, per non dire poi della fantastica teoria di Feynamn (la QED). Abbiamo, però, quasi sempre accettato le due leggi più celebri dell'ottica geometrica (tranne che nella QED): la riflessione e la rifrazione. Vale la pena di dare un po' più di spazio all'ottica geometrica che è pur sempre utilissima per descrivere i cammini ottici e schematizzare ciò che capita nei prismi, nelle lenti, nei telescopi e cannocchiali vari.
Quello che faremo è molto semplice: partiremo dal principio di Fermat e dimostreremo perché la luce si riflette e si rifrange in un certo modo. Niente di veramente speciale, ma un bell'esercizio che si ricollega allo studio di funzioni e, in particolare, alle derivate.
Il principio di Fermat (1601-1665) dice molto semplicemente:
"Un raggio luminoso tra due punti segue il percorso a cui corrisponde il minor tempo di percorrenza."
Notiamo bene che non si parla di PERCORSO MINIMO, ma di TEMPO DI PERCORRENZA MINIMO. Possiamo facilmente ricavare le leggi della riflessione e della rifrazione partendo solo dalla definizione di Fermat.
RIFLESSIONE
Immaginiamo di far partire un raggio luminoso da un punto P e volerlo ricevere nel punto R, dopo avergli fatto toccare la superficie completamente riflettente S. Ovviamente, vi sono infinite possibilità teoriche, come mostra la Fig. 1.
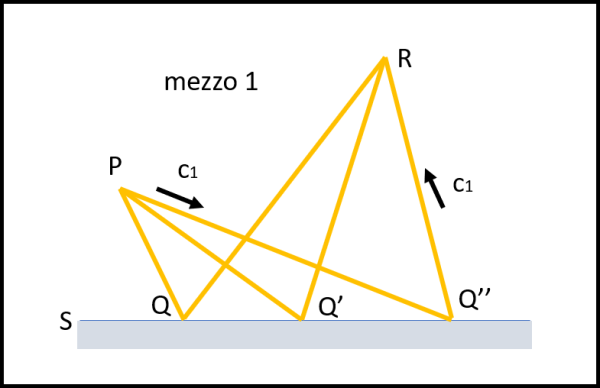
Noi , però, ci basiamo solo e soltanto sul principio di Fermat e non proviamo assolutamente a cercare il percorso più corto, ma solo il più veloce. Non ridete... cerchiamo di descrivere il tutto nel modo più rigoroso possibile.
Il tempo speso dalla luce per andare da P a R, toccando S, è legato ovviamente alla velocità della luce c, che può esprimersi come spazio diviso tempo. Teniamo anche conto che la velocità della luce dipende dal mezzo in cui si propaga, seguendo la relazione
cm = c/nm
dove c è la velocità della luce nel vuoto, cm quella nel mezzo in cui si propaga e nm l'indice di rifrazione del mezzo, valore che è sempre maggiore di 1 e vale 1 nel caso del vuoto. In poche parole, maggiore è l'indice di rifrazione e minore è la velocità della luce (ricordiamo, comunque, che la QED affronta la situazione in modo sostanzialmente diverso).
Per il nostro scopo dobbiamo esprimere, perciò, il tempo impiegato per ogni percorso in funzione del cammino percorso, ossia t = f(x) dove x è la lunghezza misurata sull'asse coincidente con la superficie dello specchio visto di taglio. Possiamo risolvere il problema in due dimensioni. in quanto il cammino della luce avviene su un piano (quello del foglio nel nostro caso). Consideriamo la Figura 2, dove è stato scelto un percorso qualsiasi, assumendo che la luce viaggi sempre in linea retta. D'altra parte, per il principio di Fermat, il raggio che va da P al punto dello specchio scelto (Q) deve scegliere il percorso eseguito nel tempo minore, ossia quello rettilineo (lo stesso deve anche capitare per il tratto tra Q e R).
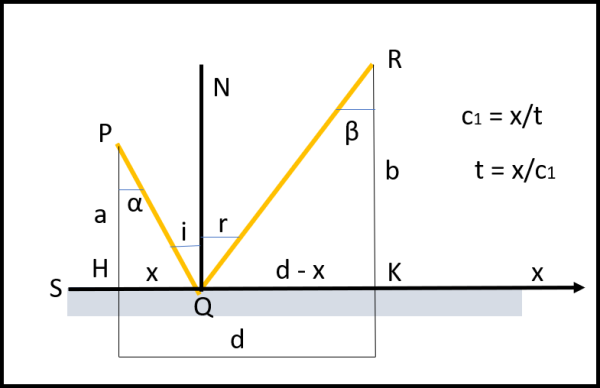
Scriviamo allora il tempo impiegato per andare da P a Q e poi quello impiegato per andare da Q a R, ponendo la distanza tra HK, lungo l'asse x, uguale a d e le distanze di P e Q dall'asse x, uguali ad a e a b (PH e RK), rispettivamente. Il mezzo in cui si svolge il percorso è sempre lo stesso (1) e quindi è sempre la stessa anche la velocità della luce c1. Attraverso il teorema di Pitagora applicato ai triangoli PHQ e RKQ
tPR = tPQ+ tQR = PQ/c1 + QR/c1 = 1/c1 (√(a2 + x2) + √(b2 + (d - x)2)) .... (1)
Per trovare il tempo minore basta calcolare la derivata di (1) e uguagliarla a zero:
t'PR = 1/cm(x/(√(a2 + x2) - (d - x)/√(b2 + (d - x)2)) = 0 .... (2)
Ricordiamo, per i meno esperti, che la derivata di √(f(x) vale f'(x)/2√f(x)
Utilizzando un po' di trigonometria è facile scrivere, relativamente ai triangoli rettangoli PHQ e RKQ:
HQ = PQ sen α
KQ = RQ sen β
e ancora:
HQ/PQ = sen α = x/√(a2 + x2)
KQ/RQ = sen β = (d - x)/√(b2 + (d - x)2) .... (3)
Sostituendo le (3) nella (2) si ottiene
1/c1(sen α - sen β) = 0
Dato che 1/c1 non può mai essere zero, l'unica soluzione possibile è:
sen α - sen β = 0
sen α = sen β
Ma α = i e β = r (alterni interni di rette parallele tagliate da una trasversale), per cui:
sen i = sen r
i = r
Il percorso di tempo minore è quello in cui l'angolo di incidenza i ( tra il raggio incidente e la perpendicolare allo specchio in Q) è uguale all'angolo di riflessione r (tra il raggio uscente e la perpendicolare allo specchio in Q).
Notiamo che la velocità è sempre la stessa (il mezzo è sempre lo stesso) e che quindi il percorso di tempo minore coincide con quello di minore distanza.
RIFRAZIONE
In questo caso, ciò che vogliamo fare è trovare il percorso di tempo minimo tra il punto P e il punto R, che si trovano immersi in due mezzi diversi (1 e 2). Il che vuole dire che c1 ≠ c2. Utilizziamo la Fig. 3, dove si può notare che i percorsi sono infiniti, ma che il problema è accentuato dal fatto che la luce viaggia più piano in un mezzo piuttosto che nell'altro.
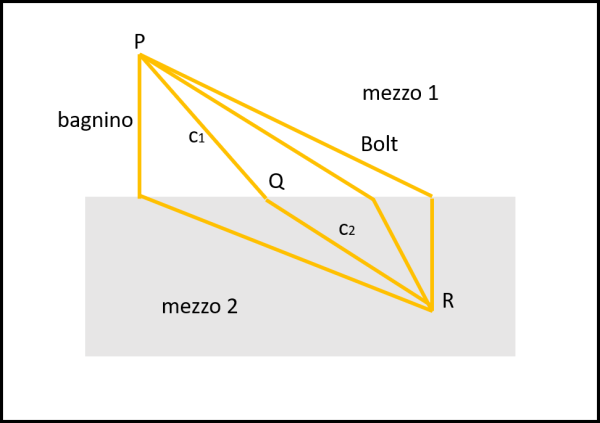
Il problema può essere reso molto pratico pensando che il mezzo 1 sia la sabbia e il mezzo 2 sia l'acqua, in una spiaggia alla moda, molto affollata. Poniamo che P sia un bagnino e che R sia un bagnante in difficoltà. Se il bagnino è un nuotatore formidabile la sua velocità potrebbe essere maggiore in acqua che sulla spiaggia. Lui potrebbe scegliere di andare direttamente verso la spiaggia e poi nuotare nel tratto più lungo. Sempre in P, però, vi è anche Usain Bolt, il quale parte insieme al bagnino per dare il suo aiuto. Lui, però, preferisce percorrere sulla spiaggia il tratto più lungo e poi nuotare per il tratto più corto. Nel nostro caso, però, il "salvatore" è la luce che viaggia decisamente più piano nel mezzo 2. In generale, considerando due mezzi qualsiasi, se c è la velocità della luce nel vuoto, abbiamo che:
c1 = c/n1
c2 = c/n2
dato che n2 ≠ n1, risulta c1 ≠ c2.
Affrontiamo il problema utilizzando la Fig. 4 dove è stato inserito un tragitto qualsiasi.
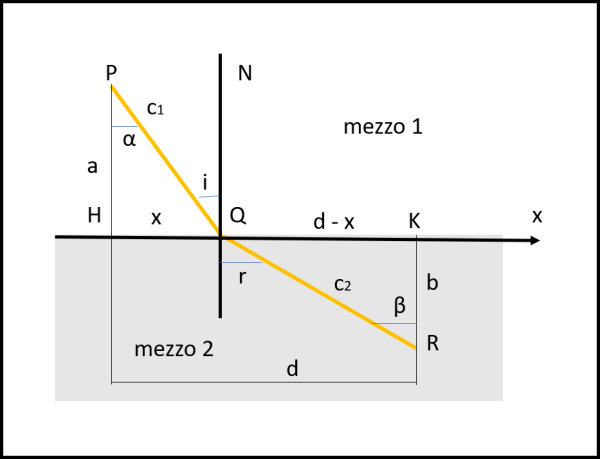
Possiamo già concludere, però, che il percorso di minima distanza (ossia la congiungente P con R) non potrà essere il percorso di tempo minimo (dato che c1 ≠ c2) . Usiamo le stesse notazioni della Fig. 2 e scriviamo il tempo necessario ad andare da P a Q e da Q a R, tenendo conto che c1 ≠ c2:
tPR = tPQ+ tQR = PQ/c1 + QR/c2 = (√(a2 + x2)/c1 + √(b2 + (d - x)2))/c2
e poi eseguiamo la derivata e ponendola uguale a zero:
t'PR = (1/c1)(x/(√(a2 + x2)) - (1/c2)(d - x)/√(b2 + (d - x)2)) = 0
Come nel caso della riflessione possiamo scrivere:
x/(√(a2 + x2) = sen α
(d - x)/√(b2 + (d - x)2) = sen β
da cui:
t'PR = sen α/c1 - sen β/c2 = 0
Ossia, ricordando che cm = c/nm:
sen α/sen β = c1/c2 = n2/n1
O, ancora:
sen i/sen r = n2/n1
Il che vuole dire che passando da un mezzo con indice di rifrazione minore (n1) a uno con indice maggiore (n2), l'angolo di incidenza i è maggiore dell'angolo di rifrazione r e viceversa.
Questa situazione è conosciuta molto bene dal nostro pesce scaltro (QUI)






4 commenti
Buongiorno, argomento interessante e ben argomentato, mi chiedevo come interpretare il Principio di Fermat nel caso in cui il punto finale fosse S, in un mezzo 3 ?
Un po’ empiricamente penso di risolvere il problema applicando le formule trigonometriche
sen i/sen r = n2/n1
sen i_2/sen r_2 = n3/n2
Naturalmente non potendo sapere quale sia il primo angolo di incidenza, faccio finta che esso abbia vertice in Q’ punto di intersezione tra la retta PS (percorso di minor spazio) e la linea di separazione tra mezzo 1 e mezzo 2, e risolvo le equazioni trigonometriche.
A questo punto, dato che il raggio finale "non giunge" nel punto predetto S (pur se ottenuto nel rispetto della legge Trigonometrica esposta), aumento con piccoli incrementi il primo angolo di incidenza, fino a quando non ottengo un valore tale che il percorso tra P ed S, nei tre mezzi , risulta di minor tempo!
Analiticamente invece che tipo di approccio al problema si potrebbe avere (nel caso il percorso preveda un punto S da raggiungere in un terzo mezzo)? Immagino si debba porre a zero la derivata del tempo , ma qui abbiamo...tre tempi di percorrenza.
Dan
caro Dan,.
non è facile spiegare nella risposta a un commento. Tuttavia, basta pensare che, conoscendo il punto iniziale e quello finale ,è possibile eseguire la prima e seconda rifrazione in termini generali e poi trovare la soluzione che ha in comune il punto intermedio..
Grazie, buone Feste Pasquali !