Questo articolo è stato inserito nella pagina d'archivio dedicata all'Ottica, in Fisica Classica.

Questo articolo è una delle tante "ciliegine cosmiche" che potete gustare QUI

 

La legge della riflessione luminosa è quanto di più semplice si possa immaginare, eppure è capace di trarre in inganno altrettanto facilmente.

Uno specchio piano non inverte un bel niente (o quasi...)

Quante volte abbiamo sentito dire che uno specchio inverte la destra con la sinistra, mentre - stranamente- non inverte l'alto con il basso? A prova di tutto ciò si usa spesso scrivere una parola su uno pezzo di carta e poi mostrala allo specchio: la scritta appare invertita un bel CIAO diventa uno strano OAIC.

Bene, tutto ciò non è assolutamente vero! Lo specchio non inverte assolutamente la destra con la sinistra, ma praticamente ci fa entrare in un mondo separato, quello delle immagini. E' un po' come si riuscisse ad andare dietro allo specchio e vivere in un mondo creato dal nulla.

Per mostrare che non vi è nessuna inversione, ma solo una RIFLESSIONE, vengono spesso usate tante parole che, a volte confondono di più invece di chiarire. Io preferisco utilizzare dei disegni che, immediatamente, risolvono la faccenda in modo lampante.

Cominciamo con la Fig. 1, dove abbiamo disegnato lo schema di noi stessi con testa T e piede P.

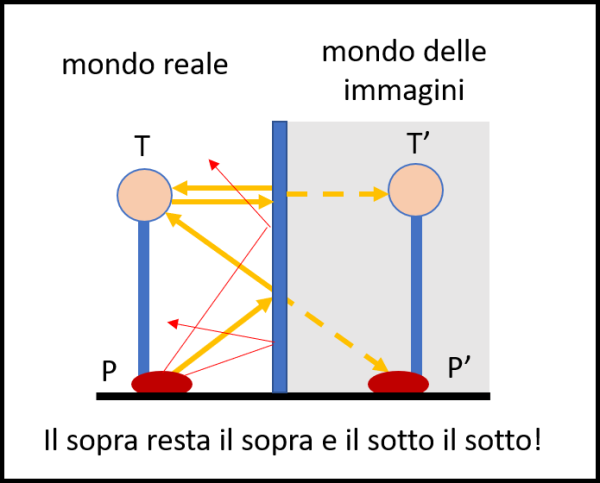
Ciò che comanda tutto è il nostro occhio. Per potere vedere qualcosa è necessario che un raggio luminoso parta da una certa sorgente e arrivi all'occhio di chi guarda. La QED illustra in maniera magnifica come tutto ciò avvenga nel mondo misterioso della Meccanica Quantistica, ma noi ci limitiamo a una trattazione puramente geometrica, più che sufficiente per spiegare l'intera faccenda.

Davanti a noi (TP) poniamo uno specchio riflettente. Facciamo partire i raggi luminosi dal piede P. Ne partono tantissimi in ogni direzione, ma a noi interessa solo e soltanto quello che dopo aver colpito lo specchio, essersi riflesso attraverso la legge della riflessione, giunge al nostro occhio che facciamo coincidere con T. Ovviamente, i raggi rossi sottili non ci interessano perché si riflettono e se ne vanno per la loro strada. Il raggio importante è quello giallo spesso. Lui parte dal piede P tocca lo specchio e viene riflesso come tutti facendo lo stesso angolo con la perpendicolare allo specchio di quello fatto dal raggio incidente (legge della riflessione). Questo raggio va a colpire l'occhio posto in T. La luce del piede è arrivata all'occhio, ma l'occhio dove la vede? Non può che vederla luno la linea retta che lo ha colpito (la luce viaggia in linea retta) e quindi basta prolungare il raggio incidente fino a che non colpisca il suolo in P'. Poco importa che questo punto esista in un altro mondo, quello delle immagini, che sembra esistere in un luogo impossibile, ossia dietro allo specchio... Questa è la realtà dei fatti.

Essendo un circolo astronomico, possiamo fare un paragone con la luce di una galassia lontana che passa al bordo di una galassia più vicina e viene deviata a causa dell'effetto  lente gravitazionale causato dalla massa della galassia in primo piano. Il raggio devia il suo percorso e invece di andare per i fatti suoi viene proprio a cadere sul nostro telescopio (e quindi sul nostro occhio). Per noi (e per il nostro telescopio) la galassia lontana viene a trovarsi lungo il prolungamento del raggio che ci ha colpito, ossia in una posizione diversa da quella reale, come mostra la Fig. 2.

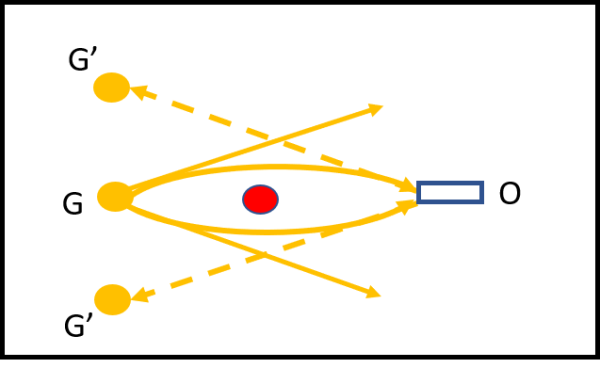
La posizione reale  della galassia lontana è G, mentre quella che vediamo noi è G'. Vediamo un'immagine che non coincide certo con la sorgente, dato che è dovuta passare attraverso una lente ... gravitazionale, al pari di una lente vera e propria. L'unica differenza con il caso dello specchio è che la lente cambia la direzione della sorgente, ma essa resta nel mondo "reale", mentre lo specchio la porta in un mondo apparente e irraggiungibile.

Torniamo alla Fig. 1. Cosa succede , invece, al raggio che parte da T. Esso viaggia orizzontalmente, colpisce lo specchio e torna esattamente indietro lungo la direzione di invio. A T appare un' immagine T' che sta proprio sulla direzione di partenza e di ritorno. Anch'essa, tuttavia, è un'immagine che vive nel mondo nascosto e irraggiungibile dello specchio. In ogni modo, ciò che succede è che il nostro occhio vede un'immagine di noi stessi con i piedi in basso e la testa in alto. Non vi è nessun capovolgimento!

Disegniamo adesso la stessa situazione vista dall'alto (Fig. 3).

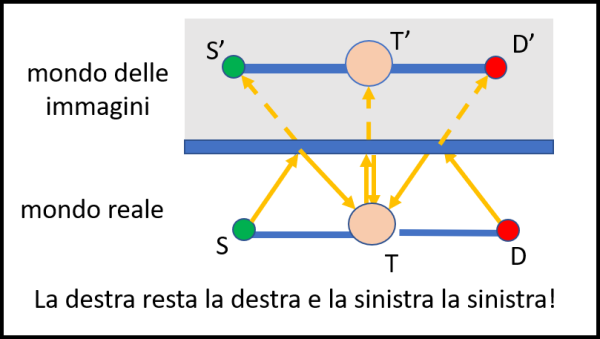
Noi siamo rappresentati con la solita testa in T e con le due braccia distese, con la mano destra D colorata in rosso e con la sinistra S colorata in verde. Cosa succede alla luce che parte da S. Il raggio che interessa è, come sempre, quello che si riflette e colpisce il nostro occhio. Prolungando il raggio di ritorno, la mano sinistra crea l'immagine in S'. Analogo procedimento per la mano destra. Cosa è successo? Esattamente quanto è capitato per la testa e i piedi. La mano destra resta alla nostra destra e la mano sinistra alla nostra sinistra! E' solo il nostro cervello che vedendo la nostra immagine riflessa conclude che la mano destra sia passata a sinistra e viceversa. Il nostro cervello pensa che noi ci sia spostati nel mondo delle immagini, dove dovremmo girare di 180 gradi per assumere la posizione dell'immagine, ma ciò non è assolutamente vero.

Possiamo confermare il tutto scrivendo su un foglio la parola CIAO. La faccia del foglio anteriore con scritto CIAO la vediamo direttamente e leggiamo le lettere da sinistra a destra (Fig. 4).

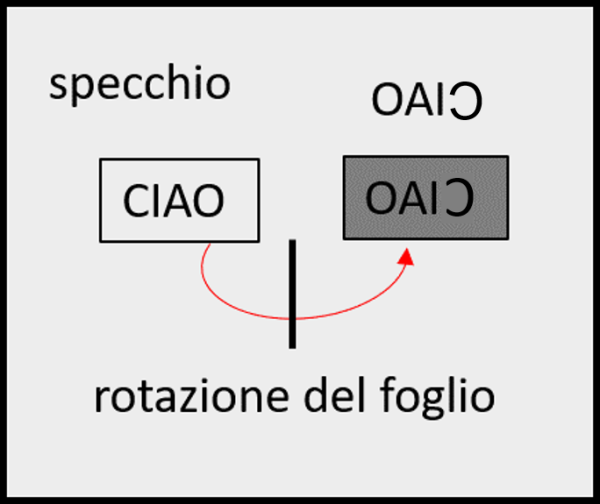
Tutto OK. Poi, cosa facciamo per vedere l'immagine riflessa del foglio? Ruotiamo il foglio di 180° rispetto a noi. Facendo questa operazione, la faccia del foglio che vediamo è quella  posteriore. Potessimo vedere attraverso il foglio, leggeremmo OAIC, che è proprio quello che viene riflesso nello specchio. Per vedere le lettere al contrario abbiamo dovuto girare il foglio di 180°. Proprio la rotazione che il nostro cervello ha "immaginato" guardando la nostra immagine allo specchio.

Ciò che realmente fa uno specchio è invertire il verso di qualcosa che punta verso di lui. Vediamo in Fig. 5 una freccia che punta verso lo specchio. La sua immagine, vista da O, cambia il verso alla freccia, ossia la freccia viene ribaltata.

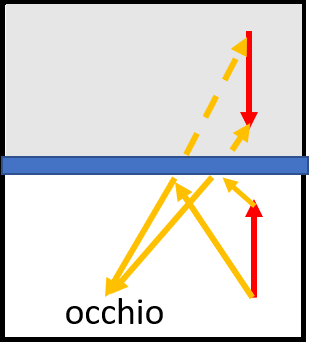
No, non vi è nessuna inversione, ma solo una nostra conclusione del tutto artificiale, dovuta al fatto che non siamo abituati a vivere nel mondo delle immagini...

La grandezza e la lontananza dallo specchio

Capito come funziona lo specchio ci chiediamo due cose: (a) quanto deve essere alto lo specchio per riuscire a vederci completamente riflessi? (b) a che distanza dallo specchio dobbiamo stare per riuscire nella operazione precedente?

Mettiamoci davanti allo specchio a una certa distanza da lui. Per calcolare le dimensioni minime atte a contenerci completamente nell'immagine speculare non dobbiamo fare altro che tracciare i raggi luminosi che partono dal piede e dalla cima della testa e che, una volta riflessi, raggiungono il nostro occhio. Il semplice procedimento lo vediamo in Fig. 6, a sinistra.

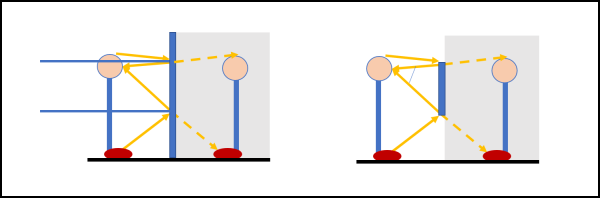
Guardiamo bene dove i raggi incidenti toccano lo specchio e concludiamo che basta uno specchio ben più piccolo delle nostre dimensioni. Tenendo conto che l'angolo di incidenza è uguale all'angolo di riflessione, lo specchio ha un'altezza che è la metà esatta della nostra. La posizione migliore per piazzarlo nel muro è quella in cui il bordo superiore sia a metà strada tra il nostro occhio e la cima della testa (Fig. 6, a destra).

Quanto trovato sembra indicare che l'immagine sia solo la metà della nostra effettiva altezza. In realtà questo è vero, ma l'immagine virtuale che noi vediamo si trova a una distanza dallo specchio che è uguale alla nostra  per cui l'immagine finale ha la nostra stessa altezza.

Ancora più paradossale è, però, la risposta a quanto chiesto dalla domanda (b): la distanza non ha nessuna importanza... il risultato è sempre lo stesso! Basta guardare la Fig. 7 e confrontarla con la Fig. 6 (a destra) per convincersene.

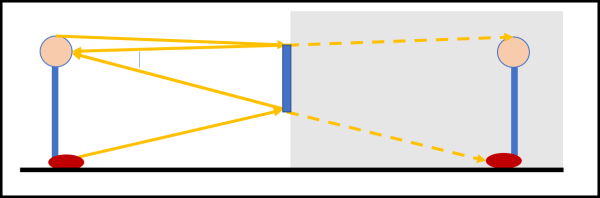
Ciò che cambia non è l'altezza dell'immagine (e nemmeno la nostra) ma le dimensioni angolari dell'immagine. Noi e la Luna siamo sempre alti uguali... ma se ci avviciniamo o ci allontaniamo dalla Luna la vediamo con un diametro angolare maggiore o minore.

Una Venere "guardona"

Concludiamo con un famoso dipinto di Velasquez, dal titolo che inganna: Venere allo specchio.

Il titolo farebbe pensare che Venere si stia ammirando allo specchio... ma questo è impossibile, dato che dalla posizione esterna al quadro si vede Venere riflessa. E' quindi ovvio che Venere non può guardare se stessa, ma guarda, invece, il vigoroso ragazzo disegnato di spalle, ossia colui che guarda il quadro!

A causa della reciprocità della riflessione se qualcuno vede l'immagine di Venere nello specchio, lei deve per forza vedere l'immagine di chi la guarda. La Fig. 8 illustra ancora meglio la situazione.

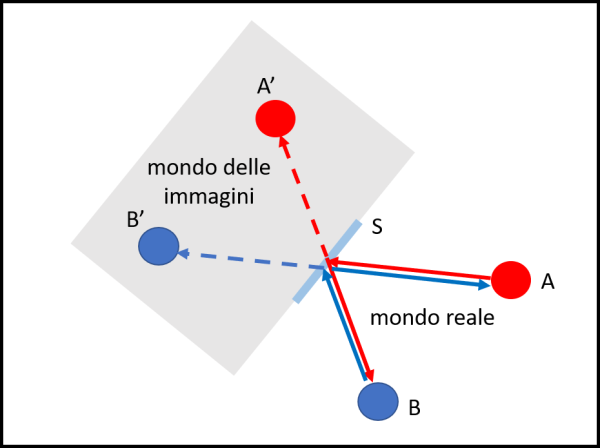
A vede L'immagine di B riflessa nello specchio (raggio blu). B vede, invece, l'immagine di A (raggio rosso). A riesce comunque a vedere B anche direttamente e viceversa. Ma... l'immagine di A vede anch'essa l'immagine di B? Questo è un mistero che non potremo mai risolvere a meno di non vivere realmente nel mondo delle immagini. A questo riguardo vi consiglio di (ri)leggere l'ultimo racconto (Lo Specchio) di questo vecchio articolo .

Non c'è niente da fare, il mondo delle immagini è proprio un mondo fantastico, quasi come quello di Alice!