Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

I vari passaggi che troveremo non sono assolutamente complicati, ma sono un ottimo esercizio di meccanica e di matematica. Non spaventatevi delle formule (in fondo sono solo frasi dette in una lingua meno conosciuta dell’italiano) e cerchiamo di andare avanti con molta calma, spiegando debitamente tutti i passaggi (al limite chiedete aggiunte e/o ripetizioni).

Si potrebbero scrivere libri interi su questo argomento (ed è anche stato fatto), ma noi cercheremo di estrarre i risultati fondamentali, quelli che meglio caratterizzano il moto di un pianeta.

Già partiremo con un qualcosa che ben raramente si tiene in conto e che si dà sempre per buono: la traiettoria di un pianeta (ellisse o cerchio o quello che sia) giace su un piano. L’istinto farebbe dire: “E’ ovvio!”, ma, prima dell’istinto, la matematica preferisce delle prove più decisive.

Il problema, che parte con la legge di gravitazione universale, è gioco forza un problema nelle tre dimensioni x,y e z. Sarebbe una bella scocciatura dover sempre lavorare nello spazio, sia per le figure relative che per i calcoli decisamente pesanti. Sarebbe molto bello togliersi subito il peso dello stomaco e dimostrare che il moto, qualsiasi esso sia, avviene su un piano. In tal modo, potremmo prendere questo piano come quello di riferimento e limitarci a due sole coordinate x e y.

Un bel vantaggio, ve lo assicuro, oltre al fatto che avremmo già un primo risultato che è nascosto nelle leggi di Keplero: l’orbita di un pianeta attorno al Sole avviene su un piano!

Cominciamo a disegnare la Fig. 1 che ci mostra un vettore nello spazio a tre dimensioni.

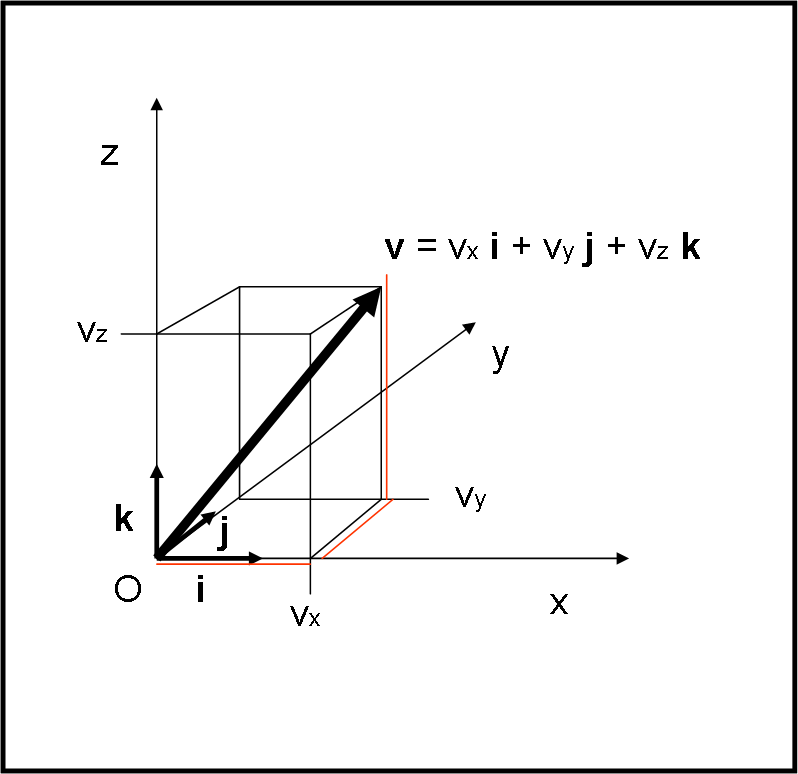
Come ben sappiamo (QUI) esso può essere descritto attraverso i versori i, j, k (relativi a x,y e z) e alle relative componenti. In parole matematiche:

v = v_xi + v_yj + v_z k

Questa è ovviamente una somma vettoriale e si nota facilmente che possiamo sommare prima i primi due vettori e poi, al loro vettore somma, sommare l’ultimo vettore.

Dobbiamo introdurre un primo dato di fatto che non possiamo dimostrare adesso, in quanto vorrebbe dire affrontare la geometria analitica a tre dimensioni (magari prima o poi lo faremo anche) e ci farebbe parlare per mesi… Tuttavia, ciò che stiamo per dire è abbastanza intuitivo.

Ricordiamo qual è l’equazione di una retta nel piano. Noi solitamente l’abbiamo scritta nella forma:

y = mx + n, ossia nella forma y = f(x).

Niente ci vieta, però, di scriverla in modo ancora più generico come:

ax + by + c = 0             …. (1)

Essa corrisponde a F(x,y) = 0 , ma dice esattamente la stessa cosa. Infatti, partendo da (1) si ha:

by = - ax – c

y = - ax/b - c/b = mx + n

Le due espressioni coincidono ponendo m = -a/b  e  n = - c/b.

Avevamo già fatto qualcosa di simile per l’ellisse e per il  cerchio (QUI), scrivendo l’equazione :

x²/a² + y²/b² = 1

Che non è altri che:

b²x² + a²y² = a²b²

ossia

Ax² + By² + F = 0

Essa è un caso particolare di una conica completa:

Ax² + By² + Cxy + Dx + Ey  + F = 0

Torniamo, comunque, alla nostra retta nel piano che ha equazione generale:

ax + by + c = 0

Una retta che passa per l’origine deve essere:

ax + by = 0

ossia y = (-a/b)x = mx

Quale sarà l’equazione di un piano nello spazio? Credetemi sulla parola:

ax + by + cz + d = 0

Questa funzione F(x,y,z) = 0 contiene tutti i punti che stanno su un piano comunque orientato nello spazio.

Se il piano passa per l’origine deve essere:

ax + by + cz = 0   (per O(0,0,0) si ha proprio 0)

in modo analogo alla retta.

E si apre un nuovo mondo che sicuramente vorrei affrontare, prima o poi… Sapete qual è l’equazione di una retta nello spazio? Estremamente complicata, ma anche ovvia: l’intersezione tra due piani non paralleli tra loro, ossia, il sistema:

ax + by + cz + d = 0

a’x + b’y + c’z + d’ = 0

Infatti, due piani non paralleli si tagliano secondo una retta e quindi i punti della retta intersezione devono soddisfare entrambe le equazioni dei due piani. Fermiamoci qui, se no cominceremmo a volare nelle tre dimensioni…

Prendiamo per buono perciò che l’equazione di un piano che passa per l’origine deve essere del tipo:

ax + by + cz = 0         …. (2)

Teniamola da parte, ricordandocela molto bene…

A questo punto, poniamo l’origine degli assi cartesiani in un punto qualsiasi O. Il Sole avrà coordinate x₀, y₀, z₀ e il pianeta P coordinate x, y, z. L’importante è che il baricentro del sistema Sole-Pianeta si muova rispetto a questi assi di moto rettilineo uniforme, in modo che non vi siano accelerazioni tra i due sistemi: l'importante e che il sistema Sole-Terra subisca solo le accelerazioni reciproche, ma non dipendenti dal moto del baricentro rispetto a un sistema esterno.... Stiamo facendo i raffinati, evitando di metterci direttamente nel Sole, ma c’è una ragione di generalità, che non può essere trascurata.  Il succo è che alla fine, facendo le differenze delle coordinate della posizione del pianeta e di quella del Sole, otterremo comunque le loro posizioni relative. Consideriamo la Fig. 2, in cui, per non complicare troppo la situazione, abbiamo solo disegnato il piano (x,y).

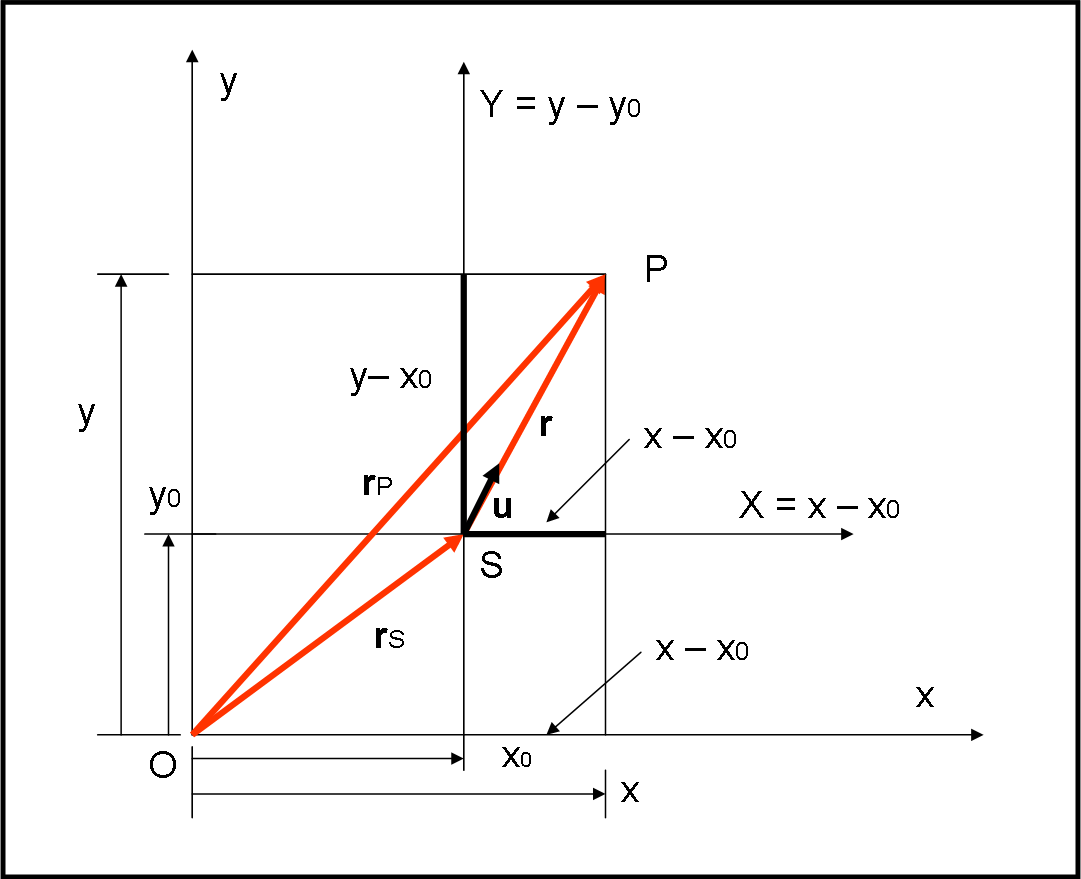
La stessa cosa vale, comunque, estendendo la figura alle tre dimensioni, ossia a ciò che abbiamo visto nella Fig. 1. Potremmo anche disegnare tre figure, ognuna per uno dei tre piani (x,y), (x,z) e (y,z), ma basta e avanza vedere come si opera in un solo piano. Le formule dovranno ripetere pari pari ciò che troviamo nel piano (x,y), cambiando le coordinate in modo corrispondente.

Cosa ci dice Newton? Abbiamo una massa M (Sole) e una massa più piccola m (pianeta) che vengono attratte reciprocamente dalla legge di gravitazione universale che vale, in valore assoluto:

F = G Mm/r²

Dove r è la distanza SP. Una formula che è bene trasformare in forma vettoriale per poi calcolarne le componenti secondo gli assi.

A noi, infatti, interessa affrontare il problema nelle tre dimensioni e dobbiamo fare intervenire  le componenti dei vettori. Facciamo in fretta a mettere le cose a posto. r è ovviamente la congiungente S con P, ossia indica la posizione di P rispetto a S. In altre parole, possiamo esprimere r come vettore, utilizzando il suo modulo r e il versore unitario u lungo la direzione SP:

r = ru

 Moltiplicando il numeratore e il denominatore per r si ottiene la formula di Newton vettoriale:

F = GMmru/r³ = GMmr/r³

Non arrabbiatevi per questo passaggio che sembrerebbe inutile… ma per correttezza dobbiamo trovare le componenti del vettore e non lavorare solo con il modulo della forza.  Sono apparenti piccolezze, ma la Meccanica Celeste è severissima!

Tuttavia, vale anche, per il secondo principio della dinamica, F = ma. Il pianeta è attratto dal Sole con un’accelerazione a_P, mentre il Sole è attratto dal pianeta con accelerazione a_S

Otteniamo:

ma_P = - GMmr/r³

ma anche

Ma_S = GMmr/r³

a_P e a_S sono anche le derivate seconde della posizione di S e di P rispetto al tempo, nel sistema di origine O. Esse non sono certo uguali dato che una è quella che agisce su un corpo di massa m e l’altra su un corpo di massa M; è uguale invece il loro prodotto per la relativa massa, dato che non è altro che la legge di gravitazione.

Si ha, per il pianeta:

m d²r_P/dt² = - GMmr/r³

Il segno meno deriva dal fatto che r va dal Sole verso il pianeta, mentre r_P va in verso opposto.

Notate come abbiamo già introdotto un’equazione differenziale vettoriale? Prima o poi dovremo affrontarle di punta.

Per adesso consideriamo le tre componenti rispetto agli assi x, y e z.

md²x/dt² = - GMm(x - x₀)/r³

md²y/dt² = - GMm(y - y₀)/r³                …. (3)

md₂z/dt² = - GMm(z - z₀)/r³

Mentre per il Sole, abbiamo =

M d²r_S/dt² = GMmr/r³

ossia:

M d²x₀/dt² =  GMm(x - x₀)/r³

M d²y₀/dt² =  GMm(y - y₀)/r³                 …. (4)

M d²z₀/dt² =  GMm(z - z₀)/r³

Il segno vale adesso “più” dato che i vettori sono concordi

Per non riempire di formule l’articolo, svolgiamo il calcolo solo per la x. Una cosa del tutto analoga si ottiene anche per la y e la z.

Consideriamo la prima delle (3) e dividiamola per m. Abbiamo:

d²x/dt² = - GMm(x - x₀)/mr³ = - GM(x - x₀)/r³            …. (5)

Prendiamo la prima delle (4) e dividiamola per M. Otteniamo:

d²x₀/dt² =  Gm(x - x₀)/r³            …. (6)

Sottraiamo la (6) dalla (5) e abbiamo:

d²x/dt² - d²x₀/dt² = - GM(x - x₀)/r³ - Gm(x - x₀)/r³

d²x/dt² - d²x₀/dt² = - G(M + m)(x - x₀)/r³          …. (7)

Facciamo qualche semplificazione.

Chiamiamo x – x₀ = X    (vedi Fig. 2)

Ricordando che la somma delle derivate è uguale alla derivata della somma, si ha anche:

d²x/dt² - d²x₀/dt² = d²(x – x₀)/dt² = d²X/dt²

Poniamo, inoltre, per semplicità e dato che è una costante per il sistema:

μ = G(M + m)

La (7) diventa:

d²X/dt² = - μX/r³              …. (8)

Agendo in modo analogo per la y e la z, otteniamo:

d²X/dt² = - μX/r³

d²Y/dt² = - μY/r³             …. (9)

d²Z/dt² = - μZ/r³

O, ancora:

d²X/dt² + μX/r³ = 0

d²Y/dt² + μY/r³ = 0          …. (10)

d²Z/dt² + μZ/r³ = 0

Le (10) sono le equazioni (differenziali) del moto del pianeta rispetto al Sole. Pasticciamole ancora un po’…

Moltiplichiamo la seconda per Z e l’ultima per Y e poi sottraiamo membro a membro:

Z d²Y/dt² + ZμY/r³ - Yd²Z/dt² - YμZ/r³ = 0

Z d²Y/dt²  - Yd²Z/dt² = 0              …. (11)

Moltiplichiamo la terza per X e la prima per Z e poi sottraiamo:

Xd²Z/dt² + XμZ/r³ - Zd²X/dt² - ZμX/r³  = 0

Xd²Z/dt² - Zd²X/dt² = 0               …. (12)

Moltiplichiamo la prima per Y e la seconda per X e poi sottraiamo:

Yd²X/dt² + YμX/r³ - Xd²Y/dt² - XμY/r³ = 0

Yd²X/dt² - Xd²Y/dt²= 0                …. (13)

Consideriamo la (11). Possiamo scriverla:

d(ZdY/dt – YdZ/dt)/dt = 0        …. (14)

Non ci credete? Proviamo a calcolare la derivata…

dZ/dt dY/dt + Zd²Y/dt² – dY/dt dZ/dt – Yd²Z/dt² = Zd²Y/dt² - Yd²Z/dt²

Come volevasi dimostrare…

Ma se vale la (14) vuol dire che

Z dY/dt -Y dZ/dt = L = costante       …. (15)

La stessa cosa capita per la (12) e la (13) che diventano:

XdZ/dt - ZdX/dt = N = costante        …. (16)

YdX/dt - XdY/dt = Q = costante        …. (17)

Ancora un piccolo sforzo… Moltiplichiamo la (15) per X, la (16) per Y e la (17) per Z e poi sommiamole:

XZ dY/dt - XY dZ/dt + YXdZ/dt - YZdX/dt + ZYdX/dt  - ZXdY/dt = LX + NY + QZ

0 = LX + NY + QZ

In conclusione:

LX + NY + QZ = 0

Ma questa è l’equazione di un piano che passa per l’origine degli assi, cioè per il Sole.  Il che vuol dire che il moto di un corpo (pianeta) soggetto all’attrazione gravitazionale di un altro corpo (Sole) avviene in un piano che passa per il corpo centrale (Sole).

Leggete questo articolo attentamente. Sembra dire delle cose ovvie e invece è di fondamentale importanza, dato che dimostra che le orbite planetarie giacciono su un piano che contiene il Sole. Pensate alla nostra eclittica.

E’ difficile trovare questa dimostrazione, di estrema eleganza stilistica, non solo sul web, ma anche in molti libri. La mia versione, leggermente modificata per essere alla portata di tutti coloro che non si spaventano di qualche passaggio algebrico,  è merito indiscusso del testo di Meccanica Celeste in cui ho studiato tanti anni fa, scritto nel 1953, da quel grande astronomo che è stato Williams M. Smart.

Calma e sangue freddo…

Con uno sforzo non molto maggiore, possiamo arrivare alla descrizione della traiettoria di un pianeta, con il vantaggio non certo trascurabile di potere, finalmente, lavorare su un piano!