Categorie: Relatività
Tags: applicazione della RG buchi neri di Kerr cilindro rotante cono di luce curvatura spaziotempo relatività generale verso la RG viaggi nel tempo
Scritto da: Vincenzo Zappalà
Commenti:4
Viaggiare nel tempo? Basta un cilindro … **
Mentre, piano piano e con molta attenzione, cerco di unire tutti i pezzi della Relatività Generale (in fondo, ha fatto così lo stesso Einstein), vediamo di divertirci con qualche effetto particolare della sbalorditiva formula e delle equazioni che comporta. Non tutte sono state sicuramente risolte e la RG può ancora regalarci scoperte inattese (o quasi). Perché non tornare nel 2016 o anche prima? Viaggiare nel tempo potrebbe aver bisogno solo di un cilindro…
Torniamo solo brevemente alla Relatività Ristretta e alle possibili traiettorie degli oggetti in movimento. In un dato sistema di riferimento si disegna facilmente il cono di luce e si divide il piano di Minkowski in una zona tipo-tempo e in una zona tipo-spazio. Esse sono separate dalle linee descritte dalla luce (tipo-luce). Sappiamo benissimo che il futuro e il passato possono svolgersi solo e soltanto nelle zone tipo-tempo, dove è possibile muoversi senza superare la velocità della luce (gli eventi sono causali). Nella zona tipo-spazio non ci si può muovere dato che si supererebbe la velocità della luce.
Ciò, però, non vuol dire che non si possano effettuare moti accelerati, ossia curvilinei, del tipo di quello descritto (A) in Fig. 1.
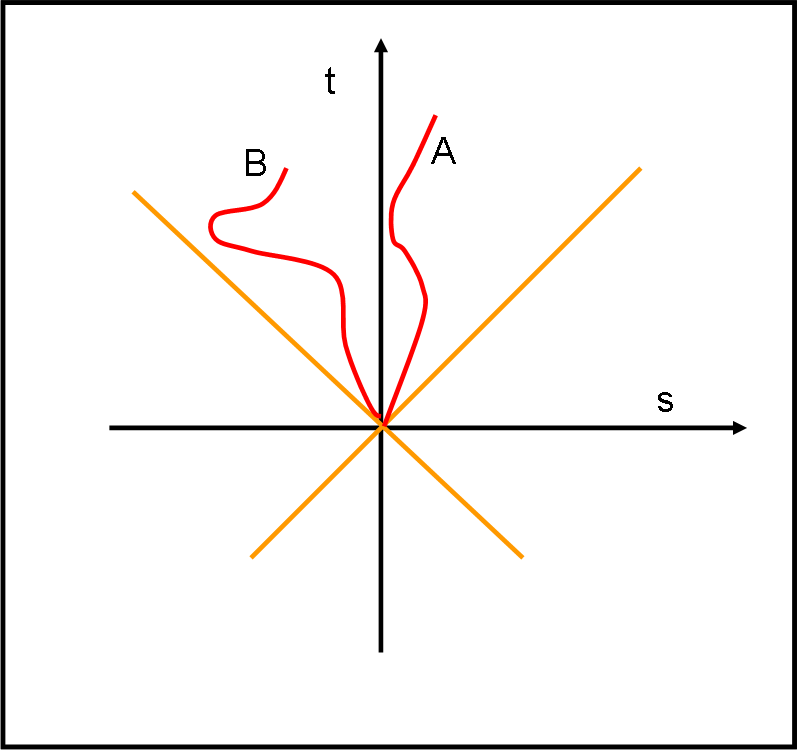
L’importante è che non si raggiungano mai velocità istantanee superiori a quella della luce. Ben diverso sarebbe un moto come quello della curva B. In vari punti di questa traiettoria la velocità supera quella della luce (quelli in cui la tangente alla curva ha un’inclinazione minore di 45° rispetto all’asse delle ascisse) e porterebbe all’assurdo di muoversi nella zona tipo-spazio. Per una “rinfrescata” potete andare QUI.
Fin qui siamo vincolati dalle “leggi” della RR.
Le cose cambiano notevolmente nella RG, dove la presenza di una massa deforma lo spaziotempo. In particolare non dimentichiamo che anche la luce, come tutti gli oggetti solidi, è costretta a “cadere” verso una massa che determina la curvatura dello spaziotempo (lo abbiamo spiegato QUI). Ne segue che, nel nostro piano di Minkowski, il cono di luce dell’oggetto in movimento non può che subire una deformazione corrispondente. Se la luce è costretta a curvare, come conseguenza deve curvare il cono di luce che è proprio delimitato dalle traiettorie della luce. Esso viene piegato verso la massa che introduce il campo gravitazionale (chiamiamolo ancora così).
Questo effetto porta con sé la curvatura dell’asse dei tempi (o viceversa) e tante altre belle cose che abbiamo già introdotto per giungere all’orizzonte degli eventi di un buco nero (il cono di luce è completamente dentro l’orizzonte e la luce non può più uscirne). Tuttavia, noi tralasciamo questa situazione limite e pensiamo solo allo spostamento dell’intero cono di luce. Se andassimo nei dettagli si vedrebbe che il cono di luce non solo si piega, ma si restringe, proprio a causa della differente “caduta” della luce verso la massa. Tuttavia, consideriamo, per ora almeno, solo e soltanto un “tilt” dell’intero cono, come mostrato in Fig. 2.
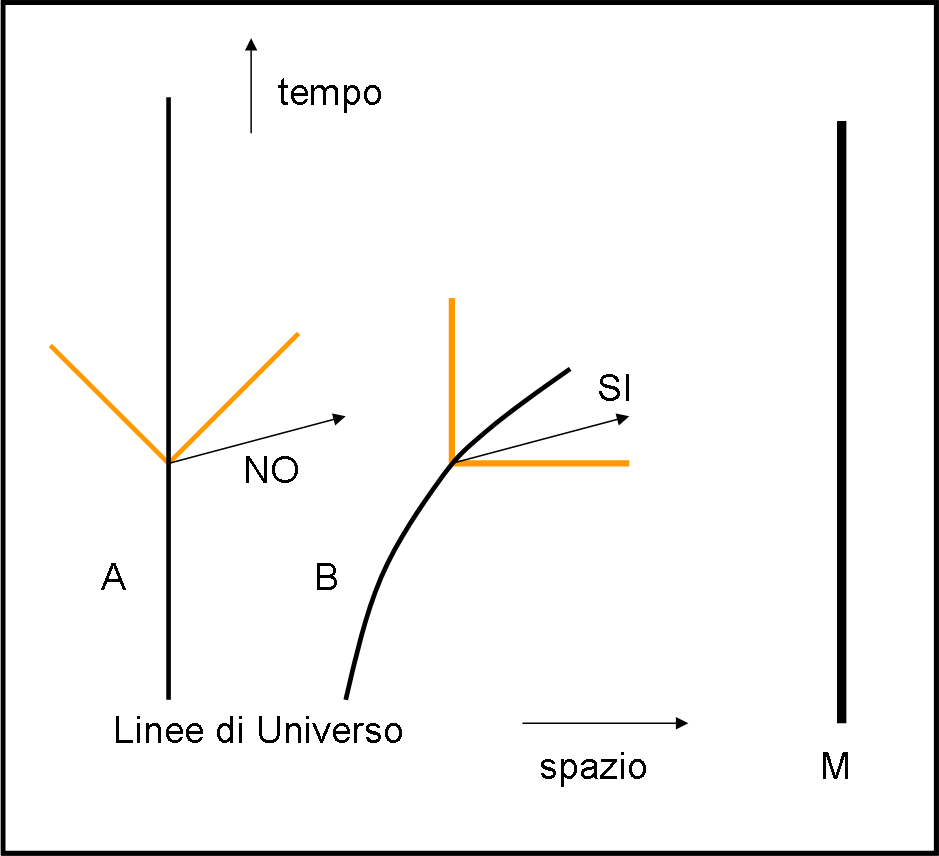
Proprio la Fig. 2 ci mostra un caso limite, quello in cui la luce inviata da B giungerà in A solo in un tempo infinito. Detto in altre parole stiamo realizzano uno strano risultato: la parte del cono di luce causale (tipo-tempo) di un certo oggetto si sovrappone alla parte non causale (tipo-spazio) di chi sta fermo. In parole un po’ rozze, ciò che per qualcuno non può essere raggiunto, se non attraverso velocità superiori a quella della luce, diventa del tutto possibile (causale) per un altro oggetto influenzato pesantemente da un campo gravitazionale. Per l’oggetto che cade verso la massa M è cambiato lo spaziotempo e tutto sembra del tutto normale, ma non per il sistema inerziale
Da un punto di vista teorico potremmo anche ipotizzare una traiettoria come quella di Fig. 3. in cui si nota benissimo come non solo si invada la zona tipo-spazio, ma si vada verso il PASSATO. Ovviamente, la figura è attraente, ma sembrerebbe impossibile, da un punto di vista fisico, potere deformare uno spazio in modo da far girare come un “matto” il cono di luce. Dove starebbe la massa? E altri problemi simili…
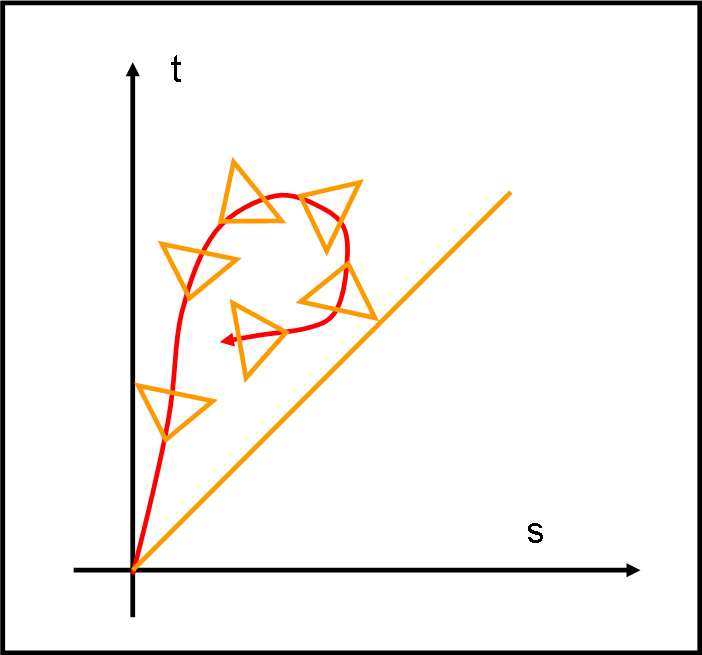
A questo punto torniamo un attimo indietro e riprendiamo in mano la nostra famosa “piastra” gravitazionale (QUI) che faceva girare più lentamente gli orologi e accorciare i righelli. O, se preferite, andiamo a trovare la nostra simpatica ISALBA (QUI). Sappiamo che tutto ciò capita in quanto la “piastra” non è altro che la massa che introduce la gravità come curvatura spaziotemporale.
Tuttavia, dobbiamo prendere atto che tutti quei bei giochini, fatti con la superficie sferica e con certi orologi, Einstein li ha aggiunti in un secondo tempo. Lui aveva "dimostrato", in modo molto controverso, che la rapida rotazione di una massa (che potrebbe anche tendere a zero) determina una curvatura dello spazio tempo attorno a lei, in modo analogo a quanto ottenuto con una piastra.
Consideriamo un disco circolare fermo. Prendiamo i nostri righelli (magari potrebbe farlo ISALBA) e li poggiamo lungo la circonferenza. Ce ne vogliono un certo numero N per coprirla completamente e perfettamente. ISALBA fa la stessa cosa per il diametro e ce ne vogliono M.
A questo punto mettiamo in rapida rotazione UNIFORME il disco con i suoi righelli. Chi ruota con il disco non si accorge di niente: per lui i righelli sono sempre gli stessi. Chi, invece, vede la faccenda dall’esterno, si accorge che ogni righello, la cui velocità istantanea è costante, deve subire una contrazione nel verso del moto. I righelli cambiano lunghezza e si accorciano. Per coprire la circonferenza ne occorrono molti di più di N. D’altra parte, però, i righelli che coprono il diametro sono situati in modo perpendicolare alla direzione del moto e quindi non subiscono variazione alcuna. Conclusione: per qualsiasi osservatore esterno vi è una discordanza tra la circonferenza misurata direttamente e quella misurata attraverso il diametro. Non confondiamo, comunque, questo esperimento con quello "reale" dell'abitante in una superficie curva. In quel caso era proprio l'abitante che si rendeva conto di essere in uno spazio curvo. In questo caso, invece, sarebbe solo l'osservatore esterno.
Einstein concluse che la rotazione di un disco creava uno spazio non euclideo. Non solo l’accelerazione legata alla gravità deformava lo spaziotempo, ma anche l’accelerazione che derivava da una rotazione (accelerazione centripeta, in poche parole). Questo tipo di esperimento mentale è stato giudicato non plausibile dallo stesso Einstein (una specie di paradosso risolto in vari modi), ma gli è stato fondamentale per entrare a fondo nella problematica dello spazio non euclideo. Un errore estremamente utile.
Tuttavia, una soluzione delle sue equazioni ha poi mostrato che lo spaziotempo viene veramente influenzato dalla rotazione velocissima di una massa, come se venisse trascinato insieme a lei. I buchi neri di Kerr (QUI) ne danno conferma.
Questo lungo preambolo è stato inserito per non mischiare i due effetti (come a volte ho letto…): una cosa è la rotazione di un disco e l’ipotetica creazione di uno spazio non euclideo (esperimento mentale di Einstein) e un’altra è la reale deformazione spaziotemporale dovuta all’effetto di trascinamento dovuto alla massa che ruota (soluzione delle equazioni di Einstein)
Arriviamo così al cilindro rotante di Frank Tipler (1974) e alla relativa macchina del tempo.
Invece di un disco, utilizziamo un cilindro rotante ad altissima velocità con una massa di circa dieci volte quella del Sole. La rapida rotazione evita il collasso della struttura, oltre che deformare lo spaziotempo secondo le regole della RG.
Consideriamo la Fig. 4, dove l’asse del cilindro è il suo asse del tempo.
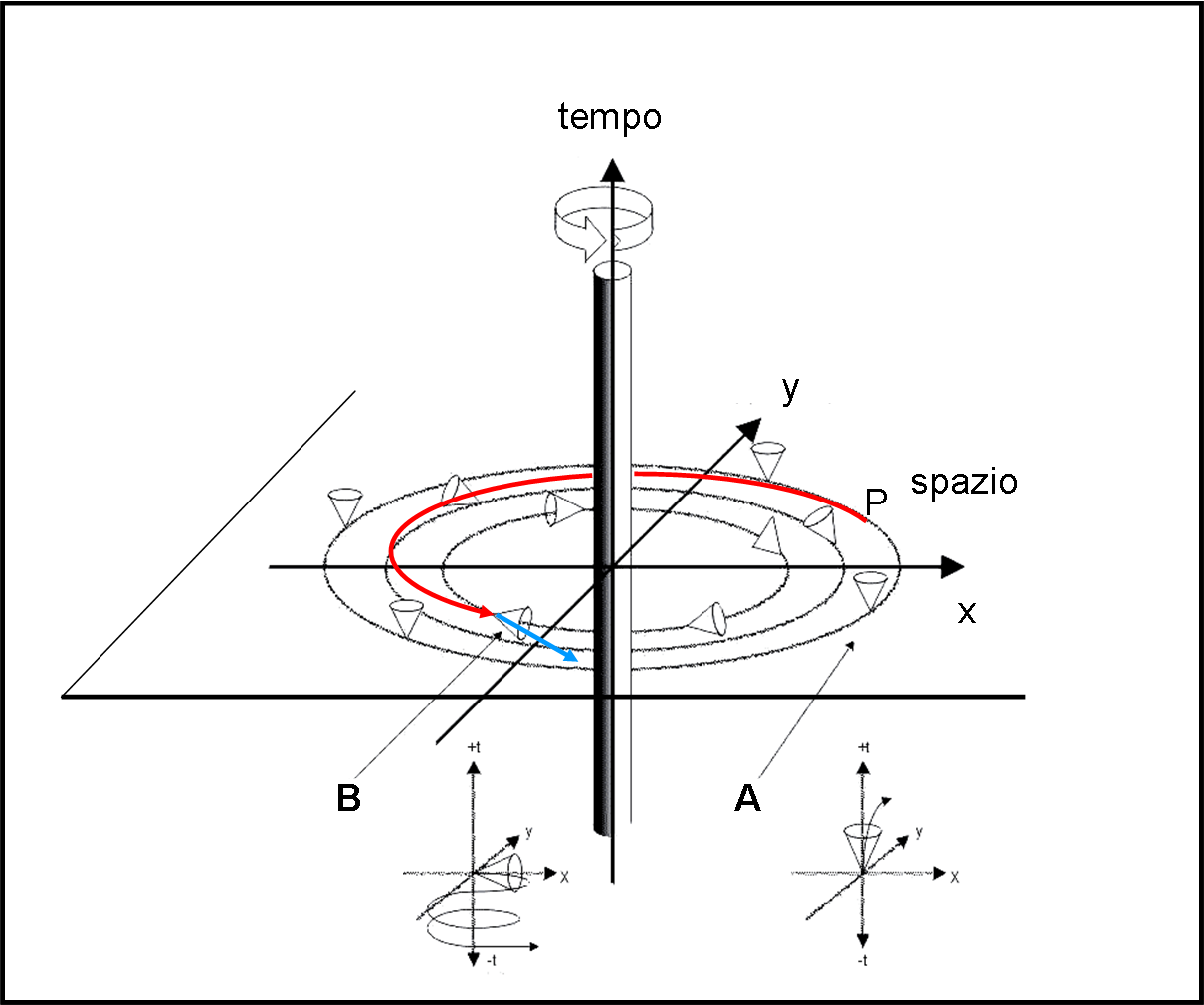
Il viaggiatore P spiraleggia verso il cilindro (curva rossa) nello spazio definito da x e y. A mano a mano che si avvicina al cilindro rotante il cono di luce si piega sempre di più verso di lui fino a inclinarsi di oltre 45°, come in B, dove l’angolo è di 90°. A questo punto sono possibili traiettorie a velocità minori di quelle della luce, tali che il viaggiatore possa tranquillamente tornare indietro (linea azzurra) rispetto al tempo originario (quando era in A), dato che il suo asse del tempo è diventato x.
In parole povere, il viaggiatore si avvicina al cilindro e naviga secondo una traiettoria elicoidale, portandosi verso la parte negativa del tempo pur muovendosi secondo traiettorie con velocità inferiori a quella della luce. Notiamo la completa coerenza della situazione: il viaggiatore resta sempre all’interno del suo cono di luce locale futuro. Giunto a un certo tempo passato, basta che si allontani lentamente dal cilindro e esce dall’elica vivendo una vita normale (il cono di luce riprende la direzione iniziale). Tutto ciò nel pieno rispetto delle leggi della matematica e della fisica.
In realtà ciò che è descritto potrebbe anche avvenire all'interno di un buco nero. Ma, in questo caso, sarebbe molto difficile uscirne e -soprattutto- sani e salvi!
No, non illudiamoci più di tanto… La costruzione del cilindro non è certo cosa semplice e le sue caratteristiche sembrano portare a situazioni assurde come spiegato anche da Hawking. Tuttavia, la porta non è ancora del tutto chiusa, soprattutto facendo giocare in qualche modo la fisica quantistica. Chissà… le equazioni di Einstein nascondono ancora molti misteri e non tutte sono state completamente risolte.
Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.
QUI trovate l'approfondimento dedicato alla Relatività Generale
NEWS del 26/9/2020: Uno studio apre le porte alla possibilità teorica di viaggi nel tempo senza paradossi "fisici".






4 commenti
Chiaro e allo stesso tempo sconcertante....Tanto di cappello...(a cilindro)
Beh ormai con Enzo la chiarezza è evidente e lo sconcerto affascinante e obbligatorio. Pian piano andiamo a capire quanto è particolare, magico e bello l'Universo e tutto ciò che ci sta dentro , compreso noi. Tutto correlato, tutto Uno.
aimé ho capito poco...HELP ME ENZO
Beh sì, Gianluca, non è molto semplice. E' necessario avere basi ben chiare di RR e di concetto di cono di luce e della sua deformazione nei pressi di un massa. In pratica si otterrebbero le stesse deformazioni di un buco nero (dal quale non si potrebbe mai uscire) con un cilindro rotante, sfruttando il fatto che lo spaziotempo si deve deformare dato che sulla circonferenza i righelli (posti nel verso del moto) devono accorciarsi , mentre quelli in senso perpendicolare non lo fanno (come insegna la RR) . Abbiamo così un cono di luce, che indica il futuro del viaggiatore che si piega fino a permettergli di tornare indietro nel tempo. Non essendo dentro un buco nero, il viaggiatore può sempre uscire dalla "giostra" del tempo al momento voluto.
Insomma, Einstein considerava spesso alcune sue idee come errori, salvo poi essere riprese da altri e utilizzati anche se -per adesso- solo mentalmente. La famosa costante delle sue equazioni è servita per introdurre l'energia oscura... Non poteva nemmeno permettersi di sbagliare!