Categorie: Relatività
Tags: curvatura densità massa relatività generale spaziotempo verso la RG
Scritto da: Vincenzo Zappalà
Commenti:11
Fermiamoci a riflettere: la relatività generale deve essere di TUTTI *
Per una trattazione completa della Relatività Generale, si consiglia la lettura del relativo APPROFONDIMENTO, del quale fa parte anche il presente articolo
Un momento di riflessione nella trattazione della Relatività Generale. Potremmo considerarlo un’introduzione, ma anche un riassunto conclusivo. Tutto sta nel come vogliamo entrare nel suo Universo meraviglioso. In un modo o nell’altro, è fondamentale che TUTTI possano essere in grado di avvicinarsi alla più strabiliante teoria del macrocosmo.
Potremmo andare avanti nella descrizione della relatività generale (RG) utilizzando qualche formula in più (senza esagerare, ovviamente) e arrivare abbastanza velocemente (non dimostrando proprio tutto) a esprimere in linguaggio matematico (e fisico) la teoria che la riassume. In fondo, i punti essenziali li abbiamo già toccati e spero, anche, in modo abbastanza comprensibile.
D’altra parte, la RG spiega il tutto (o quasi) e non sarebbe giusto se fosse a conoscenza solo di pochi eletti. Se spiega il tutto (o quasi) deve essere compresa da TUTTI (o quasi).
Tuttavia, dato che non possiamo svilire più di tanto il lavoro di Albert (anni e anni di sofferenza, di delusione e di lampi di genio apparentemente assurdi), è giusto cercare di capire meglio la situazione a cui siamo arrivati e nel contempo renderci conto delle difficoltà potenziali da superare per sostituire alla semplice legge di Newton un qualcosa di ben più generale che riesca a non fermarsi di fronte a corpi celesti con proprietà fisiche ben diverse da quelle del nostro piccolo mondo quotidiano. Lo faremo, ma cercando di portare più avanti possibile, insieme a noi, anche i meno preparati e i più piccoli.
Speriamo anche che questi tentativi continui servano agli insegnati e li stimolino a riflettere sulla RR e sulla RG, soprattutto. La più grande rivoluzione scientifica ha ormai cent’anni, eppure nelle scuole non si insegna. E non si dica: è cosa per pochi eletti. Assolutamente no: tutto ciò che spiega la realtà deve essere alla portata di tutti, dato che tutti facciamo parte della realtà. Basta studiare, capire, smussare gli angoli e divulgare. Buona scuola vuole anche dire buoni insegnanti!
Iniziamo con qualche riflessione di carattere generale…
Ricordiamo che Einstein non aveva la possibilità di ottenere osservazioni sui giganti cosmici e quindi la parte più essenziale della sua teoria era nascosta completamente (o quasi) dalla limitatezza delle osservazioni terrestri. Non per niente, furono altri scienziati a dedurne le infinite applicazioni che ancora oggi portano a continue conferme.
E’questa la grandezza suprema dell’intera faccenda. Poter lavorare solo su un paio di numeri interi e piccoli e riuscire a ragionare in termini giganteschi che solo i computer possono oggi regalarci. Facciamo un esempio… Il calcolo di un’orbita era già possibile ai tempi di Keplero, ma nessuno poteva certo pensare di arrivare a calcolare il viaggio di una navicella spaziale sotto l’effetto delle innumerevoli perturbazioni planetarie. C’era la potenzialità, ma per riuscire a farlo bisognava ancora scrivere tutta la meccanica celeste. I pianeti e i satelliti erano lì, con i loro movimenti, con una loro storia passata e futura. Tuttavia, la meccanica celeste doveva fermarsi e attendere i computer per prevedere o ricordare gli eventi dinamici accaduti nel nostro sistema planetario su tempi scala delle decine di milioni di anni.
Einstein ha fatto qualcosa di molto diverso. E’ come se fosse stato un Keplero in grado di scrivere una formula senza confini, né verso l’infinitamente piccolo (magari, prima o poi, con l’aiuto della meccanica quantistica arriverà al “nucleo” di tutto), né verso l’infinitamente grande. Bastava fare i calcoli e aspettare che l’uomo fosse in grado di misurarli nella realtà dell’Universo. Esattamente il contrario di quanto normalmente succede (o dovrebbe succedere) nella Scienza.
Galileo ne sarebbe fiero e un po’ imbarazzato. E’ vero che il suo illustre collega si basa, in fondo, sull’osservazione della realtà, ma i suoi voli di fantasia e di estrapolazione vanno ben oltre il suo metodo scientifico. Anzi, sembrano di una libertà mentale troppo rischiosa e fondata solo su idee e non fatti.
Forse è stato proprio Einstein a lanciare la moda delle teorie più astruse sull’Universo, la sua nascita e il suo evolversi. L’unica differenza sta nella qualità del cervello e nelle possibilità deduttive. Lui poteva permetterselo perché vedeva dove nessuno riusciva a vedere, inquadrava logicamente ciò che sembrava completamente slegato. Ma, soprattutto, non temeva le prove osservative, anzi le sperava, tanto era la sua fiducia nel quadro che aveva completato. Oggi, le teorie più astruse nascono, il più delle volte, proprio perché sarà probabilmente impossibile verificarle.
Sicuramente (ma non ne sono tanto sicuro) si riuscirà a migliorare la relatività generale e il cammino da percorrere è quello aperto, anzi socchiuso, dalla meccanica quantistica, ma bisognerà aspettare qualcuno che faccia sua la concezione generale di Einstein e che abbia le sue stesse capacità deduttive.
Ecco perché, spesso e volentieri, divento una furia quando sento perfetti ignoranti, senza alcuna base fisica, senza apertura mentale e senza una minima visione generale di quanto sia complessa, armoniosa, poetica, artistica e… semplice la teoria del grande Albert, proporre cambiamenti, sollevare critiche, suggerire teorie che contengono grandezze e particelle che nemmeno sanno cosa siano. Il loro luogo di azione non è l’articolo scientifico pubblicato e libero di essere valutato… no, il loro mondo vuoto e squallido è il “forum”, dove tutti possono dire tutto senza nemmeno pensare a studiare, a riflettere e a rischiare veramente in prima persona.
Ma torniamo a noi e alla nostra teoria che ci sta aprendo le porte delle sue meraviglie. Meraviglie che, purtroppo, saremo solo in grado di osservare da lontano, di apprezzare superficialmente, sapendo che certi segreti ci sono ancora vietati nei loro risvolti più sottili e brillanti. Tuttavia, è già un grande risultato, una grande conquista del pensiero e della conoscenza. Il piacere è comunque assicurato, se tenuto a freno da una sana e indispensabile umiltà scientifica e culturale.
Ho parlato senza freni e senza direzioni prescelte… sono andato dove mi portava il cuore. Adesso, però, è ora di tornare a noi e cercare di capire sempre meglio l’essenza dell’opera d’arte, osservandola nel suo insieme e nelle sue finalità più generali.
La cosa migliore è iniziare da un confronto terra-terra tra ciò che diceva Newton e ciò che dice Einstein, con tutto il più grande rispetto e gratitudine per il suo sconfinato maestro.
Gravità = curvatura spaziotempo
Questa è l’uguaglianza fondamentale, da tradurre in una teoria che cambi completamente la concezione del Cosmo.
Cominciamo dalla descrizione della curvatura. Non è certo cosa semplice. Noi l’abbiamo fatto con una superficie sferica (QUI) e già ci sembra di essere andati lontano, superando non pochi scalini legati alla realtà quotidiana. La curvatura di cui si avrà bisogno, a parte la sua struttura spaziotemporale e non solo spaziale, è decisamente variabile e difficilmente calcolabile (lo vedremo più in là). Tuttavia, può venirci in aiuto, per comprendere almeno le difficoltà intrinseche, fare un confronto con gli effetti derivanti dalla gravità newtoniana. Ciò che si trova nella teoria di Newton deve essere presente anche nella Relatività. Le due cose devono essere del tutto equivalenti! Vogliamo o non vogliamo dimostrare che tutti gli effetti conosciuti da Newton sono dovuti a qualcosa di nettamente diverso, ma che li spieghi perfettamente? E allora affrontiamo gli ostacoli che ci prospetta Newton e trasferiamoli alla curvatura.
Andiamo avanti con i piedi di piombo… E teniamo ben presente che ormai siamo costretti a pensare sempre in termini di spaziotempo, come ci ha dimostrato benissimo quella piastra così strana che deforma lo spaziotempo attorno a lei. Non parliamo più di massa o di densità della materia (cosa, comunque, decisamente migliore), ma pensiamo a un qualche strano macchinario che Einstein ha già preparato adeguatamente attraverso la sua dinamica relativistica. Massa ed energia, ricordate? Anche questo sarà un punto complesso da definire: un marchingegno che sia in grado di deformare lo spaziotempo… e dico poco!
Facciamo, allora un passo indietro per riassumere ciò che abbiamo dimostrato fino ad ora. Non siamo molto lontani dalla fine, se escludiamo la traduzione in linguaggio matematico.
Prepariamo uno schema veramente elementare che ci faccia posare i piedi per terra (anzi librare nello spazio) e capire esattamente con cosa abbiamo a che fare. Può sembrare una pagina di un libro da scuole elementari. Qualcuno, forse, si rifiuterà di leggere, pensando che le sue conoscenze siano ben superiori. Noi, e io per primo, ci troviamo, invece, a nostro agio, dato che di fronte al genio di Newton e di Einstein, non possiamo che sentirci bambini con la bocca semiaperta per lo stupore.
Per rendere il tutto ancora più infantile vorrei introdurre un personaggio che ci aiuterà a capire dove ci stiamo trovando. Forse, ci aiuterà a portarci dietro, nel nostro viaggio, anche i veri bambini. Un personaggio femminile, però. E’ora di non limitarci più a scienziati, ad astronomi, a studiosi in genere. Probabilmente chi farà il passo successivo verso l‘unione totale di mondo relativistico e quantistico sarà una donna, dotata di una fantasia e di una sensibilità sottile che gli uomini non hanno. La chiamiamo ISALBA (l’etimologia del nome non è difficile da comprendere) e ve la presento nella Fig. 1.

Come vediamo, Isalba è munita di un righello e di un orologio, più che sufficienti per insegnarci la strada da seguire. In fondo, li conosciamo già (ricordate la prova di esame di Einstein e Newton QUI fig. 13 e 14?). D’altra parte vogliamo entrare nello spaziotempo e un righello per misurare le distanze e un orologio per misurare il tempo sono sufficienti. Immaginiamo che vi siano un certo numero di Isalbe sparse nel vuoto del Cosmo.
Fermi tutti, sappiamo benissimo che il vuoto non è veramente vuoto, ma per adesso possiamo facilmente soprassedere. Vuoto, vuoto… sembrerebbe qualcosa che non esiste e non può esistere. In realtà, è meglio cambiargli nome e chiamarlo proprio spaziotempo. Lo possiamo anche definire come struttura atta a essere misurata in qualche modo. Se non si misura, lo spazio cessa di esistere e se l’orologio non si muove il tempo non passa.
Questo è il ragionamento di fondo. Lo spaziotempo, quindi, è un qualcosa che ha senso solo se si riesce a misurare attraverso una certa geometria con un numero qualsiasi di dimensioni. Noi viviamo in uno spazio a quattro dimensioni e la sua geometria comprende anche il tempo. E’ ovvio, quindi, che Isalba si sia munita di un righello e di un orologio… senza di loro lo spaziotempo non esisterebbe e lei (come tutti noi) non potrebbe entrarci.
Invece vediamo con piacere che si trova a suo agio e quindi vuol dire che lo spaziotempo esiste ed è, conseguentemente, misurabile (ma vale anche il viceversa).
Le nostre Isalbe, in Fig. 2, si divertono, perciò, a misurare distanze, a segnare intervalli di tempo, a scoprire le dimensioni in cui sono immerse.

Possiamo anche dire, con una certa sicurezza, anche perché siamo in una piccola regione di spaziotempo, che i righelli e gli orologi funzionano perfettamente e vanno in perfetto accordo. Ci lanciamo a dire una parola difficile: lo spazio è euclideo! Sappiamo bene cosa vuol dire, ma è sempre meglio richiamarlo. Esso è misurabile attraverso la geometria euclidea, ossia si può applicare il teorema di Pitagora, le rette parallele non si incontrano mai, la somma degli angoli interni di un triangolo è 180 gradi, ecc., ecc. In ogni modo, le caratteristiche di uno spazio euclideo e di uno spazio curvo le abbiamo analizzate a lungo QUI.
Le nostre simpatiche amiche stanno costruendo lo spaziotempo, proprio perché lo spaziotempo è un qualcosa che serve a dirci dove siamo. Ognuna di esse rappresenta un evento, ossia ha una certa posizione in un certo istante (l’analogo del punto nello spazio a tre dimensioni).
Per non rischiare di creare confusione, diciamo subito che Isalba non si muove rispetto alle altre. Se lo facesse rischierebbe di entrare in crisi profonda: le misure di spazio e tempo cambierebbero e le nostre amiche non andrebbero più d’accordo.
Basterebbe spiegarle che esiste la relatività speciale e loro capirebbero cos’è quella strana apparenza che hanno i righelli e gli orologi se visti da Isalbe diverse, in movimento uniforme una rispetto all’altra. Ma noi queste cose le sappiamo già e sappiamo anche bene come tutto sia perfettamente simmetrico, per cui possiamo, almeno per il momento, escluderle dal nostro discorso. Noi siamo interessati a qualcosa che capiti solo in certe condizioni e che tutti possano vedere e confermare. Qualcosa di “assoluto” (occhio che ciò non è in effetti possibile) e non di soggettivo.
Ed ecco che nel nostro spaziotempo compare un “qualcosa”. Newton la chiama massa, Einstein la definisce in modo più complesso e pensa a lei come a un marchingegno in cui materia ed energia diventino una sola cosa. Per adesso, comunque, non c’interessa più di tanto. Passiamo alla Fig. 3.
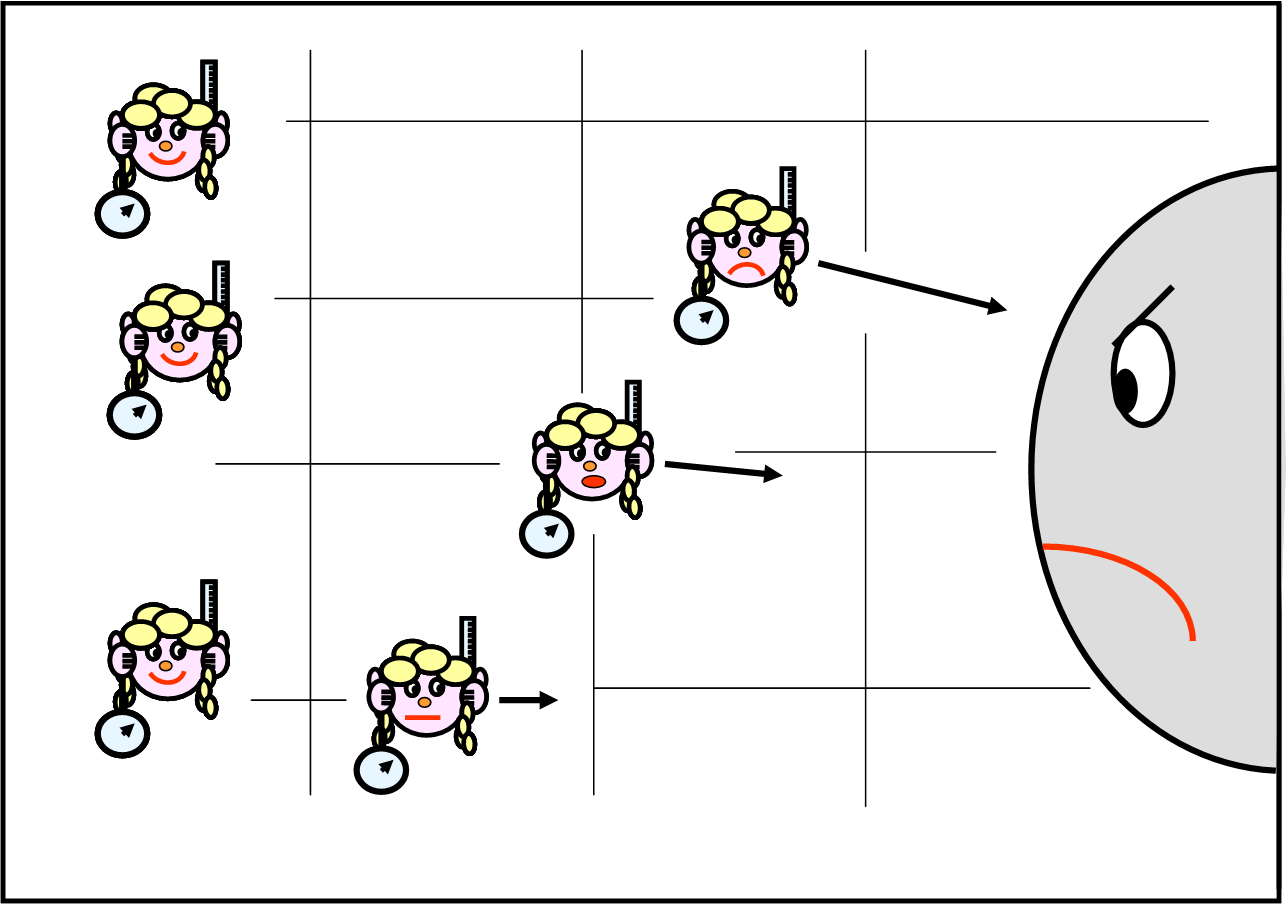
La presenza di questa “massa” (chiamiamola così per semplicità) sta modificando le azioni di Isalba e delle sue compagne, in modo inaspettato. Righelli e orologi funzionano ancora? Sembra di sì, almeno a prima vista. Cosa sta succedendo allora? Bene, le Isalbe più vicine alla massa si sentono trascinate verso di lei in modo violento, mentre quelle più distanti lo fanno in modo meno violento. Chi è ancora più lontana non se ne accorge nemmeno.
Non è difficile disegnare vicino a ogni Isalba una piccola freccia che indichi il loro movimento o, se preferiamo, velocità (variazione dello spazio percorso in funzione del tempo). Ci accorgiamo che questa velocità cambia in modo tale, però, che la sua variazione (accelerazione) rimane costante. Che cos’è che tira verso di sé le Isalbe? Non esiste corda nello spazio (possiamo parlare solo di spazio, essendo nel mondo newtoniano) e la colpa deve essere di quella massa comparsa dal nulla. Essa deve essere capace di spostare le “cose” anche senza toccarle.
Una maga in piena regola, una maga che segue una legge piuttosto semplice: chi è più vicino viene tirato di più. Siamo di fonte a una vera caduta “libera” verso un qualcosa che agisce nello spazio. Lo spazio, allora, non è solo un vuoto che esiste perché è misurabile, ma è un qualcosa che ammette poteri magici che agiscono a distanza. Diamogli un nome: forza o campo o quello che vogliamo. Non si possono toccare, ma esistono e si vedono chiaramente attraverso i loro effetti sulle nostre Isalbe.
Nel frattempo è comparsa un’altra massa, ancora più potente. Per definire cosa sia più massiccio di un’ altro, Isalba ha bisogno di altri strumenti oltre che al righello. Quest’ultimo le può solo dire chi è il più grande, come dimensioni spaziali, ma si rende conto che non basta. A parità di dimensioni una massa è più massa di un’altra… in poche parole, cambia la densità della materia che riempie il volume misurato con il righello. Einstein, frattanto, se la ride… dato che il suo marchingegno si basa essenzialmente sulla densità.
Ma torniamo al mondo newtoniano. Ci siamo accorti che la magia che attira le cose dipende anche dalla massa della cosa che è apparsa dal nulla. Più ne ha e più gli effetti magici sono importanti ed evidenti. Tuttavia, scopriamo anche un’altra cosa fondamentale: le Isalbe cadono tutte con la stessa velocità, se si trovano alla stessa distanza dalla massa, indipendentemente da quanto siano massicce loro stesse.
E qui, forse, Newton avrebbe già dovuto pensare che qualcosa non andava bene nella sua descrizione. Perché mai la massa di chi subiva non contava assolutamente niente nel fenomeno magico? La spiegazione era di comodo: la massa giocava un doppio ruolo, quello di resistere e di cedere alla massa preponderante. In parole più tecniche, la massa m che compare nella legge di gravitazione universale (F = GMm/r2) è la stessa che compare nel secondo principio della dinamica (F = ma).
L’unico problema era che se qualcosa non avesse avuto massa non avrebbe dovuto cadere. Perfetto, almeno fino a che Einstein non è arrivato a cambiare le carte in tavola. Sarebbe stato importante chiedere a una particella piccolissima e mai ferma: il fotone. Lui non ha massa eppure cade come le Isalbe… Ma questo Newton non poteva ancora saperlo.
Attenzione. Sembra che si stia facendo fare a Newton la figura dello sprovveduto. Ci mancherebbe altro (la nostra è solo una favola molto approssimativa): l’uguaglianza tra massa gravitazionale e massa inerziale è un problema ancora al centro di animate discussioni. Einstein non ha fatto altro che … girarci intorno…
Tuttavia, è obbligatoria una considerazione. Einstein non ha, in realtà, sfruttato le osservazioni dell’Universo per mettere in discussione la visione di Newton. Più o meno le conoscenze erano le stesse. La sua teoria, perciò, non nasce da evidenze osservative, ma da una visione mentale diversa. Una visione assurda, strabiliante e rischiosissima per la sua stessa reputazione scientifica.
E’ giunta, finalmente, l’ora di guardare, con più attenzione (Fig. 4), cosa stanno facendo le nostre amiche che stanno cadendo per magia verso la massa. Accidenti, lavorare attorno a un pianeta “piccolo” come la Terra comporta grandi problemi. I righelli e gli orologi sembravano sempre gli stessi e invece…

Einstein vede (anzi, immagina soltanto, ma ha pienamente ragione) che i righelli si accorciano mentre le nostre amiche cadono verso la massa. Non solo, però, anche i loro orologi girano sempre più lentamente (ossia il tempo misurato diminuisce). Quella che sembrava una magia che operasse all’interno dello spazio (e il tempo) sembra essere proprio una modifica dello spaziotempo.
La massa, o chi per lei, deforma la geometria con la quale le nostre amiche erano riuscite a misurare distanze e tempi. Le regole della geometria euclidea non valgono più e bisogna utilizzare quelle “strambe” di una superficie curva (QUI).
Abbiamo già visto come una piastra molto speciale possa riuscire a fare questo (QUI) ed ora Isalba e compagne lo toccano con mano. In realtà chi sta cadendo non se ne può accorgere, dato che per lei nulla cambia. Ma chi sta fuori dalla mischia lo può notare facilmente, dovunque si trovi. Einstein è riuscito a mettersi in quelle condizioni! E’ riuscito a dimostrare una curvatura intrinseca nelle quattro dimensioni senza poter passare in una dimensione superiore. Meraviglioso, meraviglioso!
Ma, allora, tutto può cambiare e diventare addirittura più semplice. Non c’è nessuna forza magica che attira le cose (o almeno non nel senso che Newton aveva pensato), ma è lo spaziotempo deformato che costruisce strade speciali per condurre Isalba e le amiche verso la massa o la piastra o quello che preferite.
Siamo in uno scambio ferroviario, dove ogni linea ferroviaria viene incanalata verso la stazione centrale (la massa). Un binario, però, non cambia a seconda del treno che arriva: la stessa linea verso la stazione può essere seguita da un freccia rossa o da un regionale. In altre parole, è ovvio che la massa di chi cade non conti più! Giunti nella periferia di una grande città (una grande piastra) ogni treno (Isalba) segue la linea più “rapida” per arrivare nella stazione centrale. Il rapida assume però un significato diverso, proprio perché le caratteristiche dello spaziotempo non sono euclidee. Ma ci torneremo presto… Ci basti dire (come già accennato QUI ) che la linea da seguire (la più corta) è quella che corrisponde al tempo più lungo. Nel nostro mondo euclideo la verità è proprio il contrario: la strada più corta è quella che è percorsa nel tempo minore
Questa è la realtà dello spaziotempo. Esso non è una struttura fissa e inamovibile come un teatro in muratura. Esso è un qualcosa che localmente si può sbizzarrire ad assumere “forme” diverse, variabili, curve o quello che preferiamo usare come analogia. Addirittura, tutto l’universo potrebbe risentire di queste variazioni locali… da cui la famosa “forma” dell’Universo (QUI)
Accidenti, ma era così semplice… altro che magia… è solo questione di strade e di ferrovie che permettono gli spostamenti nello spaziotempo. Peccato che nessuna osservazione poteva confermarlo e ci sono voluti anni per dimostrare che la soluzione di Einstein era quella giusta (e quindi niente Nobel per la più straordinaria teoria della Scienza macroscopica). Teoria che giorno dopo giorno ottiene nuove conferme (buchi neri, onde gravitazionali, ecc. ecc.).
La RG è tutta qui. Bisogna solo scrivere una relazione tra curvatura e piastra. E qui le cose si complicano. Einstein ha saputo cercare e capire. La descrizione di una curvatura variabile, a quattro dimensioni, era già stata elaborata. Così come la sua dinamica relativistica era in grado di costruire una piastra capace di deformare lo spaziotempo. Bastava eguagliare due espressioni e tutto si risolveva.
Qualcuno, ogni tanto, dice che Einstein ha approfittato degli studi degli altri (Lorentz, Ricci, ecc.). Sicuramente ha utilizzato qualcosa di conosciuto, studiandolo e capendolo a fondo (e questo la dice lunga sulla sua umiltà culturale), ma ha saputo genialmente adattare qualcosa di puramente teorico a qualcosa di eccezionalmente pratico. E poi, cari amici, legare curvatura con masse ed energia è pur sempre un’idea che poteva venire solo a lui. Eppure era proprio quella giusta.
Tra parentesi, una piccola chicca… Sembrerebbe che Einstein abbia risolto brillantemente il fatto che il fotone cada anch’esso verso la stazione attraverso una rete ferroviaria. Massa o non massa, i binari sono quelli. Tuttavia, a voler essere sinceri, la deformazione dello spaziotempo è pur sempre un qualcosa di “attrattivo” (le masse cadono verso qualcosa) e la massa del treno gioca la sua parte.
Il non avere massa darebbe comunque grossi problemi interpretativi. Ma Einstein ha risolto quasi automaticamente questo “problemino”. Ricordiamo che il fotone non ha massa a riposo, ma ha energia (e qui la MQ si affaccia alla grande) e quantità di moto (deve averla per forza visto che non sta mai fermo!). Tuttavia, la massa non è altro che la quantità di moto divisa per la velocità. E allora, eccoci servita su un piatto d’argento una strana massa relativistica del fotone che lo fa diventare un treno vero e proprio.
Non so ancora fino a che punto proverò a entrare nei tensori e nei risvolti più sottili della formula generale della RG (semplicissima all’aspetto, ma…). Di sicuro analizzeremo meglio che tipo di curvatura abbiamo di fronte avvicinandoci alla piastra. Noi abbiamo sempre parlato di “curvatura” media, ma la curvatura di cui abbiamo bisogno è ben più complessa (non per niente Einstein ha dovuto cercare e ricercare per trovarne una descrizione soddisfacente). Ci limiteremo ad alcuni effetti di curvatura che sono sotto gli occhi di tutti (si fa per dire). Newton non li aveva considerati ma esistevano anche lavorando solo con la sua teoria… D’altra parte la RG deve risolvere tutto ciò che trovava e spiegava Newton: la realtà è quella e una teoria non può mai cambiare la realtà.
Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.
QUI trovate l'approfondimento dedicato alla Relatività Generale






11 commenti
[Su Max Planck] Era una delle persone migliori che io abbia mai conosciuto [...] ma non capiva proprio niente di fisica perché durante l'eclissi del 1919, è rimasto in piedi tutta la notte per vedere se sarebbe stata confermata la curvatura della luce dovuta al campo gravitazione. Se avesse capito davvero [la teoria della relatività], avrebbe fatto come me e sarebbe andato a letto.
Albert Einstein.
A proposito di geni!
grazie Gianni!!!
Dall'art. "Ricordiamo che il fotone non ha massa a riposo, ma ha energia (e qui la MQ si affaccia alla grande) e quantità di moto (deve averla per forza visto che non sta mai fermo!). Tuttavia, la massa non è altro che la quantità di moto divisa per la velocità."
Ma, quindi, anche se in piccolissima parte, il fotone contribuisce anche lui, con la massa relativistica, alla curvatura dello spaziotempo? Ho sempre pensato che il fotone, senza massa, si incurvava in presenza di masse importanti seguendo le linee dello spazio tempo.
Stiamo attenti a non prendere tutte le frasi come se appartenessero al linguaggio della fisica classica. La massa di Einstein solleva ancora profonde discussioni in merito. Molti preferiscono parlare solo di quantità di moto e considerare massa solo quella a riposo. E' la quantità di moto che gioca il ruolo fondamentale e quindi il fotone ce l'ha anche senza avere massa. Con quella frase volevo solo dire che, in fondo, l'introduzione della relazione massa/energia potrebbe anche far pensare a un fotone realmente "attratto" e ricadere nella meccanica newtoniana... Comunque, la sua massa relativistica non può contribuire alla curvatura dello spaziotempo, ma ne è soggiogata.
Grazie per la disponibilità, come sempre
grazie a te Gimar per l'interesse che dimostri e non mollare nel chiedere!!!
È preferibile dire che " il fotone non ha massa" , punto e basta . L'aggiunta "di riposo" per me è fuorviante , innanzitutto perchè il fotone non riposa mai, non è mai possibile definire un sistema di quiete del fotone , non gli si può attaccare in testa un riferimento ch si muova con lui , perchè in tale riferimento il fotone sarebbe in quiete, ma abbiamo detto che non è in quiete rispetto a nessuno.
In secondo luogo , dire "il fotone non ha massa di riposo" sembrerebbe aprire uno spiraglio alla possibilità che abbia una massa quando è in moto . Ma è sempre in moto , e questa possibilità non sussiste .
Per una particella materiale , di massa m , l'energia e la quantità di moto relativistiche sono date rispettivamente da :
per cui il rapporto vale :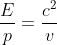 , e ci siamo liberati sia di
, e ci siamo liberati sia di 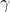 che di m . Per il fotone , ponendo c al posto di v al denominatore , si ha :
che di m . Per il fotone , ponendo c al posto di v al denominatore , si ha : 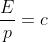 , da cui :
, da cui : 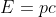 .
.
Inoltre , siccome per una particella materiale la componente temporale del 4-vettore impulso è uguale a ,
,
nel caso del fotone si ha che :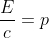 . In sostanza, per il fotone l'energia e la quantità di moto sono uguali.
. In sostanza, per il fotone l'energia e la quantità di moto sono uguali.
tutte cose dette e ridette nell'approfondimento sulla DR... Comunque la ma era una specie di provocazione che, pensa te, aveva usato perfino Feynman... che non è un povero sprovveduto come Zappalà...
Da Pippo: "nel caso del fotone si ha che :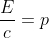 . In sostanza, per il fotone l'energia e la quantità di moto sono uguali."
. In sostanza, per il fotone l'energia e la quantità di moto sono uguali."
È troppo chiedere che significa, naturalmente se non è troppo lungo e complicato. Nel frattempo mi "studio" la Dinamica Relativistica.
caro Gimar,
intanto mi complimento con te per la passione che ci stai mettendo. La dinamica relativistica è fondamentale per capire il comportamento del fotone, ma non solo.
In realtà, più ci avviciniamo a velocità ultrarelativistiche, e più l'uguaglianza tra quantità di moto ed energia è vera. Basta scegliere le giuste unità di misura. E = mc^2, ma q = mv e se v si avvicina a c si ha che E = q/c. Se si considera c = 1 si ha l'uguaglianza che per il fotone è perfetta. Tuttavia, resta il fatto un po' ambiguo dell'essenza stessa della massa relativistica, su cui abbiamo discusso a lungo... Comunque, ti consiglio di non cercare di capire solo attraverso commenti parziali e privi di collegamento alla problematica generale, che non riescono a dare un quadro della situazione. Proprio per questo "odio" i forum dove ognuna infila quello che sa senza fare un discorso unitario. Segui la strada che hai scelto e dedicati alla dinamica relativistica. Vedrai quanto è bella e quanto riesca a spiegare, partendo dalla RR che sembra quasi un qualcosa di immaginario e non realistico... L'uguaglianza tra massa ed energia o quello che in realtà vuole significare ha cambiato la visione dell'Universo, ricordiamocelo sempre...
Comunque sia, grazie per la voglia di imparare... mi ripaga del tempo speso a scrivere gli approfondimenti!
Vincenzo
io posso anche scrivere 50 pagine, a partire dai concetti di inerzia , energia, quantità di moto in meccanica classica, per poi passare alla relatività e alla modificazione dei concetti ora detti.
Ma sarebbe solo un doppione di quanto hai scritto tu, no?
Nei forum succede anche di molto peggio, gente incompetente scrive su argomenti che non conosce o conosce poco e male.