Categorie: Fenomeni astronomici Relatività
Tags: aberrazione della luce quiz relatività galileiana relatività ristretta velocità
Scritto da: Vincenzo Zappalà
Commenti:14
Aberrazione della luce. 5: QUIZ: capiamo bene l’orologio di luce **
Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.
Per costruire ciò che si vede da un’astronave, dobbiamo tornare un po’ indietro (alle basi della RR) e analizzare un po’ meglio l’orologio di luce. Sembra facilissimo costruirlo e paragonare immediatamente le velocità coinvolte. Una è sicuramente quella della luce e l’altra è quella di chi muove. Tuttavia, stiamo bene attenti a non arrivare a conclusioni errate guardando la classica figura galileiana… Un piccolo quiz per rinfrescare la memoria
Mettiamoci nelle condizioni di uno spazio galileiano, dove le velocità si sommano senza problemi e disegniamo la Fig. 1
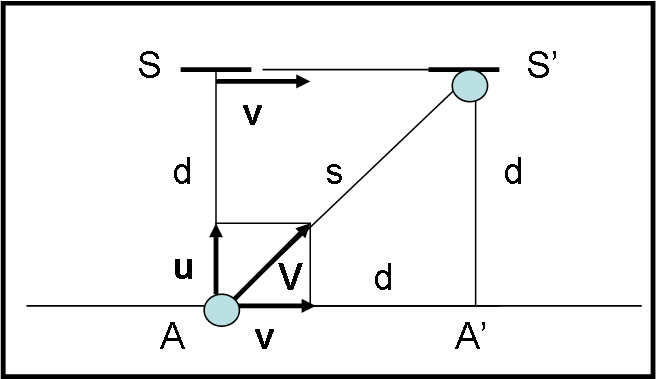
Noi assistiamo al moto di A che ha sopra di sé uno specchietto S, posto a una certa altezza d. Entrambi si muovono solidalmente con velocità v verso destra. Il viaggiatore A ha una pallina P in mano (che, quindi, si muove anch’essa con velocità v). In A viene lanciata la pallina P esattamente in verticale con una certa velocità u. Non sappiamo, però, quanto vale questa velocità. Tuttavia, se quando A arriva in A’, percorrendo una distanza d, la pallina raggiunge esattamente lo specchietto che si è portato in S’, possiamo ricavare immediatamente la velocità u. Infatti, nello stesso tempo t in cui il personaggio si è spostato di d (AA’), la Pallina si è spostata, in verticale, di AS = A’S’ = d. Possiamo scrivere:
u = d/t per la pallina
v = d/t per il viaggiatore A
I secondi membri sono uguali e, quindi, u = v. Alla stessa conclusione si arriva direttamente attraverso la somma di due vettori. In particolare, possiamo dire che la pallina ha viaggiato in diagonale (distanza s) con una velocità V, il cui modulo è uguale a:
V2 = u2 + v2 = v2 + v2 = 2v2
V = √2 v
Abbiamo trovato questa ovvia soluzione imponendo, praticamente, che il tempo sia lo stesso sia per il viaggiatore che per noi che guardiamo la scena da fermi.
Immaginiamo, adesso, di utilizzare un fotone F al posto della pallina P. Immaginiamo, anche, che la configurazione sia perfettamente uguale a quella di Fig. 1 e la riportiamo in Fig. 2.
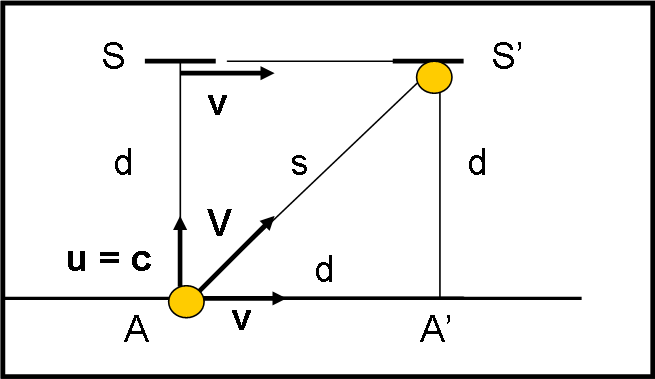
Lo spazio, percorso da A ad A’, è sempre uguale a d, ma quanto vale la velocità v, rispetto a quella del fotone u = c ? Ossia quanto vale v/c? Non mi direte certo che vale di nuovo v = c...
QUI la soluzione






14 commenti
Mi butto (forse nel vuoto 8-O)... dopo aver riletto la lezione sull'orologio a luce (RR fig. 26 e seguenti) e applicato le stesse formule della fig. 27 al quiz proposto:
d=vt AS'=ct
applico Pitagora al triangolo AA'S':
AS'2 = AA'2+A'S'2 ovvero, sostituendo:
c2t2 = d2+d2 = v2t2+v2t2 = 2v2t2
v2 = c2t2/2t2
v = 1/2c√2
Ma nooooo... sono spariti tutti gli apici!!!
Comunque tutti i 2 presenti in queste espressioni sono apici, tranne quello rosso che è coefficiente di v
c2t2 = d2+d2 = v2t2+v2t2 = 2v2t2
v2 = c2t2/2t2
Il risultato è
v = 1/2c√2
Radice quadrata di 1 -(V/c) al quadrato
non voglio dire niente, ma ricordatevi che i tempi non sono uguali nei due sistemi...
Voglio essere più chiaro...
quando è stato applicato il teorema di Pitagora, è stato messo A'S' = vt. Ma chi l'ha detto che la velocità è v... a me sembra che sia c..., ossia d verticale deve essere ct... e allora viene fuori che v = c... I tempi, i tempi...
Non guardiamo il risultato finale... ma guardiamo di seguire le regole della RR, anche se è un po' più intricata (ma ben poco).
Ma d verticale vale ct' nel tempo proprio dello specchio in movimento. Per chi sta "fermo"
d=d = vt
ma la diagonale nel sistema fermo vale ct , questo per permettere all'evento riflessione in S' di essere coerente con quello del sistema in movimento al "suo" tempo ct'
quindi
da cui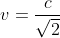
boh ....
caro Leandro,
in realtà il d verticale vale ct', mentre il d orizzontale vale vt... se t fosse lo stesso avremmo c = v...
cari amici,
il succo del discorso sembrerebbe da vero pignolo... Ma, sono convinto che mi capirete... Non possiamo uguagliare patate con cavoli. Prima dobbiamo trasformare tutto in cavoli o tutto in patate. Poi si può anche uguagliare... non fatemi arrabbiare Albertino!
Caro Enzo, ci provo anch'io.
Prima però vorrei fare una premessa: il moto del viaggiatore avviene solo sull'asse x, per cui la distanza d verticale è uguale sia per il sistema considerato fermo, sia per il viaggiatore.
Per quest'ultimo, il fotone percorre la distanza verticale d in un certo tempo t', alla velocità della luce, ossia:
d = ct'
Per il sistema considerato fermo il viaggiatore percorre la distanza d (che per lui coincide con d verticale) in un certo intervallo di tempo misurato nel suo sistema (come se ci fossero due orologi sincronizzati uno in A e l'altro in A'), ossia: d = vt
Vista dal sistema fermo la distanza d è lo stessa, ossia:
ct' = vt
v = c t'/t
Le trasformazioni di Lorentz, consentono di confrontare queste due intervalli di tempo, misurati da due sistemi diversi, ossia:
Δt = Δtp 1/√ (1- v²/c²)
Δtp = Δt√ (1- v²/c²)
Quindi, basta sostituire t' al tempo proprio Δtp misurato dal viaggiatore e t al tempo Δt misurato dal sistema considerato fermo :
t '= t √ (1- v²/c²)
Sostituendo t' nella relazione tra velocità, trovata prima, si ottiene:
v = c t'/t
v = c t √ (1- v²/c²)/t
v = c √ (1- v²/c²)
Per controllare se tutto funziona basta vedere qual è il percorso del fotone visto dal sistema fermo, ossia:
AS' = S = c t
Usando il teorema di Pitagora con le velocità ottenute prima, si ottiene la velocità del fotone visto dal sistema considerato fermo:
V² = v² + c² (1- v²/c²) = v² + c² (c²- v²)/c² = v² + (c²- v²) = c²
V = c
Quindi anche per il sistema fermo la velocità del fotone è uguale a C... d'altronde la velocità della luce è costante ed uguale misurata da qualunque sistema di riferimento.
Paolo
Dimenticavo , volendo si può ulteriormente sviluppare questo rapporto:
, volendo si può ulteriormente sviluppare questo rapporto:
v = c √ (1- v²/c²)
v/c= √ (1- v²/c²)
v²/c²= 1- v²/c²
v²/c² + v²/c² = 1
2 v²/c² = 1
v²/c² = ½ = 0,5
v/c = √0,5
D'altronde se si prende in considerazione, nel sistema fermo, il triangolo AA'S', per il teorema di Pitagora:
AS'² = d² + d²
AS'² = 2d²
ma d=vt e AS' = ct
c²t² = 2v²t²
c² = 2v²
v²/c² = ½ =0,5
v/c = √0,5
Paolo
devo dire che, come sempre Paolo, ha importato bene tutta la questione... Tuttavia, torno a dire che l'ultima parte non mi piace. Anche il lato verticale viene indicato vt e questo non è vero, lui è ct, mentre quello orizzontale e' vt', Tutto ciò potrei anche farlo disegnando il triangolo in un sistema fermo, ma non osservandolo mentre avviene durante il moto...
Va bene, comunque, il succo è stato sviscerato... a fine settimana darò la mia versione, quella che mi sembra più corretta.
Sapete, sto facendo tutto questo per poter disegnare convenientemente l'ellisse di aberrazione, mettendo le giuste quantità nei vari segmenti e non confondersi, Lì, sì che si potrebbe commettere un errore...
cari tutti,
ho anticipato la soluzione (o, meglio, l'interpretazione) perché mi stavo accorgendo di creare confusione inutile. In fondo, la soluzione è giusta e io mi ero solo impuntato su una definizione più omogenea. Il tutto voleva solo far capire che il segmento orizzontale uguale a quello verticale non può dirci che v = c...
Abbiate pazienza...
Scusa Enzo vediamo se ho capito cosa intendi sull'ultima parte.
Sempre guardando dal sistema fermo il solito triangolo AA'S'.
La distanza d, orizzontale è uguale a vt:
AA' = vt
La distanza d, verticale è uguale a ct':
AS =A'S'= ct' = ct √ (1- v²/c²)
Se provo a ricavare l'ipotenusa del triangolo AS', ottengo:
AS'² = AA' ² + A'S' ²
AS'² = v²t² + c²t² (1- v²/c²)
AS'² = v²t² + c²t² (c²- v²)/c²
AS'² = v²t² + t² (c²- v²)
AS'² = v²t² + c²t² – v²t²
AS'² = c²t²
AS' = ct
Ottengo che per il sistema fermo il tragitto AS' viene percorso dal fotone alla velocità c.
Vorrei capire meglio se anche così non è corretto...
Paolo
lascia stare Paolo ... non voglio creare più confusione... ho scritto già quello che intendevo...