Categorie: Buchi neri Relatività
Tags: getti relativistici Pappo parte visibile di una sfera. Pippo quiz torta gelato sferica velocità della luce velocità di espansione visioni relativistiche
Scritto da: Vincenzo Zappalà
Commenti:16
Soluzione del quiz della torta sferica e sua applicazione ai getti relativistici **/***
Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante.
Il quiz è stato velocemente risolto dai nostro soliti “maghi” & co., ma, malgrado sia giunto il momento di descrivere compiutamente la soluzione, invito chi non abbia ancora avuto l’intuizione, di proseguire, comunque, a pensare e a non leggere subito questo articolo. Capire da soli il meccanismo di base, aiuterà sicuramente nel prosieguo della problematica, tra le più interessanti e imprevedibili della fisica relativistica. Quando velocità relativistiche si mischiano alla “lentezza” della velocità della luce, tutto può succedere, anche le magie delle favole!
Avrete già capito che questa serie di QUIZ, legati alla visione "apparente" di strutture più o meno semplici che mostrano velocità relativistiche, giocano un ruolo importantissimo nel descrivere come gli effetti della RR (soprattutto la contrazione delle lunghezze) siano completamente deformati quando siano realmente visti o -meglio- fotografati da un osservatore appartenente a un altro sistema di riferimento.
Vi posso dire che questa problematica ha dato il via a molte discussioni, ripensamenti, dispute anche accese, che durano tuttora. Noi andremo avanti mantenendo l’intera trattazione su livelli semplici e comprensibili a tutti, tralasciando le formulazioni matematiche più complesse che hanno coinvolto personaggi del calibro di Terrell e Penrose. Alla fine (il percorso è tutt’altro che finito) potremo mettere insieme, negli approfondimenti, un argomento poco conosciuto, ma estremamente stimolante e ricco di numerose sfaccettature. Concluderemo con uno dei “miracoli” (apparenti) della Natura: deformatela come volete, ma una sfera che viaggia a grandissima velocità rimane una sfera! Tutto ciò che l’ha deformata, allungata, accorciata, ecc., ecc. si nota solo se si ha l’accortezza di dipingerla in modo da capire quale emisfero si stia realmente vedendo.
Ma torniamo a noi, dato che la strada è ancora abbastanza lunga. Abbiamo già imparato una cosa fondamentale: la luce, l’informazione regina per conoscere l’Universo, è capace di giocarci tiri mancini, non solo a livello microscopico. Sarebbe molto meglio il “tatto”, attraverso il quale la misura di un qualcosa non sarebbe influenzata dalla lentezza della luce. Sarebbe, ovviamente… ma è del tutto assurdo pensare di credere solo in quello che si tocca, quando le distanze in gioco sono fuori dalla portata di qualsiasi “mano” cosmica. L’esplorazione spaziale e le immagini dei massimi telescopi e dei più accurati microscopi hanno bisogno della luce. Ne segue che quella che sembrerebbe una realtà deformata diventa la realtà con cui dobbiamo scontrarci. Non resta che capire le deformazioni e fare un passo indietro, ma non sempre la faccenda è così banale… anzi!
Un gioco di prestigio diventa la normalità e la normalità il vero trucco da scoprire. D’altra parte la RR ci ha già messo di fronte a situazioni del genere. Pensiamo al muone: lui non potrebbe arrivare a terra e invece ci riesce e ne abbiamo la certezza “pratica”. Una magia che diventa realtà fisica. Immaginiamo di aggiungere a questo fenomeno quasi paranormale, tutti gli effetti dovuti a quei giocherelloni dei fotoni e alla loro velocità di crociera di tutto riposo: se gli oggetti coinvolti avessero dimensioni non trascurabili, la magia apparente supererebbe la magia reale. Un vero caos.
Per darvi un’idea di quanto tutto ciò sia, anche se quasi completamente inosservabile, una pura stregoneria quotidiana, pensiamo a una velocità della luce di soli 30 km/h. Il mondo attorno a noi sarebbe un vero incubo (abbiamo parlato QUI di cosa cambierebbe nella nostra visione dell'Universo, se la velocità della luce fosse diversa da quella che è)
Bando alle ciance (si fa per dire…) e torniamo ai nostri due amici, Pappo e Pippo.
Lo strumento geniale di Pappo non è altro che una specie di “ago” per palloni da calcio, unito a una pompa ancora più speciale. In tal modo (almeno ai miei tempi) si gonfiavano i palloni di cuoio. L’unica vera differenza è che la pompa di Pappo è veramente potentissima e permette al pallone-torta di gonfiarsi, ossia di espandersi, a velocità relativistica. Non sbagliate di certo se pensate all’espansione dell’Universo (il quiz originario l’avevo proprio impostato su questo, ma poi sorgevano difficoltà troppo grandi per mantenere analogie soddisfacenti e non travisanti). Un Universo colorato in modo geometrico…
Capite anche perché è bene che Pippo risponda abbastanza in fretta, altrimenti la torta esploderà in mille pezzi! La mamma dei due ragazzi è un'ottima cuoca, ma la sua "pasta" non può competere con lo spazio dell'universo...
L’unico concetto da comprendere fin dall’inizio è che la luce che viaggia verso Pippo deve seguire un andamento orizzontale, mentre la superficie della torta sferica s’ingrandisce radialmente, mantenendo sempre lo stesso centro, ma aumentando il proprio raggio R di un fattore dR = v dt (dove dt è un certo tempo prefissato, ad esempio scelto come unità). Ma tralasciamo del tutto le formule, anche se semplici, e utilizziamo la semplice Fig. 1.
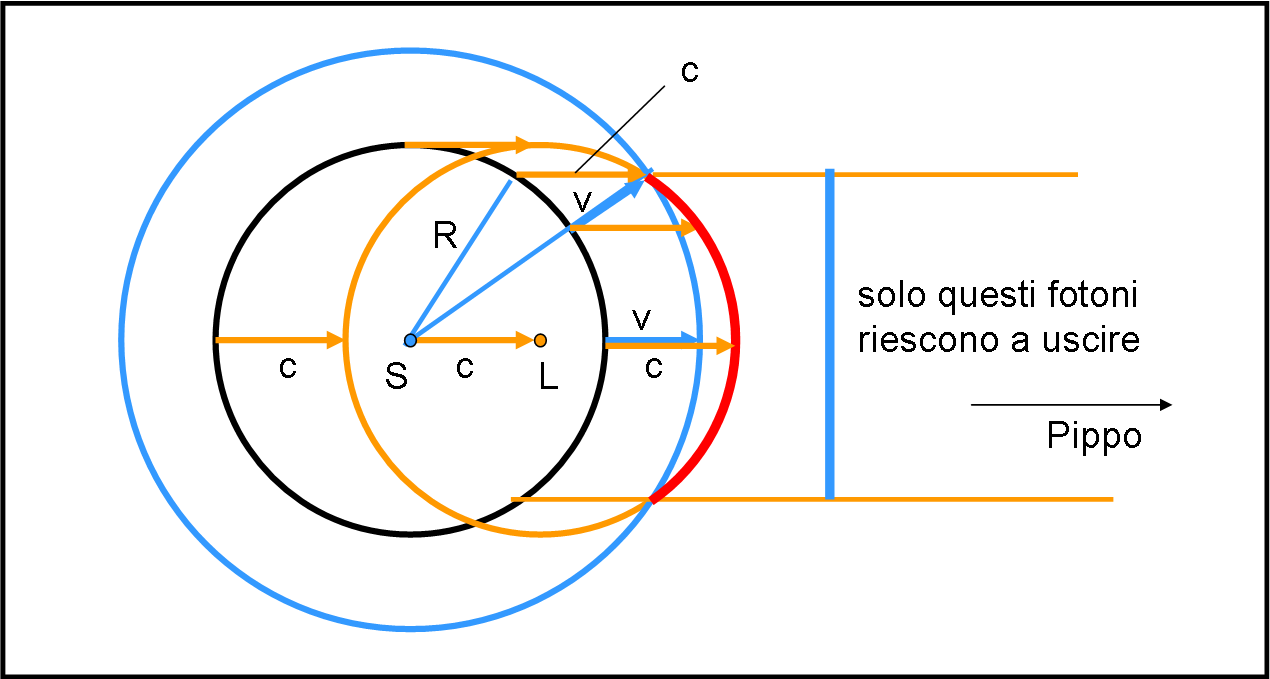
La torta sfera (cava) originaria è il cerchio nero. Pappo inserisce la sua pompa relativistica e permette alla torta di dilatarsi, in un certo tempo dt, fino a diventare il cerchio azzurro. In un tempo unitario (dt = 1) l’aumento del raggio della sfera cava è esattamente dR = v, indicato dalle frecce azzurre. Qualsiasi raggio si consideri, esso si è allungato radialmente della stessa quantità. Insomma la torta nera è diventata la torta azzurra.
Tuttavia, nello stesso tempo dt = 1, anche i fotoni sono partiti dalla sfera originaria. Essi si muovono in senso orizzontale (devono raggiungere Pippo) di una lunghezza pari a c dt = c = velocità della luce. v è decisamente più bassa di c, ma cosa capita al fotone che parte dal punto più alto della sfera (o da quello più basso)? Per veloce che vada non riesce a raggiungere la parte interna della superficie della torta che si è portata più avanti. In qualche modo, rimane intrappolata dentro alla torta e mai ,nel tempo dt, raggiungerà Pippo, ossia Pippo mai riuscirà a vedere quel punto della sfera: nel tempo dt, il fotone sarà sempre indietro rispetto alla superficie della torta.
Ma non è solo quel fotone a subire questa sconfitta… Per generalizzare il tutto in modo immediato, disegniamo un altro cerchio, ossia quello che raffigura la posizione, al tempo dt = 1, dei fotoni lanciati dalla sfera al tempo iniziale. Questo cerchio è di banale costruzione: basta prendere la torta e spostare il suo centro di una lunghezza pari a c (cerchio arancione), come la figura mostra meglio di tante parole.
A questo punto abbiamo a disposizione due circonferenze fondamentali: quella della torta espansa in un tempo unitario e quella relativa al punto di arrivo di tutti i fotoni dopo lo stesso tempo dt = 1.
Come facciamo a vedere quali sono i fotoni che sono riusciti a essere più veloci dell’espansione della sfera? Basta intersecare i due cerchi (azzurro e arancione) e la parte rossa (del cerchio arancione) che rimane più avanti di quella azzurra rappresenta il gruppo di eroici fotoni che si dirigono senza più problemi verso Pippo.
Attenzione: questi fotoni non hanno certo attraversato la torta, ma sono sempre stati avanti rispetto a lei. I fotoni rimasti indietro possono al limite toccare la superficie interna della torta, ma non certo attraversarla. E se toccassero la parte interna... sparirebbero.
Dopo un altro tempo dt = 1, la situazione si ripete tale e quale (è come se prendessimo una torta più grande e ripetessimo l’esercizio). L’importante è considerare i nuovi fotoni inviati dalla torta dopo dt = 1 e non più quelli iniziali che sono già stati “scremati”. Come la faccenda si evolva a noi interessa poco, dato che i fotoni che ci interessano sono quelli del primo lancio.
Una piccola aggiunta… In realtà, i fotoni delle parti più esterne della zona interessata devono partire poco prima di quelli centrali per giungere insieme a loro da Pippo. Poco male… basta solo fare partire un po’ dopo quelli centrali (tanto sono liberi di farlo dopo un minimo intervallo di tempo, nessuno li ferma) e si aggregano perfettamente a quelli laterali. E’ il nostro righello verticale al contrario… parte leggermente curvo e dobbiamo aspettare che diventi rettilineo. Tuttavia, si può benissimo tralasciare questo effetto di ordine superiore…
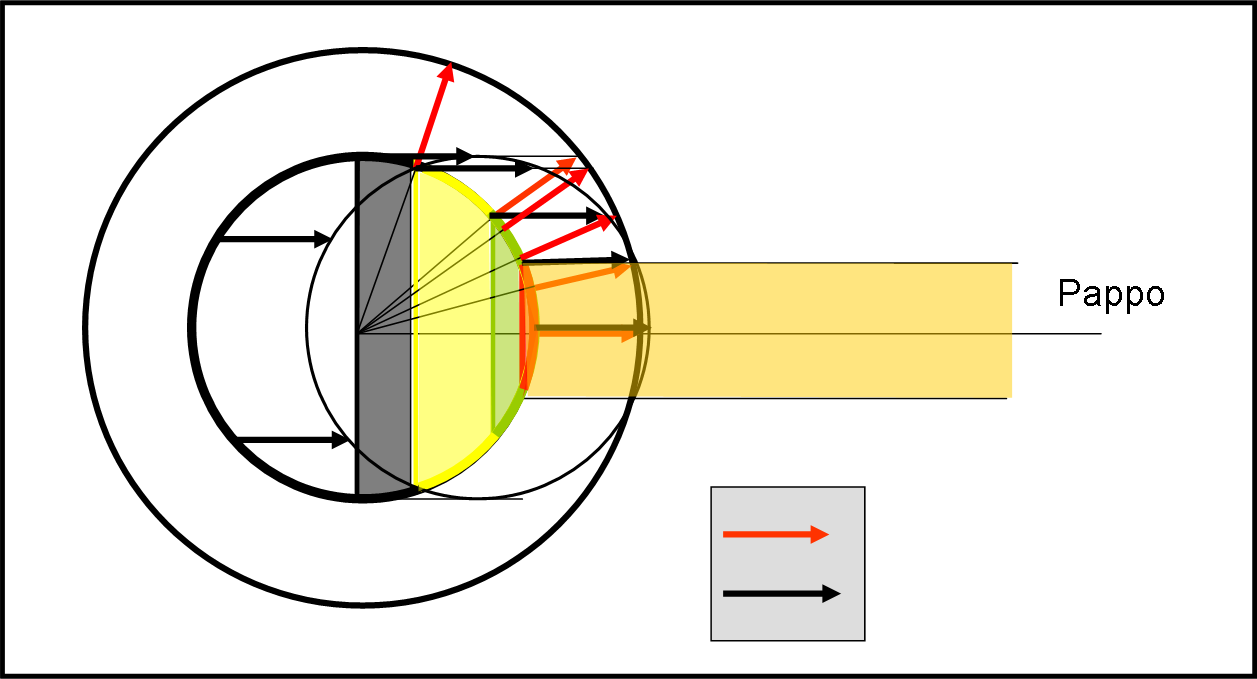
Il succo di tutto è che il nostro Pippo è costretto a vedere solo la parte centrale rossa della torta, dato che i fotoni degli altri colori non riescono a uscire allo scoperto. Quanta parte della sfera sia visibile dipende, ovviamente dalla velocità di espansione. Affinché Pippo rimanga a bocca asciutta è necessario scegliere la v giusta, cosa che Pappo ha saputo fare con grande precisione e che è illustrata in Fig. 2.
Qui di seguito il video di Arturo (che ringrazio apertamente). A noi interessa, ovviamente, solo la prima parte

Risolto il quiz, diamone una interpretazione ben più generale e… astrofisica.
Una sfera, che si espande a velocità relativistiche, viene vista solo parzialmente da un osservatore molto distante (non prendiamolo vicino se no le cose si complicano troppo, pur non cambiando il succo). Ciò che si vede è solo la parte centrale, sempre più piccola al crescere della velocità di espansione. Teoricamente, per v = c, vedremmo solo un punto della sfera. Ho recuperato la bella figura che segue (Fig. 3), che ci mostra con le giuste misure una sfera che si espande a velocità crescenti. Per evidenziare il restringimento della zona visibile, la sfera è stata disegnata a scacchi chiari e scuri. La prima velocità è nulla, la seconda è pari al 70% della velocità della luce, la terza al 90% e la quarta al 99%.
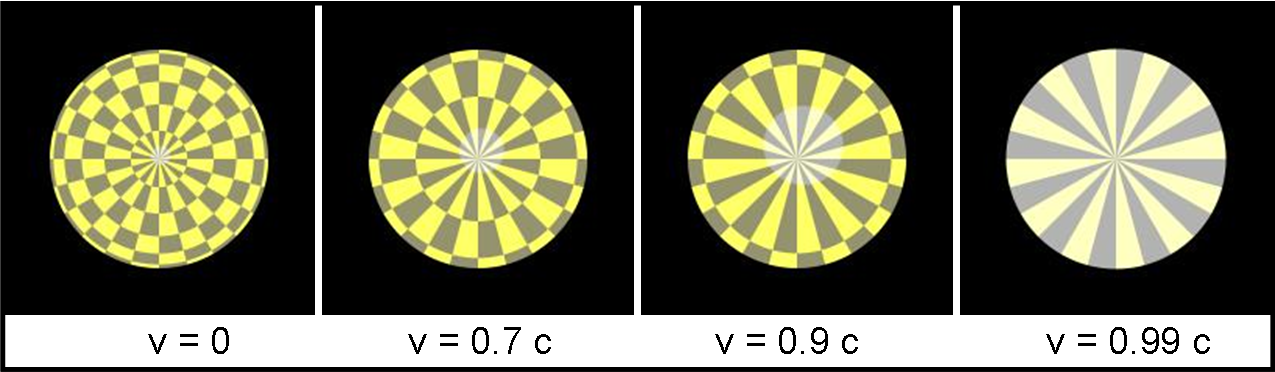
Noterete che vi è anche una zona circolare leggermente più chiara che all’inizio è collocata al centro come una macchiolina e che alla fine copre l’intera parte visibile. Questa macchiolina introduce al discorso sui getti relativistici del buchi neri galattici.
Più o meno sappiamo come si originano, attraverso la caduta del disco di accrescimento verso il buco nero e la sua interazione col campo magnetico (effetto sincrotrone) che serve come lanciatore efficientissimo. Fatto sta che le particelle che li compongono viaggiano a velocità decisamente prossime a quelle della luce. Tuttavia, succede proprio il contrario della torta-sfera di Pappo.
I getti si scontrano con il mezzo intergalattico, si alza la loro temperatura e diventano estremamente luminosi nei raggi gamma (in altre parole non se ne ha una visione diretta, ma solo ricostruibile dalla luminosità che perviene all’osservatore). Tuttavia, l’urto smorza la velocità e di conseguenza anche la luminosità del getto.
Cosa succede realmente?
Facciamo due ipotesi:
(1) Il getto è perfettamente sferico e quindi dovrebbe mostrarci una semisfera illuminata. Tuttavia, a causa dell’effetto che abbiamo appena imparato, la superficie illuminata continua ad aumentare dato che la velocità decresce e si vede una zona sempre più ampia di superficie sferica. Vi sono, perciò due effetti che giocano in contemporanea: la decrescita continua della luminosità intrinseca (calo di temperatura) ma anche un aumento continuo di superficie illuminata. I due effetti comportano una curva di luce (ossia un decremento della luminosità) non troppo ripida, dato che i due effetti giocano in modo opposto. Alla fine, la sfera è tutta visibile, ma la luminosità ha smesso di essere registrabile (il getto ha esaurito la sua capacità di inviare raggi gamma).
(2) Il getto è simile a un cono con superficie esterna sferica. Tuttavia, esso è sempre tutto visibile fin dall’inizio (è molto collimato). Ne segue che la parte illuminata non aumenta al decrescere della velocità di espansione: la decrescita è solo dovuta alla diminuzione intrinseca della luminosità. L’andamento decrescente della curva di luce è nuovamente costante, ma più ripido di quello precedente, in quanto non gioca affatto l’aumento dell’area visibile (si vede tutta fin dall’inizio).
Le due ipotesi, però, potrebbero convivere. Infatti, all’inizio la velocità di espansione è talmente alta che è visibile sono una parte del getto collimato. Al decrescere della velocità, la parte visibile aumenta e quindi siamo nella ipotesi (1): la diminuzione della luminosità non è troppo ripida. A un certo momento, però, tutta la superficie esterna del getto risulta visibile e si innesca il meccanismo (2): la decrescita è più ripida perché dipende solo dalla diminuzione intrinseca della luminosità.
In quest’ultimo caso avremmo la certezza che il getto non è sferico, ma collimato, e avremmo molte informazioni sulla sua velocità e larghezza. Di seguito mostriamo, come prova REALE e misurabile, la curva di luce di un getto di un buco nero galattico in funzione del tempo, riguardante il lampo gamma GRB 990510 (Fig. 4). L’andamento decrescente subisce un brusco cambiamento di pendenza, che viene chiamato in gergo “jet break”. La prova di essere di fronte a un getto e non a una bolla sferica e tante altre informazioni di non facile determinazione sono servite. Altro che la sfera-gelato di Pippo e Pappo!
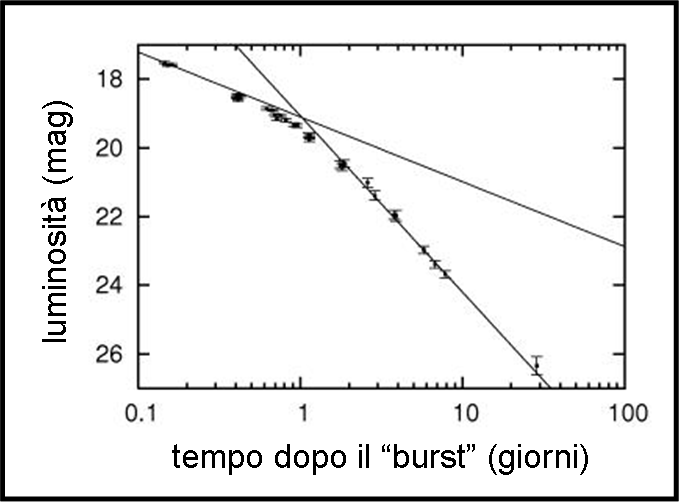
Ritorniamo a bomba: siamo ancora sicuri che le deformazioni dovute alla limitatezza della velocità della luce, in campo relativistico, siano solo … illusioni e non abbiano risvolti pratici interessantissimi ?
Non abbandonate questa serie di articoli… ne vedremo ancora delle belle!






16 commenti
Bellissima spiegazione, Vincenzo, anche per la parte riguardante l'applicazione ai getti dei buchi neri. Grazie a te !
Solo come curiosità, visto che mi è servito conoscerlo nella realizzazione dell'animazione che hai inserito nell'articolo, l'istante di tempo al quale il fotone FF raggiunge la parte interna della sfera in espansione è dato dalla formula:
essendo R il raggio iniziale della sfera, l'angolo al centro sotteso dall'arco verde. Ci sono arrivato con semplici applicazioni della cinematica del punto in moto rettilineo uniforme e della geometria
l'angolo al centro sotteso dall'arco verde. Ci sono arrivato con semplici applicazioni della cinematica del punto in moto rettilineo uniforme e della geometria 
"cosa capita al fotone che parte dal punto più alto della sfera (o da quello più basso)? Per veloce che vada non riesce a raggiungere la parte interna della superficie della torta che si è portata più avanti. In qualche modo, rimane intrappolata dentro alla torta e mai raggiungerà Pippo, ossia Pappo mai riuscirà a vedere quel punto della sfera: il fotone sarà sempre indietro rispetto alla superficie della torta."
Se ho ben interpretato l'articolo, questa affermazione dovrebbe essere vera nell'intervallo dt considerato in fig.1, giusto?
Mi spiego meglio: se la torta fosse fatta di un materiale permeabile ai fotoni e infinitamente elastico che consentisse un'espansione illimitata, essendo la velocità di espansione inferiore a quella della luce, prima o poi i fotoni che sono rimasti all'interno nell'istante iniziale, dovrebbero uscire ed essere visibili da Pippo... o sbaglio?
cara Dany,
prima o poi il fotone arriverà, anche perché niente può restare costantemente a una certa velocità e deve diminuirla. Questo è il vero succo. In realtà, non ci sarà mai una tela invalicabile, ma solo un percorso più lungo da fare per mettersi in luce, oppure uno scontro all'interno del getto. Noi abbiamo fatto un caso teorico, che, però, ha una sua applicazione più che concreta, in quanto per alcune ore il getto aumenta realmente la sua superficie visibile...
caro Arturo,
direi che è esatta e mi sembra proprio il punto di partenza per molti studi un "po'" eretici (che ho tralasciato...) che portano a una rivisitazione della RR. Ma noi andiamo avanti con le cose meno fantasiose (per questo argomento almeno)... Sono contento che l'argomento ti piaccia!
Si , molto interessante davvero. Che altro ci dobbiamo aspettare?
Grazie, Enzo!!!!
Beh..., caro Mau, ad esempio, mettere in moto un cubo o anche solo un quadrato e guardarlo fuori dalla retta del suo spostamento. Ma non un quadrato perpendicolare all'asse ottico, bensì sul piano della figura...
Molto interessante il quiz e l'applicazione ai getti relativistici.
Dalla figura 1 si può ricavare che la velocità di espansione verso l'osservatore della parte più esterna della sfera è superiore alla velocità della luce?
Non ci sarebbe nessun problema per la relatività poichè questa velocità "apparente" è dovuta all'effetto combinato delle velocità radiali di diverse parti di materia, con le velocità radiali tutte minori di c.
Mi ricorda il quiz di qualche mese fa sulle ombre che viaggiano a velocità superiore alla luce, ma qui gli effetti sono più concreti.
In realtà, Fabry, non è proprio giusto. La luce parte da punti arretrati rispetto a quelli che comandano l'espansione. Un punto qualsiasi della superficie si espande con una velocità sempre minore di c. E' solo un problema di componenti... Sempre che abbia capito esattamente cosa vuoi dire...
Provo a illustrare meglio quello che intendevo dire.
Supponiamo di essere nella fase di espansione radiale a velocità costante.
Il percorso che dovrebbe fare un fotone emesso dalla superficie della sfera per raggiungere l’osservatore molto remoto è parallelo all’asse x della figura. Considero uno di questi fotoni emesso in un certo istante da un punto P della superficie della sfera che si trova a una distanza h dall’asse x. Mi domando quale è la velocità di espansione della sfera lungo il tragitto che dovrebbe seguire il fotone. Chiamo questa velocità u e chiamo v la velocità di espansione radiale.
La velocità u risulta dall'effetto combinato di diversi elementi di materia tutti che si muovono radialmente a velocità v. Non è la componente di v lungo l'asse x.
Per il momento mi accontento di trovare u proprio nel momento della emissione del fotone.
Intano il legame tra x(t) ed R(t) è:^2=R(t)^2-h^2) . Si può ottenere u derivando rispetto al tempo questa relazione.
. Si può ottenere u derivando rispetto al tempo questa relazione.
Un altro modo è quello di considerare questa figura, sfruttando la similitudine tra il triangolo più grande e quello più piccolo.
Per un certo h, u diventa maggiore di c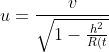^2}}}>c)
Questo accada per\sqrt{1-\frac{v^2}{c^2}}) . Nessun problema per la relatività poichè si tratta dell'effetto combinato di diversi elementi di materia tutti che viggiano a velocità minore di c.
. Nessun problema per la relatività poichè si tratta dell'effetto combinato di diversi elementi di materia tutti che viggiano a velocità minore di c.
I fotoni emessi verso l'osservatore da una distanza dall'asse x maggiore di h vengono immediatamente riacciuffati dalla sfera in espansione e non riescono a propagarsi verso l'osservatore.
Un fotone invece riesce a sfuggire se è emesso dalla superficie della sfera entro la distanza h dall'asse x. Se inizialmente sfugge, non può più essere ripreso dalla sfera in espansione. Almeno secondo la formula sopra dove risulterebbe che, a parità di h, u decresce con l'espansione della sfera anche se la velocità di espansione radiale v rimanesse costante, tanto più se v diminuisce.
caro Fabry,
ma, in pratica, non sarebbe altro che l'intersezione tra le due sfere della Fig. 1? Per poter scappare il fotone dovrebbe superare c... ed è per quello che resta indietro...
Adesso devo andare a camminare, ci penso meglio quando torno...
Forse ho capito Fabry dove sta il piccolo inghippo... Tu consideri una componente dell'espansione parallela all'asse x (u mi sembra). Ma quella non è una componente, in quanto il punto P a cui è applicata si muove solo in senso radiale (questo vettore velocità darebbe la vera componente del moto del punto lungo la x). Il vettore u non è altro che la differenza tra due punti della sfera, uno prima e uno dopo l'espansione. Essendo due punti separati la loro distanza non ha niente a che vedere con una velocità...
Sono di corsa... e quindi potrei anche aver capito male... quando torno ci studio meglio sopra...
Bene,
ho riletto con maggiore attenzione la tua descrizione e direi che arriviamo alla stessa conclusione. u è l'ipotetica velocità di un fotone che volesse raggiungere, comunque, la sfera. Ovviamente. la stessa cosa si può esprimere dicendo che si cerca il punto in cui il fotone riesce a raggiungere la sfera, che è proprio l'intersezione tra le due sfere di fig. 1. E' solo questione di capirsi ...
Certo, come dicevo nel mio primo messaggio, il mio ragionamento mi sembrava già contenuto nella tua figura 1. L'ho solo messo per esteso per farmi capire. Volevo solo accertarmi che il fenomeno potesse essere interpretato come dovuto al crearsi di una velocità di espansione "apparente" maggiore di c lungo la direzione di propagazione del fotone diretto verso l'osservatore.
perfetto Fabry... ho solo fatto un po' di confusione (l'età... )
)
....se quello che scrivi la chiami confusione, mi picerebbe ce ne fosse tanta in giro di questa "confusione".