Categorie: Relatività
Tags: astronavi di Bell Bell Flores paradossi relativistici quiz relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:19
Il Paradosso delle Astronavi di Bell: ultimo atto ***
QUI, QUI, QUI, QUI e QUI gli articoli riguardanti il paradosso delle astronavi di Bell che precedono questo
Quest’articolo è soprattutto dedicato alla traduzione di un articolo di Flores che riesce a descrivere la soluzione proposta dallo stesso Bell, utilizzando soltanto diagrammi spaziotemporali sia nel sistema di riferimento in moto che in quello in quiete. Si eliminano trattazioni di livello superiore, relative ai moti iperbolici e alle accelerazioni proprie. La conclusione è la rottura della corda per lo stesso motivo fisico. Pur ammettendo che il problema possa ammettere ancora possibili alternative e sia soggetto a critiche più o meno aleatorie, la mia fiducia in Bell è praticamente assoluto. Poi, ognuno, può scegliere la via che preferisce.
Ci sono varie strade per affrontare e per descrivere la relatività ristretta. Molte di queste sono più legate alla filosofia della Scienza piuttosto che alla Scienza stessa. La RR (relatività ristretta) è una rappresentazione della realtà o è proprio la realtà? L’esempio del muone sembrerebbe propendere per la seconda risposta. Inoltre, sembrerebbe che vi siano diverse realtà, che, probabilmente possono unificarsi solo e soltanto attraverso la comprensione di uno spaziotempo quadrimensionale. Troppo spesso, forse, si continua a separare la descrizione tridimensionale da quella temporale. Il che potrebbe portare a visioni distorte della vera realtà dell’Universo.
Aggiungiamo, inoltre, che l’introduzione di un’accelerazione non comporta immediatamente il passaggio da RR a RG (relatività generale). Senza la presenza di una massa che curvi effettivamente lo spaziotempo, un’accelerazione può sempre essere pensata come una serie di infinitesimi cambiamenti di velocità, trattabili ognuno con la RR. Proprio questa variazione continua può dar ragione di molti paradossi che ancora restano nell’ambito della RR. Sicuramente, tra questi, vi è il celebre e controverso paradosso delle astronavi di Bell.
Prima di iniziare la traduzione dell’ottimo lavoro di Flores, vorrei riassumere brevemente quanto avevo cercato di fare finora. Il paradosso fa uso di un’accelerazione continua, la quale però, nel caso del sistema di riferimento in quiete, non comporta nessuna apparente variazione rispetto al caso di una velocità costante. Dato che proprio la contrazione della corda e la non contrazione della distanza tra le astronavi assurge a punto veramente critico delle nostre discussioni (ma anche delle prime reazioni professionali al paradosso), avevo proposto una semplificazione valida solo per il sistema in quiete (corda applicata “al volo”). Se da un lato questo esempio illustra bene il problema della contrazione univoca, crea, però, un salto brutale nell’applicare alla corda una velocità v a partire dallo stato di riposo. Un qualcosa di “irrealistico”, anche se istruttivo. Tornando al paradosso originario, la faccenda si complica leggermente, ma mette in luce una trattazione ben più “realistica” della contrazione relativistica.
Traduzione dell’articolo “Bell’s spaceships: a useful relativistic paradox”(Le astronavi di Bell: un utile paradosso relativistico) di Francisco J. Flores (Università della California).
Di tanto in tanto ho aggiunto qualche nota personale per una migliore (spero) chiarezza o per rimandare a link presenti nel nostro archivio degli approfondimenti.
Il paradosso delle astronavi è particolarmente utile per gli studenti perché, pur considerando moti accelerati, può essere risolto con la semplice relatività ristretta e con l’utilizzo di facili diagrammi spaziotemporali. Inoltre, esso pone perfettamente in luce i problemi della relatività della simultaneità, della lunghezza propria e della “realtà” della contrazione di Lorentz.
Il paradosso
Bell propone di considerare tre astronavi, A, B e C, che vagano nello spazio privo di qualsiasi tipo di materia (niente attrazione gravitazionale). Le tre astronavi sono inizialmente in quiete, con B e C perfettamente equidistanti da A. Non appena B e C ricevono un segnale luminoso da A, esse cominciano ad accelerare “delicatamente”. Si assume che esse siano identiche, sotto tutti gli aspetti rilevanti per la trattazione, e che la programmazione delle accelerazioni che subiscono sia la stessa per entrambe.
Supponiamo di stendere una corda tra B e C (in due punti perfettamente equivalenti delle due astronavi), tale che essa sia esattamente uguale alla distanza tra i due punti delle astronavi, prima di essere messe in moto. L’apparente paradosso si riferisce al problema della rottura della corda.
Poiché B e C, e perciò anche la corda, iniziano a muoversi rispetto ad A, la lunghezza della corda dovrebbe accorciarsi a causa della contrazione di Lorentz. La corda, perciò dovrebbe rompersi. Tuttavia, un osservatore OA di A non può che concludere che la distanza tra B e C deve rimanere costante, dato che esse si muovono con la stessa accelerazione, ossia hanno la stessa velocità, istante per istante (RG trattata come RR). Questo fatto sembrerebbe dimostrare che la corda non si dovrebbe rompere.
La soluzione di Bell dice: “Come i razzi cambiano velocità, la corda diventa troppo corta, poiché deve continuamente contrarsi per effetto del fattore di Fitzgerald-Lorentz, fino a che sarà costretta a rompersi. Essa deve rompersi quando, per una velocità sufficientemente alta, la prevenzione artificiale della contrazione naturale (il legame con i razzi) impone stress intollerabili.”
Notiamo i due elementi didattici del paradosso. (1) Si vuole dimostrare che la corda si rompe, mentre non lo farebbe mai nello spazio newtoniano: una lezione già di per sé. (2) Si vuole dimostrare PERCHE’ la corda si rompe. E’ a questo punto che ci stacchiamo dalla strada seguita da Bell, in quanto la sua sottile spiegazione richiederebbe una buona familiarità con l’elettrodinamica relativistica, le integrazioni numeriche e varie importanti assunzioni sulla costituzione della materia.
Soluzione del paradosso
Si può dimostrare che, utilizzando solo diagrammi spaziotemporali elementari, le tre seguenti asserzioni sono VERE:
(1) L’osservatore OB di B e l’osservatore OC di C, concludono entrambi che la corda deve rompersi poiché: (a) OC misura che B rimane sempre più indietro; (b) OB misura che C si trova sempre più avanti.
(2) La distanza tra le due astronavi B e C, misurate da OA non cambia.
(3) OA conclude che la corda si deve rompere.
Nota: la prima asserzione si riferisce al sistema in moto con le astronavi, la seconda e la terza al sistema in quiete.
Per tracciare i diagrammi spaziotemporali necessari, si devono fare tre assunzioni. Innanzitutto, vengono soppresse due dimensioni spaziali e, poi, si considerano puntiformi le due astronavi (Nota: la loro eventuale contrazione è del tutto inutile).
Chiamiamo, perciò, A, B e C le linee di universo relative a questi tre punti. Infine, interpretiamo l’ipotesi di Bell relativa a “identici programmi di accelerazione” come condizioni essenziale per dire che le linee di universo di B e C sono traiettorie spaziotemporali PARALLELE ma NON INERZIALI.
Per esempio, nel sistema di riferimento in quiete, la linea di universo di C è perfettamente uguale a quella di B, ma è spostata verso le x crescenti di una quantità costante Δx.
Tutte le nostre costruzioni iniziano dal diagramma base di Fig. 1a, che rappresenta le linee di universo B e C, l’evento a in cui il segnale luminoso viene emesso da A, e gli eventi b e c relativi alla ricezione del segnale da B e C.
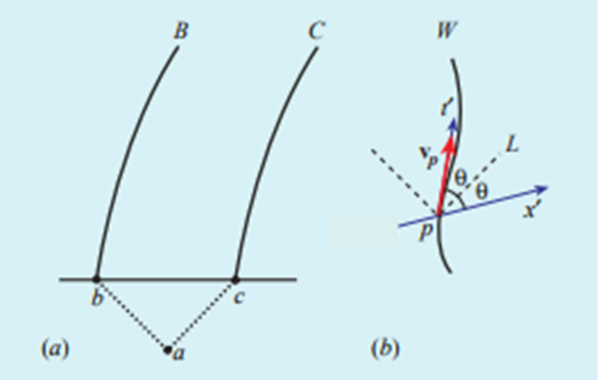
La nostra dimostrazione abbisogna spesso anche del tracciamento degli assi di un sistema inerziale K’, relativo a una particella la cui linea di universo è una linea di universo non inerziale (vedi Fig. 1b). Sia W un’arbitraria linea di universo non inerziale e sia p un evento che le appartiene. Sia vp il vettore tangente alla linea, che corrisponde alla velocità istantanea. L’asse t’ coincide, ovviamente, con la direzione di vp. L’asse x’ è l’asse di simultaneità di p. Per costruirlo facilmente, disegniamo il cono di luce L in p e misuriamo l’angolo θ tra vp ed L, e tracciamo una retta che passi per p e che sottenda un angolo θ rispetto a l, ma dall’altro lato. Questa linea è l’insieme degli eventi che sono simultanei con p, per un osservatore che si muova con velocità istantanea vp.
Mostriamo che l’asserzione (1) è VERA tracciando il diagramma spaziotemporale, dimostrando sia l’asserzione (1a) che (1b). Occupiamoci di (1a), partendo sempre dal diagramma di base di Fig.1a. Scegliamo un punto qualsiasi p di C e tracciamone il vettore tangente vp, come mostrato in Fig. 2a.
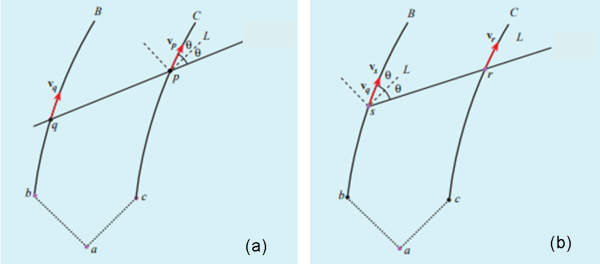
Tracciamo, ora, la linea di simultaneità relativa a p (Nota: come detto prima e come ben sappiamo dalle nostre lezioni sul diagramma di Minkowski) e il vettore tangente vq nel punto q dove la linea di simultaneità di p interseca la linea di universo B. Si nota subito che vq NON E’ PARALLELO a vp. In altre parole, OC giudica che in quell’ISTANTE la velocità di B sia minore di quella di C. Muovendosi lungo C, ossia facendo trascorrere il tempo proprio di OC, la linea di simultaneità del sistema inerziale in movimento si inclina ancora di più verso L, aumentando la differenza di velocità tra C e B. Ne segue che C giudica che B stia andando sempre più indietro, lontano da lui.
Basta ora usare un procedimento analogo per l’osservatore OB e si dimostra anche l’asserzione (1b). Si sceglie un punto arbitrario s su B, si costruisce la relativa linea di simultaneità, si trova il punto di intersezione r di questa linea con C e si confrontano vs e vr. In questo caso è immediato concludere che OB vede allontanarsi in avanti il corrispondente punto di C (Fig. 2b).
In entrambi i casi la corda si rompe a causa dello stress causatole dall’aumento della distanza tra le due astronavi, accertate da entrambe le astronavi.
Nota: la parte appena svolta è quella su cui ho sempre sorvolato, dato che la ritenevo la più ovvia e facile da comprendere.
Passiamo ora alle asserzioni (2) e (3).
Nota: teoricamente sembrerebbero le più facili, trattando il tutto da un sistema in quiete. In realtà, è così da un punto di vista “matematico”, ma, nel contempo, aprono le maggiori discordie da un punto di vista fisico. Quanto detto finora, infatti, non sembra ledere né la RR né la fisica dei materiali: una corda si rompe perché tirata sempre di più dai suoi due capi.
Iniziamo con il trasferire l’origine degli assi x e t, del sistema in quiete K, in modo tale da avere le due astronavi B e C lungo l’asse x. Prima della partenza le due astronavi corrispondono agli eventi b e c, come mostrato nella Fig. 3.
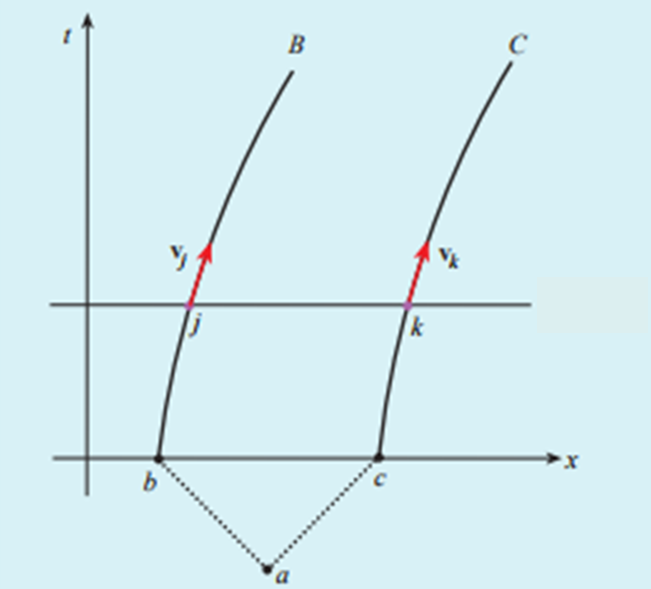
Scegliamo un punto arbitrario j su B e costruiamo la linea di simultaneità dell’osservatore in quiete OA che, ovviamente, è parallela a x. Tracciamo i vettori tangenti vj e vk, corrispondenti agli eventi j e k, in cui la linea di simultaneità di OA interseca le due linee di universo B e C. Si nota, immediatamente, che vj e vk sono paralleli. OA non può che giudicare che le due astronavi abbiano la stessa velocità in ogni istante. Di conseguenza, la loro distanza deve rimanere costante, durante tutta l’accelerazione e non solo, se misurata in K. (Nota: questo risultato è equivalente al dire che lo spazio tra le due astronavi non si contrae dato che appartiene a K, in quiete). L’asserzione (2) è dimostrata… ma, allora, perché la corda si rompe anche per OA?
OA ragiona in questo modo:
“La corda tesa copre esattamente la distanza tra B e C al tempo t = 0. Da quel momento in poi, la corda si muove in modo non inerziale, passando da un sistema “governato”* dal fattore di Lorentz a un altro, in cui ogni sistema successivo ha un valore più alto del fattore γ, che è funzione della velocità. (*Nota: nel lavoro originario si parla di “boosted-Lorentz frame”; boosted può essere tradotto come: una rappresentazione lineare che passa da un sistema di riferimento a un altro, nel quale ogni coordinata è aumentata o diminuita di un certo fattore. Un “boost” corrisponde a uno spostamento dell’intero sistema di coordinate senza alcuna rotazione degli assi).
Questa continua contrazione istantanea comporta un tensione nella corda. Per poterla mantenere costante sarebbe necessario che la distanza tra le due astronavi diminuisse continuamente. Tuttavia, questo non può succedere in K e, di conseguenza, le due astronavi esercitano sulla corda una certa forza crescente, fino a portarla alla rottura. Anche la (3) è dimostrata.
Nota: qualche parola in più su questa parte fondamentale… Non si parla di contrazione immediata, ma di una continua contrazione in un moto non inerziale, che permette l’introduzione di una forza che si oppone alla tensione della corda creata dalla contrazione istantanea. Questa è la parte sicuramente più delicata, che Bell tratta in modo estremamente complesso e dettagliato nel la suo lavoro originario. Nell’esempio semplificato che avevo proposto io si ammetteva “brutalmente” una contrazione immediata, dato che si ragionava solo con sistemi inerziali.
Tuttavia, Flores aggiunge una trattazione supplementare, estremamente interessante, anche se leggermente più complicata, che semplifica il tutto.
Possiamo costruire la linea di universo C* (in modo approssimativo), che l’astronave C dovrebbe percorrere per non rompere la corda, senza cambiare la linea di universo di B. Per poterlo fare, la distanza tra B e C deve rimanere costante nei successivi sistemi inerziali istantanei. Per costruire C*, per qualsiasi evento pi di B, si deve disegnare il sistema inerziale istantaneo K’, calibrare l’asse x’ e trovare l’evento ri, dove il capo superiore della corda dovrebbe trovarsi per non vedere aumentare la sua lunghezza. Dobbiamo tracciare una curva passante per gli eventi ri in modo da dare senso a C*. Confrontando C* con C, risulta chiaro che, se l’astronave seguisse C, causerebbe uno stiramento della corda che porterebbe alla sua rottura.
Entriamo nei dettagli della costruzione, in Fig. 4.
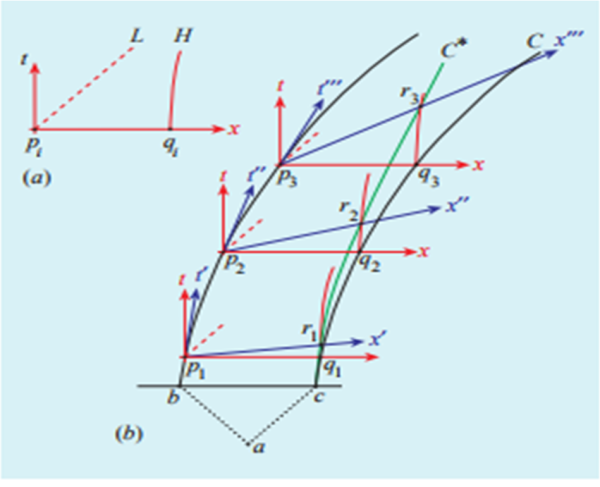
Cominciamo, come sempre, dal diagramma di base (Fig. 1a). In Fig. 4a disegniamo il cono di luce L nell’origine di K. Tracciamo, inoltre, l’iperbole H di calibrazione (vedi QUI) definita dall’invariante x2 – t2 = s2, dove s è la lunghezza della corda. Chiamiamo l’origine pi e l’intersezione di H con l’asse delle x, qi, in modo da anticipare il fatto che riproponiamo lo schema su tutto il diagramma di Fig. 4b, sia per il cono di luce che per l’iperbole (linee rosse). Imponendo che pi appartenga sempre a B, il corrispondente qi deve descrivere la curva C.
Il procedimento da seguire è piuttosto semplice. Per ogni pi, si disegna l’asse t’ (tangente alla curva B) e l’asse x’ di K’ (sistema inerziale istantaneo). L’intersezione di H con x’ viene chiamata ri. Poiché H è un INVARIANTE, dobbiamo avere x’2 – t’2 = s2. (Nota: l’iperbole non è altro che il luogo dei punti per il quale la distanza si mantiene al variare della velocità). Ne consegue che ri non è altro che l’estremo che la corda dovrebbe avere per mantenere una lunghezza costante s. La curva C* sarebbe proprio quella da seguire per passare per tutti gli eventi ri, capaci di mantenere costante la lunghezza del corda.
Infine, in Fig. 5, si possono disegnare le linee di simultaneità in K, che illustrano molto bene come per mantenere costante la lunghezza della corda, le astronavi devono muoversi in modo da diminuire costantemente la loro distanza, misurata in K.

Nota: Trovo questa trattazione (nell’impossibilità di seguire passo dopo passo quella di Bell) veramente geniale per dimostrare “per assurdo” che se l’astronave C mantenesse la stessa accelerazione di B, la corda dovrebbe per forza rompersi per la tensione! Anzi, io avrei direttamente affrontato la (3), introducendo subito la costruzione di C*. In poche parole, avrei detto: “Immaginiamo che la corda, malgrado le variazioni continue di velocità, si mantenga tesa senza alcuna tensione. Bene, perché questo succeda devo costruire, punto per punto, la distanza di una corda teorica di lunghezza costante. Questo si può fare facilmente utilizzando l’iperbole di calibrazione, punto per punto. Costruita la curva C* adatta allo scopo, si vedrebbe subito che non coincide con C e che deve costantemente avvicinarsi a quella di B. Ne segue che imponendo B e C come curve di base, la corda deve rompersi anche per il sistema in quiete”.
Le astronavi di Bell: pedagogia
Il valore pedagogico della distruzione del paradosso di Bell, attraverso semplici diagrammi spaziotemporali, sembra più che chiaro. Innanzitutto, perché gli studenti alle prime armi dovrebbero proprio limitarsi ai diagrammi. Inoltre, questo approccio non introduce assolutamente concetti più complicati come le nozioni di accelerazione propria, moto iperbolico e moto rigido. Solo entrando più a fondo nei problemi relativistici superiori è possibile ottenere direttamente una soluzione analitica di C*, assumendo, in particolare, un’accelerazione propria costante. Infine, questo approccio riesce, come voleva Bell, enfatizzare il fatto che, nella relatività, le leggi della fisica devono essere le stesse in tutti i sistemi inerziali. Infatti, tutti i sistemi inerziali coinvolti sono d’accordo sul fatto che la corda si deve rompere a seguito di una certa tensione.
Bibliografia: Bell J S 1993, How to teach special relativity Speakable and Unspeakable in Quantum Mechanics (Cambridge: Cambridge University Press) pp 67–80 (link).
Grazie Bell e grazie Flores per questa splendida lezione relativistica. Come studenti volenterosi vi siamo profondamente grati! Inoltre, ancora una volta, abbiamo capito che la semplicità vince sempre!






19 commenti
grazie
Ottimo "lavorone". Molto chiaro. Grazie !!!
Grazie per la traduzione, certamente utile per chi non conosce l'inglese.
In relativita ristretta, un “paradosso” si ha quando ci sono due punti di vista diversi, da parte di diversi osservatori inerziali in moto relativo, in merito ad un dato fenomeno fisico: siccome il fenomeno deve verificarsi alla stessa maniera nei due riferimenti, si deve trovare una soluzione unica, sulla base delle leggi relativistiche.
Nel caso delle astronavi e del filo , il paradosso nasce da qui :
1) secondo i piloti delle due astronavi, l'altra nave si allontana sempre più , e quindi il filo si rompe perchè è tirato fino a che si supera il carico di rottura
2) ma secondo l'osservatore terrestre, detto anche "di quiete" ( io preferisco: riferimento coordinato) , essendo uguali , in ogni istante di tempo terrestre, le accelerazioni e quindi le velocità , la distanza tra le navi non dovrebbe mutare, cioe dovrebbe rimanere uguale a quella che le navi avevano a terra prima della partenza. Percio il filo , steso ma non “teso” , non dovrebbe rompersi.
È il contrasto tra queste due opinioni, a costituire il paradosso! Allora, si tratta qui di far capire all'osservatore terrestre che sbaglia a pensare che la distanza tra le navi , che pure sono in moto rispetto a lui ( infatti, sono le navi portare a spasso il filo, questo non se ne va a zonzo per i fatti suoi) possa rimanere costante nel suo riferimento, sicché il filo non venga teso sempre di più, fino a rompersi !
E come si fa a convincerlo ? Per quanto mi riguarda, non certo invocando la “contrazione relativistica” , come dice Bell e ribadisce Flores . LA contrazione relativistica di un oggetto non induce, di per sè, uno stato tensionale nell'oggetto. LA parola "contrazione" è un modo infelice di indicare una misura della lunghezza di un oggetto in moto ridotta rispetto alla sua lunghezza propria .
Il filo subisce dei “boost” di Lorentz, passando da un sistema inerziale di quiete momentanea ad un altro , e cioè incrementando “leggermente” la velocita di volta in volta (questo non è un rigoroso linguaggio matematico, che comunque esiste) : ma i boost di Lorentz li subiscono anche le due navi , sono le due navi che portano a spasso il filo nello spazio, ripeto. Perciò , se il punto di vista dell'osservatore terrestre è che la lunghezza del filo , e la distanza delle navi, debba rimanere immutata per lui , bisogna fargli capire che in realta la “distanza fisica” tra le navi passa dal valore al valore
al valore 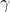
 , aumentata , non contratta , rispetto all'originale, e con aumenti crescenti , come è crescente il fattore
, aumentata , non contratta , rispetto all'originale, e con aumenti crescenti , come è crescente il fattore ) in funzione della velocita .
in funzione della velocita .
Dunque , non di contrazione relativistica si tratta qui, che sarebbe impedita da due navi la cui distanza rimane la stessa nel riferimento di quiete : perchè questa dicotomia ? LA navi e il filo si muovono insieme.
Si tratta piuttosto di “allungamento relativistico” continuamente crescente, carissimo Bell! Per cui alla fine, la contrazione di Lorentz , applicata alla quantita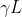 , riporta l'insieme “Nave A + cavo + Nave B” al valore
, riporta l'insieme “Nave A + cavo + Nave B” al valore 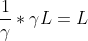 , e perciò l'osservatore terrestre può dire che la distanza , nel suo riferimento, rimane
, e perciò l'osservatore terrestre può dire che la distanza , nel suo riferimento, rimane  : questa lunghezza è in realtà la "contrazione globale di una misura allungata" . Spero sia chiaro.
: questa lunghezza è in realtà la "contrazione globale di una misura allungata" . Spero sia chiaro.
Quindi, anche l'osservatore terrestre deve ammettere che c'è una trazione del filo , e perciò la rottura ad un certo punto è inevitabile. La rottura è un fatto fisico inoppugnabile, e anche l'osservatore terrestre si deve arrendere al fatto che il filo viene tirato fino a rompersi, benche egli lo veda di lunghezza costante.
Ma so che non convincerò nessuno di questo. Non importa, ognuno rimane delle proprie idee . Nulla da dire , ovviamente, sulla spiegazione eccellente di Flores circa il punto di vista delle due navi.
Ho fatto altre ricerche; aggiungo ancora qualche link :
In questo link c'è la soluzione di David Morin, docente di Fisica ad Harvard:
https://www.physics.harvard.edu/uploads/files/undergrad/probweek/sol11.pdf
Come si vede , la soluzione si basa su questo semplice disegno , ed è originale :
Cioe, la nave A che sta dietro vede l'orologio di quella davanti B andare più in fretta del suo , di un fattore :
che si può ricavare con semplici considerazioni di meccanica classica : moto uniformemente accelerato, ma anche mediante ( addirittura!) il principio equivalenza e quindi la relatività generale, sia pure ad un livello molto elementare.
Altra soluzione è questa, presentata nel 2004 da due professori giapponesi :
http://studenci.fuw.edu.pl/~skfiz/stara/materialy/space_ships.pdf
a differenza dei precedenti autori, i giapponesi suppongono che la fase di accelerazione delle due navi sia brevissima , pressoché nulla ( visto che la variazione di velocità avviene in un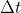
 ) , e perciò le due linee di universo dopo le accelerazioni sono parallele e rettilinee : sono le rette al di sopra dell'asse x , a partire da t=0, che quindi vogliono significare : velocità costante rispetto al riferimento coordinato .
) , e perciò le due linee di universo dopo le accelerazioni sono parallele e rettilinee : sono le rette al di sopra dell'asse x , a partire da t=0, che quindi vogliono significare : velocità costante rispetto al riferimento coordinato .
LA conclusione è la stessa, anche qui : la distanza tra le navi non è quella contratta , ma è quella aumentata rispetto a quella propria. Da energia presente che gli autori non parlano di filo ma di distanza tra le navi, almeno all'inizio. Essi propongono pure una soluzione general-relativistica , arrivando alla stessa formula proposta da Morin .
Ognuno ha il diritto disertare della propria opinione . Chiudo , saluti.
Correggo due refusi :
Errata : Da energia presente...(quartultimo rigo dal basso)
Corrige : Da tener presente ....
Errata :...disertare ....(ultimo rigo)
corrige : ...di restare...
Benissimo! Una chiara esposizione di una visione alternativa (nel sistema in quiete) è più che doverosa. Io resto dell'idea che siamo di fronte a visioni quasi filosofiche. Che un qualcosa si contragga o che venga tirata porta a una situazione praticamente identica. Ciò che dovrebbe essere ancora chiarito sarebbe l'intera trattazione di Bell, che ha avuto anche il conforto di Feynman. Fino a qui si è sempre girato attorno...Tuttavia, ci porterebbe troppo fuori del nostro livello e quindi ognuno la pensi come vuole... sapendo che le grandi conquiste lasciano sempre tante menti, più o meno elevate, a pensare e a ripensare, con motivazioni di tutti i tipi, a volte scientifiche a volte no...
Torniamo a cose più tranquille... , pensando al caro muone che, comunque, arriva FISICAMENTE sulla Terra solo perché la nostra atmosfera si è ristretta... Sarebbe bello chiedere a lui cosa ne pensa della contrazione di Lorentz... Chissà, un giorno...
, pensando al caro muone che, comunque, arriva FISICAMENTE sulla Terra solo perché la nostra atmosfera si è ristretta... Sarebbe bello chiedere a lui cosa ne pensa della contrazione di Lorentz... Chissà, un giorno... 
Garzie Enzo per questa utilissima esposizione dell'articolo di Flores e per le tue osservazioni che lo integrano. Ora penso che sia più semplice per tutti valutare i punti di vista dei vari autori che si sono cimentati con il problema.
Anche le argomentazioni di Pippo sono molto interessanti, come pure le impostazioni degli autori che cita.
Il dato di fatto che emerge prepotentemente è che, in ogni caso, la rottura avviene perché ad un certo istante la corda non è più in grado di assorbire la sollecitazione energetica a cui è sottoposta, che ha origine nella gestione dei motori dei razzi, ossia nella la dinamica dei punti che muovono le sua estremità.
Certo che se la programmazione dei motori, invece di essere fatta in base al tempo dell'osservatore in quiete ( tempo che coincide con quello dei razzi solo all'istante iniziale) , fosse stata fatta tenendo conto della diversità del fluire dei rispettivi tempi, la corda non avrebbe subito alcuno stress.
Eh sì, Maurizio... bastava seguire quanto detto dalla curva C*... bene a sapersi per il prossimo viaggio
Il muone ottiene un risultato incredibile, grazie alla contrazione di Lorentz. E' come se la distanza che attraversa si riducesse drasticamente, è come se il tempo della sua esistenza si allungasse a dismisura. La geometria varia in funzione delle condizioni fisiche in cui si svolge un fenomeno, così come le misurazioni su un piano non corrispondono a quelle su una superficie di altra natura immersa nello spazio. Sul tempo meglio non fare ragionamenti, dato che nei fatti non sappiamo di cosa si stia parlando.
Che il muone arrivi sulla terra, o la terra catturi il muone, il dato non illusorio è che si trovano nello stesso punto allo stesso istante, all'intersezione di due traiettorie che, inaspettatamente si incrociano.
Oppure i muoni "allevati a terra" non sono longevi per loro natura, come quelli selvaggi? La mia ignoranza mi fa chiedere: come siamo certi che i due tipi di particelle siano perfettamente equivalenti? In fondo sono nate in contesti diversi e hanno vissuto la loro, comunque breve, vita in condizioni disomogenee.
Temo, Mau, che si arrivi al sesso degli angeli... Perché un certo fotone DECIDE di entrare nel vetro e un altro torna indietro? I muoni astronauti sembrano proprio uguali a quelli di laboratorio... ma dovrebbero dircelo loro. Forse lo fanno, ma noi non li capiamo (è un po' come in tanti racconti di Astericcio & co...)
Grazie Enzo.
Saltano continuamente fuori nuovi aspetti della relatività. E' faticoso seguirli ma maledettamente stimolante.
grazie Fabry...
E un grazie anche a Pippo che ha mantenuto vivo l'argomento.
ovviamente...
Lo spazio attraverso cui si muovono i razzi e' fermo rispetto al sistema a riposo quindi non può contrarsi quindi la distanza non può variare
mentre la lunghezza della corda che si muove rispetto all osservatore fisso subisce la contrazione di Lorentz
Il muore vede lo spazio muoversi verso di lui quindi per lui lo spazio si contrae subendo la contrazione di Lorentz
L'osservatore a riposo non vede lo spazio contrarsi ma misura il tempo impiegato dal muore per decadere essere maggiore del tempo proprio misurato dal muone
Mi sono visto costretto a rimuovere alcuni commenti che inducevano in gravi errori di comprensione ed erano chiaramente inseriti per confondere le idee (facendomi dire proprio l'opposto di quello che ho cercato di spiegare finora). Lascio il commento di Fiore che è una perfetta sintesi di quanto abbiamo sempre detto. Ripetere non fa mai male... grazie Fiore!
Accedendo dopo qualche giorno al blog, vedo che la discussione è proseguita con grande partecipazione.
L'articolo di Flores mi è sembrato portare argomenti chiari e, per quanto possibile, semplici a favore della rottura della corda. Ma forse, in tutti gli interventi che ci sono stati nel circolo non si era messa in discussione questa conclusione. Quello che mi sembra sia stato più dibattuto, almeno da me, è la causa di questa rottura.
Negli interventi mi sembra si propenda ad inserire la contrazione di Lorentz tra le cause, almeno quando si vuole spiegare il fenomeno nel riferimento fermo. Ammetto che potrei rischiare di interpretare in modo errato gli interventi degli altri. Metto in forma dubitativa la mia asserzione.
Una eventuale attribuzione alla contrazione di Lorentz quale causa della rottura la vedo come una lettura distorta del fenomeno. Forse banalizzo, ma mi suona come se si dicesse "un pedone ha investito un auto". Nel riferimento dell'auto potrebbe essere una descrizione corretta, ma la frase ci suonerebbe comunque strana.
Flores anche nel riferimento fermo, che chiama K, spiega diversamente il fenomeno:
"..to keep the string taught, without changing the tension on the string, the distance between the spaceships as measured in K should decrease continuously. Since the distance between the spaceships in K remains constant, the spaceships are exerting a force on the string. Therefore, the string will break."
Certo, utilizza la contrazione di Lorentz per arrivare a questo, ma mi sembra la utilizzi nel ruolo di sintesi della trasformazione di coordinate. La causa l'attribuisce comunque alle forze esercitate dalle astronavi.
caro Fabry,
quando si discute la costruzione della curva C* si ottiene proprio questo. Tuttavia, come dici tu, la causa rimane la contrazione istantanea che si riflette sulle due astronavi che, mantenendo costante la loro distanza, esercitano una tensione.
mettiamola così, cambiando sistema, cambia non solo gamma, ma è come se l'oggetto in questione (la corda) cambiasse ogni volta: una serie di oggetti definiti da una serie di eventi sempre diversi. potremmo dire (con un po' di fantasia) che non è mi la stessa corda quella che subisce la tensione, ma una corda sempre più corta (vedi parte finale della soluzione della macchina e garage, parte seconda...).
Flores dice: per tenere la corda tesa, senza cambiargli la tensione, la distanza tra le navi dovrebbe cambiare e diminuire (curva C*). Siccome non lo fa, si origina una tensione da parte delle astronavi, ma, comunque, dato che le astronavi non possono cambiare distanza, l'unica cosa che può agire è l'accorciamento della corda (o se vuoi una "nuova" corda che ha la stessa realtà di quella di prima... La corda è una striscia di Universo che cambia forma a seconda da che sistema la guardi. Dato che non esiste un sistema assoluto, tutti hanno la stessa validità reale!
Di più non riesco a dire... nessuno pretende che sia la corda a tirare le astronavi, ma se la riduci, sono le astronavi che la tirano. Fissandone una, l'altra dovrebbe percorrere una traiettoria diversa. Cambiando corda è ovvio che succede questo.
Pensiamoci: per quale motivo la corda in quiete è diversa da una corda ristrettasi rispetto al sistema in quiete? Sono oggetti diversi che mantengono la loro validità fisica...
Volevo chiederle perché non scrive un articolo sui sistemi accelerati in RR
caro Fiore,
tu hai sicuramente ragione... anche se una trattazione accurata è abbastanza ostica. E' meglio rimandarla all'autunno, ma resta una buona idea! Intanto, potresti cominciare a raccogliere materiale e poi vediamo come agire...
Nel frattempo guarda sulla posta privata... c'è una sorpresina...