Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO nel quale è stato inserito anche il presente articolo

 

Mi sono accorto di non avere mai parlato espressamente dei metodi usati per la determinazione della velocità della luce. Devo colmare questo buco... Questa volta parliamo dei due metodi astronomici, la prossima volta dei metodi "terrestri".

Fin dai tempi più antichi ci si è sempre chiesti se la luce avesse una sua velocità o si propagasse istantaneamente. Sapendo, oggi, che essa si aggira intorno ai 300 000 km/s, risulta ovvio che nessuno avrebbe potuto rispondere, con le informazioni che si potevano ottenere sul nostro pianeta, troppo piccolo per permettere misure oltre ai limiti di una tecnologia ancora troppo rozza.

Il grande Galileo si era fatto quella domanda e aveva già intuito che la questione era ancora lontano dal potere essere risolta, dopo aver fatto tentativi ai limiti delle possibilità di quei tempi: orologi molto approssimativi e distanze troppo corte. Ne avevamo già parlato, ma ricordiamo, comunque, che aveva mandato un suo assistente su una collina piuttosto distante dalla sua, con una lampada in mano (o meglio torcia o qualcosa di simile). Galileo aveva acceso la sua torcia al tempo t₁, il suo assistente, una volta vista la luce, aveva mostrato la sua torcia (al tempo t₂) e infine Galileo aveva segnato il tempo t_3, in cui aveva ricevuto la luce dell’assistente. Malgrado avessero anche cercato di allungare il percorso con degli specchi, il risultato non poté che essere negativo.

Infatti, la velocità della luce avrebbe dovuta essere calcolata dividendo la doppia distanza 2d, tra Galileo e l’assistente,  per la differenza di tempo t₃ – t₁. Oggi ci viene da ridere, dato che t₃ – t₁ era troppo piccolo per essere misurato da orologi ancora primitivi (ma lo sarebbe tutt’ora) e quindi il risultato non poteva che essere : velocità infinta (d/0 => ∞)!

Tuttavia, Galileo aveva capito che il valore poteva benissimo essere finito, ma che per il momento non si poteva che accettare una velocità infinita, ossia assumere che la luce si propagasse in un tempo trascurabile a tutti gli effetti.

In altre parole, la Terra era troppo piccola per fornire distanze tali da accettare gli errori sui tempi e ottenere una velocità in qualche modo approssimata, ma sensata. Ci sarebbe voluto un assistente posto al di fuori del nostro pianeta o, quantomeno, un specchio molto, molto lontano, che inviasse indietro il raggio luminoso, permettendo che passasse un tempo, tra partenza e arrivo, abbastanza lungo.

Eppure, fu proprio Galileo a fornire la prima possibilità di misura della velocità della luce, attraverso la  scoperta dei satelliti medicei. Lui non ci pensò (probabilmente), ma aveva proprio “creato” la sorgente lontana, a distanza conosciuta, che poteva inviare il segnale luminoso!

I satelliti di Giove furono osservati a lungo negli anni successivi alla loro scoperta e così anche le eclissi dei suoi satelliti. Cassini eseguì osservazioni meravigliose a riguardo. Un astronomo olandese, Olaus Roemer, analizzò a lungo queste osservazioni e si accorse che qualche cosa non andava per il suo verso. Si poteva dire di conoscere abbastanza bene l’orbita terrestre e le orbite dei satelliti attorno a Giove e niente avrebbe potuto cambiarle (ipotesi più che valida per quei tempi). Ragione per cui l’ingresso dei satelliti nell’ombra di Giove, nelle varie configurazioni geometriche, doveva avvenire in istanti calcolabili abbastanza facilmente con la precisione degli orologi. E, invece, si trovavano differenze troppo elevate.

In particolare, più la Terra si avvicinava a Giove e più i tempi di ingresso nell’ombra anticipavano. L’esatto contrario, quando la Terra si allontanava (osservando, ad esempio, l’uscita dall’ombra). La Fig. 2 mostra bene la situazione per il satellite Io. Mentre la Terra passa da T1 a T2 gli ingressi anticipano; quando passa da T3 a T4 le uscite ritardano. Roemer, in realtà, valutava la durata dell’intera eclissi e trovava una sua durata variabile. Il succo del discorso è, però, esattamente lo stesso.

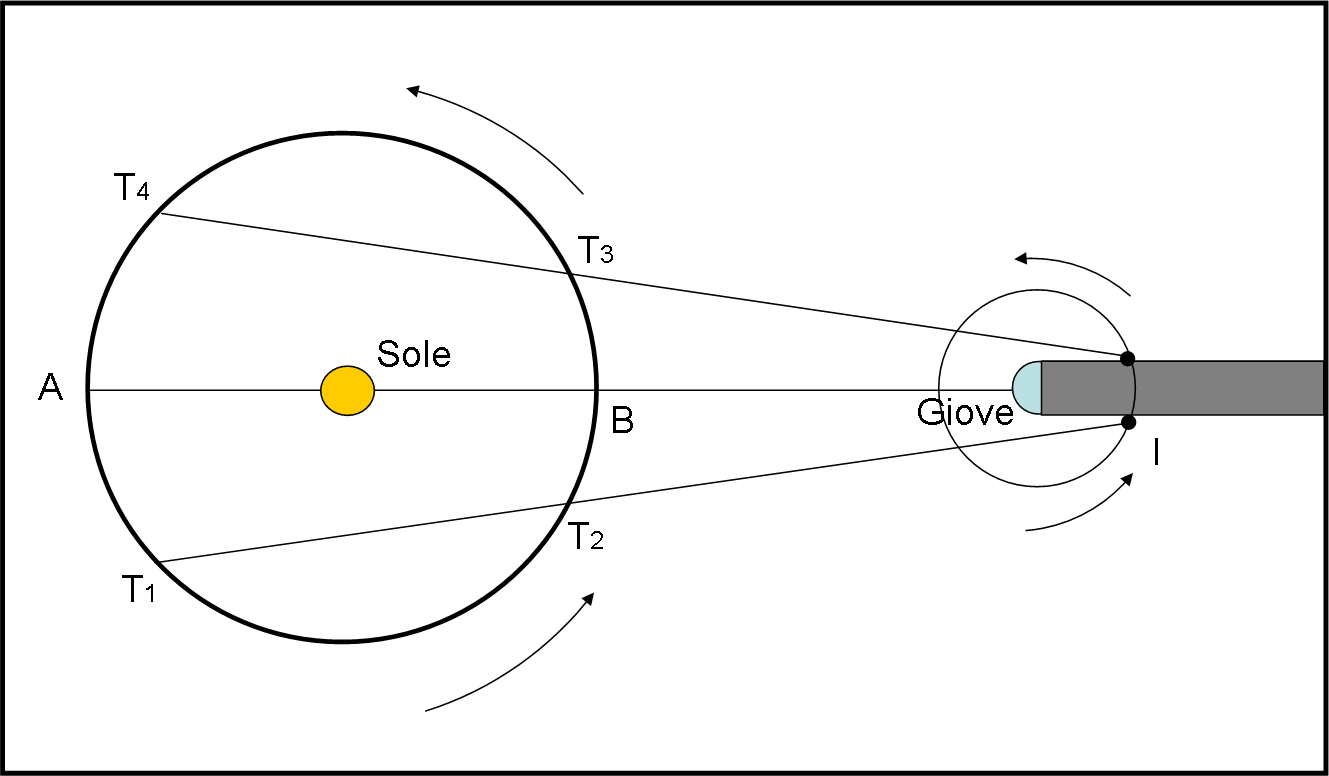
Come sempre, per le idee geniali, oggi sembrerebbe che ci volesse ben poco a capire che queste variazioni così regolari fossero dovute alla variazione della distanza tra la Terra e Giove o -meglio- alla distanza tra Io e la Terra, ma dobbiamo ricordare che molti colleghi scienziati di Roemer, anche prestigiosi, erano ancora convinti (seguendo Aristotele) che la luce dovesse propagarsi istantaneamente. I preconcetti sono duri a morire e certe conclusioni contro la credenza collettiva sono sempre atti di coraggio (rogo o non rogo).

Attraverso molte osservazioni, Roemer riuscì a riportare il problema a un semplicissimo schema, che introduceva le distanze di Giove misurata da A e da B e legava a loro le differenze di tempo tra due ingressi di Io nell’ombra. In semplicissime parole matematiche:

velocità luce = (A_I – B_I)/(t_A – t_B) = 2a/dt = c

Dove 2a è il diametro dell’orbita terrestre e dt la differenza di tempo massima calcolata attraverso molte osservazioni. La c che è stata associata alla velocità della luce viene dal latino “celeritas”.

Purtroppo, ai tempi di Roemer, la distanza Terra-Sole era conosciuta con grande imprecisione, così come vi era un errore ancora sensibile nella differenza dei tempi (dell'ordine dei venti minuti). Ne segue che il valore dedotto dal grande olandese nel 1676 fu di solo 210 000 km/s. Molto meno del valore reale, ma il concetto era giusto e a fine settecento si ottenne già un valore ben più preciso, pari a 310 000 km/s.

Galileo aveva ragione e la luce diventava una grandezza fisica a tutti gli effetti.

Non era ancora passato mezzo secolo dalla determinazione di Roemer, che Bradley, nella continua ricerca di misurare la parallasse stellare, si convinse di esserci riuscito, osservando la stella gamma del Dragone. Il valore trovato fu di 20.5”. Veramente grande… troppo grande (la stella sarebbe stata troppo vicina!). Ma, ancor peggio Bradley si accorse che anche le altre stelle mostravano la stessa parallasse annua. In poche parole non aveva misurato la parallasse, ma l’aberrazione annua, una scoperta estremamente importante per vari motivi.

Non voglio entrare nei dettagli, dato che l’abbiamo trattata molto attentamente in questo approfondimento.  Un approfondimento che è molto interessante non solo per la determinazione di c. In qualche modo, sto cercando di invogliarvi ad andare a rileggerlo, se non lo avete già fatto. Poi, quanto diremo di seguito, diventerà cosa più che banale.

Resta il fatto che l’angolo “apparente” sotto cui si vede una stella differisce da quello “vero” a causa della combinazione della direzione da cui proviene la luce e la direzione verso cui si sta muovendo la Terra nella sua orbita attorno al Sole. In altre parole, l’angolo dipende dal rapporto tra velocità della luce e velocità orbitale (La Fig. 2 riporta il concetto base dell’aberrazione).

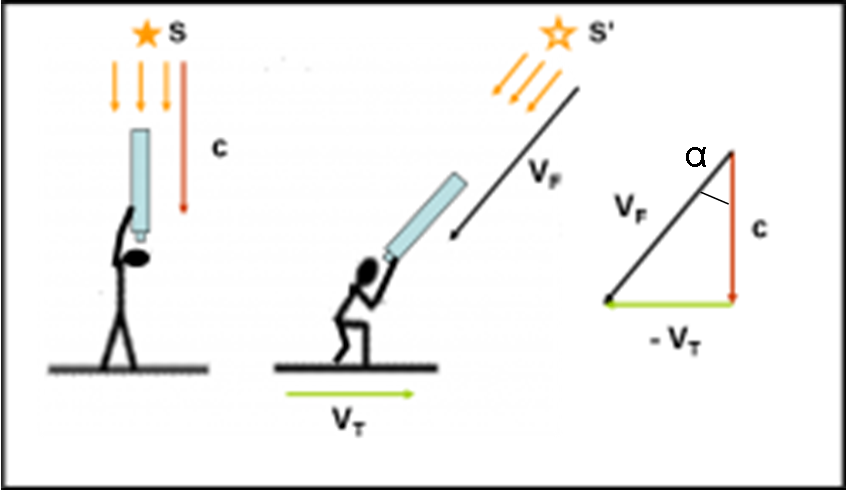
L’angolo α di aberrazione si misurava attraverso le osservazioni e la velocità della Terra era nota (30 km/sec). Ne seguiva immediatamente il valore di c, che risultò essere

c = 301 000 km/s

Una piccola-grande conseguenza dell’aberrazione annua, che riguarda più da vicino l’esperimento di Michelson e Morley (QUI in versione semplificata): se l’etere fosse stato a riposo rispetto alla Terra, esso si sarebbe mosso insieme a lei con la stessa velocità. Ma, in questo caso, anche il raggio di luce sarebbe stato trascinato insieme all’etere e l’aberrazione non avrebbe dovuto esistere. Questo fatto implicava, perciò, un etere fisso rispetto al moto del nostro pianeta e, di conseguenza, l’ipotesi di un vento dell’etere era più che accettabile.

 

E se la velocità della luce fosse diversa da quella che è? Ne abbiamo parlato QUI...

Questo articolo è stato inserito nella pagina d'archivio GIOVE E I SUOI TESORI, in SISTEMA SOLARE.