Gli altri articoli di questa serie (LA SFERA DI POINCARÉ) , li trovate nel'archivio--> Matematica e geometria-->Matematiche pure

La curvatura è un argomento che è stato più volte trattato in questo circolo dal punto di visto divulgativo. Vogliamo adesso approfondire tale concetto dal punto di vista formale, servendoci anche di quanto visto per le curve piane.

Introduzione.

Vogliamo ora definire uno strumento in grado di dirci qualcosa circa la curvatura di una superficie in un suo punto P. Ci sono due metodi per affrontare l’argomento, ed entrambi le strade portano alla stessa soluzione: la strada percorsa da Eulero fa uso della nozione di curvatura delle linee che giacciono su S (per calcolare la curvatura di una superficie in un suo punto P ci si riduce alla curvatura delle linee che giacciono su S e che passano per tale punto); la strada percorsa da Gauss sfrutta invece la variabilità della normale mediante l’immagine sferica della superficie costruita con da quella che è definita mappa di Gauss. Noi seguiamo la strada percorsa da Eulero. Attenzione a non confondersi: in realtà tale curvatura  di chiama curvatura gaussiana ma lo studio delle curvature principali fu fatto da Eulero.

Le curve nello spazio

Nell'articolo che trovate qui, abbiamo parlato di curve piane, del vettore velocità in tali curve, e quindi del vettore tangente. Tratteremo adesso gli stessi enti, ma nello spazio: le definizioni restano pressoché invariate, ma abbiamo fa che fare con equazioni parametriche a tre dimensioni:

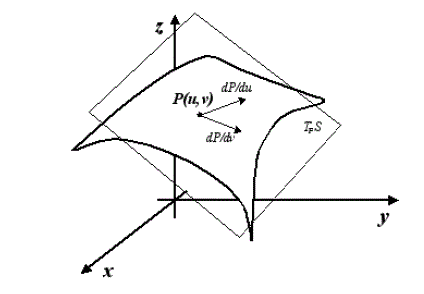
Il singolo punto avrà tre coordinate, P(t) = (x(t), y(t), z(t)) e di conseguenza anche il vettore velocità  v = dP (t) /dt= d x(t)/dt i + dy(t)/dt j + dz(t)/dt k, dove i,j, k sono i vettori base dello spazio tridimensionale Euclideo.

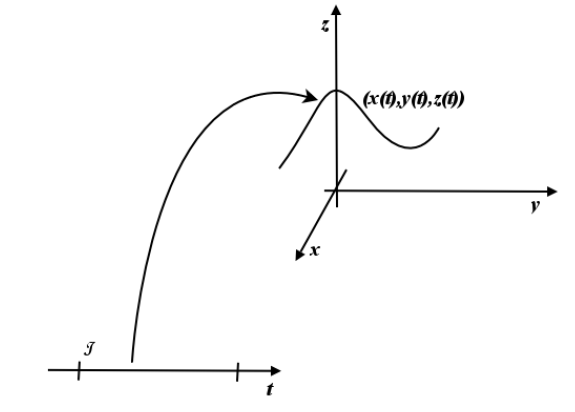
Nell'immagine, potete vedere una curva nello spazio tridimensionale; l'unico parametro è ancora t, ma le equazioni che la definiscono sono  tre. Anche la definizione del parametro arco resta la stessa; è l'integrale del vettore velocità che si ottiene lasciando libero l'estremo superiore, e rappresenta lo spazio percorso sulla curva al tempo t:

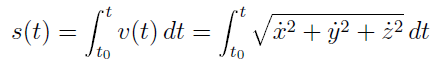
L'importanza della curva parametrizzata con il parametro arco , si rileva nella definizione stessa di curvatura,che abbiamo dato per le curve piane:

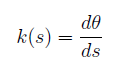Nel caso però di curve tridimensionali, la curvatura non può essere definita solo da uno scalare, ma  viene definita in modo vettoriale:

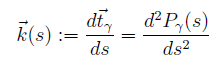dove t è il vettore tangente,  mentre la curvatura si ottiene calcando la velocità di variazione di tale vettore nello spazio.

Curvatura normale e curvatura gaussiana
Sia quindi P (s) il generico punto di una curva su  una superficie S parametrizzata con il suo parametro arco, calcolabile lasciando variare liberamente il secondo estremo nell ’ integrale che definisce tale parametro. Detto t il vettore tangente alla curva,  ha un vettore curvatura

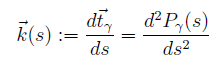
Il problema  è che, mentre nel caso di una curva nel piano, il vettore curvatura giace  esso stesso nel piano della curva, per una generica curva su una superficie, in generale, , ovvero il vettore curvatura in un punto non appartiene al piano tangente al punto.

L’idea è  che la componente tangenziale di questo vettore sia propria della curva, mentre la parte normale di questo
vettore sia dovuta alla superficie, e dunque manifestazione della curvatura della superficie.

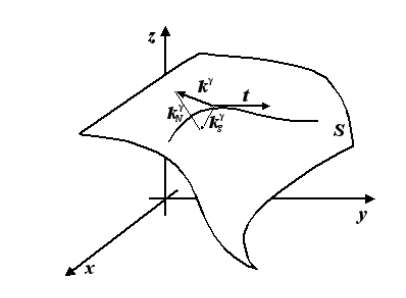
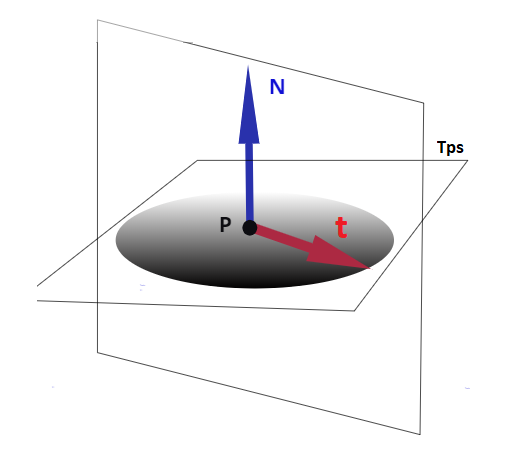
Nel disegno:t è il vettore tangente alla curva contenuta nella superficie S; è il vettore curvatura che si ottiene derivando t rispetto al parametro arco, ovvero dalla definizione di  curvatura di una curva nello spazio;   è la componente di tangente alla superficie (chiamato vettore di curvatura geodetica, o vettore di curvatura tangenziale), mentre è la componente di  ortogonale alla superficie, chiamato vettore di curvatura normale Entrambi ovviamente dipendono dalla curva γ(s), e dal valore di s.

Per questo introduciamo la seguente definizione:

Si chiama curvatura normale di una curva giacente su S e passante per P, la componente normale del vettore curvatura di in P. In simboli:

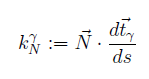
(ovviamente per trovare la componente normale, basta fare il prodotto scalare fra  il vettore curvatura e la normale alla superficie).

La curvatura normale in un punto dipende  dalla curva  che scelgo passare per tale punto.

Si chiama invece  curvatura geodetica di una curva giacente su S e passante per P, la componente tangente del vettore curvatura di in P.

Tra tutte le curve passanti per un punto, ce ne sono alcune che hanno una proprietà particolare, quella di essere ottenute mediante l’intersezione della superficie con un piano ad essa normale.
 Si chiama sezione normale la sezione di S ottenuta tagliando S con un piano ad essa normale.

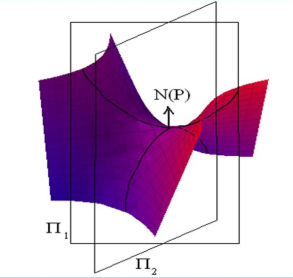
Sostanzialmente, in ogni punto P è  definito il versore N perpendicolare alla superficie.Tale vettore altro non è che il versore normale al piano tangente alla superficie nel punto P, che esiste perchè la varietà è differenziabile. Per tale direzione passa un fascio di piani, detti sezioni normali. L'intersezione della superficie con la sezione determina una curva;presa una curva qualsiasi con un certo versore tangente t, la sua curvatura normale Kn sarà uguale alla curvatura normale della sezione normale avente lo stesso versore tangente t. In parole povere dipende solo da t, e non dalla particolare curva tangente a t.

La curvatura normale è quindi una funzione (continua) definita sulla circonferenza unitaria S1 che giace nel piano tangente:

f: S1--->R

a ogni direzione in questa circonferenza è associato un valore di Kn. Essendo la circonferenza unitaria S1 un compatto, per il Teorema di Weierstrass, Kn ammette massimo e minimo in S1. Sia Kmax il massimo e Kmin il minimo.

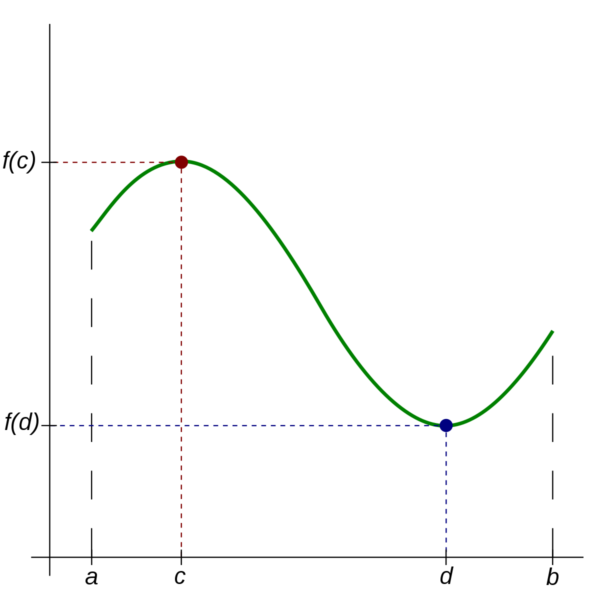
Questi valori, ossia la curvatura massima e minima al variare della sezione normale, sono detti curvature principali.

Si chiama curvatura gaussiana K della superficie S  in un suo punto P il prodotto delle curvature principali:
K = Kmin · Kmax

Quanto vale la curvatura gaussiana del cilindro? e quella del cono?
Contrariamente all'intuizione, queste superfici non sono affatto curve! Infatti in ogni punto possiamo individuare una sezione di curvatura minima (zero) che corrisponde ad una retta, pertanto la curvatura gaussiana, essendo il prodotto delle curvature principali, sarà nulla. Questo dipende dal fatto che se incurviamo senza distorsione un foglio di carta piatto, formando un cilindro o un cono, sia il cilindro sia il cono hanno la stessa geometria intrinseca del foglio piatto, sebbene le loro geometrie estrinseche siano del tutto diverse.

(spero cosa si intenda per intrinseco ed estrinseco; basta il significato letterale. Chiariremo poi dal punto di vista geometrico cosa significa in dettaglio).

Quanto vale la curvatura della sfera?

Nel caso di una superficie sferica di raggio r si ha invece che tutte le sezioni normali, per qualsiasi punto P, sono uguali; sono infatti circonferenze massime di curvatura 1/r (tenete presente che il piano tangente è perpendicolare al raggio della sfera per P, quindi la normale n passa per il centro della sfera); ne segue che la curvatura della superficie è ovunque uguale a 1/r² ed è sempre positiva. La superficie sferica ha curvatura costante positiva.

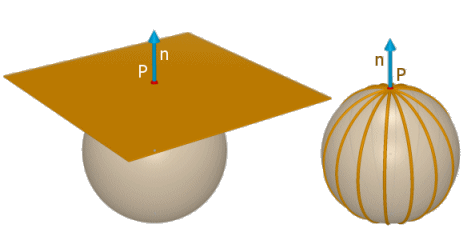
La curvatura è una proprietà intrinseca.

Abbiamo introdotto le varietà differenziabili, sfruttando la definizione di varietà immersa in uno spazio di dimensione superiore. Nel caso delle superfici.

Ricordiamo come viene definita  una superficie( o meglio un elemento di superficie) in :

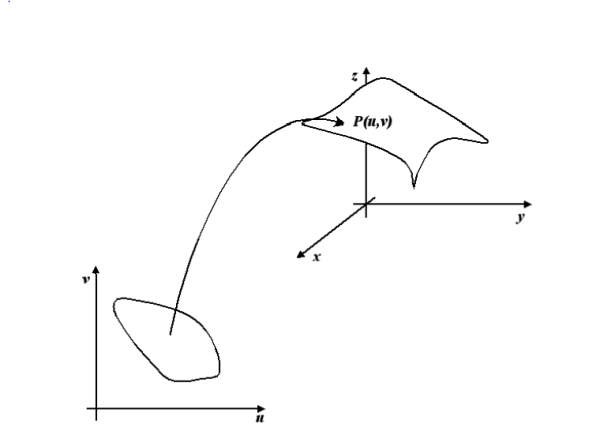
Ricordando  la topologia, possiamo parlare di carte,  ossia di omeomorfismi  fra un aperto del piano e un aperto dello  spazio .  Visto che abbiamo a che fare con aperti dello spazio euclideo, possiamo esplicitare facilmente questi omeomorfismi,  che indichiamo con :

usando ad esempio delle funzioni parametriche:

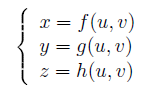
che dipendono appunto dai parametri u.v.Ci verrebbe ora in mente la malsana idea di calcolare la curvatura di una superficie usando uno dei metodi esposti in questo paragrafo applicati alle equazioni parametriche. Andremmo incontro a calcoli di una difficoltà mostruosa, per alla fine avere in più che giustificato dubbio; ma e se la curvatura dipendesse dalle equazioni parametriche    scelte per rappresentare la superficie, cosa avremmo concluso? Bè , proprio un bel niente. Per fortuna ci viene in aiuto Gauss con il suo teorema più famoso, che chiamò proprio così per la sua importanza:

Teorema egregium (di Gauss)

Il teorema egregium  è un risultato di geometria differenziale che afferma che la curvatura gaussiana K è una grandezza intrinseca di una superficie,ovvero non dipende dal'immersione. Anzi, e questo esempio fu scoperto più avanti da Poincarè, esistono superfici che non sono rappresentabili tramite immersione.  Eravamo  nel 1827.. ma questo era un risultato di un importanza cruciale per il futuro, grazie all'estensione da parte di Riemann alle varietà di dimensione qualsiasi. Ma se la curvatura è una grandezza intrinseca, degli esseri (bidimensionali nel caso delle superfici) come fanno a rendersi conto di non essere in uno spazio piatto? La risposta fu data da Riemann: tramite la geometria. Gli basterebbe infatti disegnare un triangolo per rendersi conto che se non si è in una superficie piana, ossia a curvatura zero, la somma degli angoli interni non è 180°.

Per parlare però di geometria intrinseca, dobbiamo però avere a disposizione una curvatura costante in ogni punto della superficie. Se la curvatura non fosse uguale per tutti i punti, le figure geometriche subirebbero deformazioni in seguito a semplici traslazioni, e dunque i punti dello spazio non sarebbero equivalenti tra loro, cioè lo spazio non sarebbe omogeneo. Nel 1854 Riemann ha determinato il tipo di geometria in funzione della curvatura: è euclidea se la curvatura è nulla, sferica se la curvatura è positiva, iperbolica se la curvatura è negativa.

La geometria Euclidea la conosciamo; che proprietà hanno la geometria sferica e quella iperbolica?

La geometria sferica
Sulle superfici con curvatura positiva e costante viene definita una geometria sferica. Ecco le principali proprietà:
- per un punto esterno ad una retta data non passa alcuna retta parallela ad essa
- la somma degli angoli interni di un triangolo è maggiore di p-greco radianti
- il rapporto tra circonferenza e raggio è minore di 2(p-greco)
- l'estensione della superficie è finita

La geometria iperbolica
Sulle superfici a curvatura negativa e costante viene definita una geometria iperbolica. Ecco le principali proprietà:
- per un punto esterno ad una retta data si possono tracciare infinite rette parallele ad essa
- la somma degli angoli interni di un triangolo è minore di p-greco radianti
- il rapporto tra circonferenza e raggio è maggiore di 2(p-greco)
- l'estensione della superficie è infinita
Sembrerebbe impossibile rappresentare la pseudosfera in una porzione di piano, a causa della finitezza di quest'ultima regione. Invece esistono diverse rappresentazioni, la più interessante è quella di Poincaré perché è conforme, cioè conserva gli angoli e la forma delle figure geometriche. e il cui centro coincide con il centro della sfera.

Possiamo estendere questi discorsi ad una varietà di dimensione maggiore di 2, ovvero per esempio ad n=3, per tali motivi si dice spesso che lo spazio (tridimensionale) possa essere "curvo", ovvero possa avere una curvatura non nulla.

Di cosa parleremo nel prossimo articolo?

Abbiamo visto che nel caso delle curve piane, per definire la curvatura basta un numero. Nel caso generale, si può parlare di curvatura media, se abbiamo solo un valore per definirla. In realtà non basta un  numero, per definire la curvatura dello spazio ci vogliono ben sei numeri, che vanno a definire il tensore di Riemann. Il calcolo tensoriale rappresenta però il più grande scoglio presente nello studio quantitativo delle Relatività generale; perfino  Einstein si rivolse al suo amico Marcel Grossmann per risparmiarsi un bel pò della letteratura necessaria per poterci lavorare. Einstein si rivolse poi al nostro Ricci per risolvere le equazioni della R.G. Io volevo fare solo un cenno al concetto di tensore, e applicarlo al tensore di curvatura, ma capirete che non è impresa facile. Comunque possiamo provarci.

 

 

Gli altri articoli di questa serie:

0) Un progetto ambizioso

1. LE OMOTOPIE E LA SEMPLICE CONNESSIONE
2. L'ENUNCIATO DELLA CONGETTURA.
3. Le TRI-Varietà topologiche
4. Le varietà differenziabili
5. le varietà Riemmane-Introduzione
6. Le varieta-Riemmane
7. La curvatura in una curva piana