Categorie: Matematica Meccanica Celeste Strumenti e missioni
Tags: curve di Lissajous orbite di Lissajous orbite di Lyapunov orbite halo Punti Lagrangiani
Scritto da: Vincenzo Zappalà
Commenti:6
Siamo le curve più belle del mondo. 3 **
Questo articolo è inserito nelle sezioni d'archivio "Matematica e Geometria" e "Meccanica celeste"
Concludiamo (per adesso, almeno) la nostra visita alle curve di Lissajous, analizzando in modo molto semplificato la loro applicazione naturale e artificiale, nel campo "terribile" della Meccanica Celeste.
Lo avevamo già accennato (QUI e QUI): le curve di Lissajous piacciono molto all'Universo e possono essere considerate come una specie di luogo di pace e tranquillità nella frenesia dinamica del problema dei tre corpi. Abbiamo anche scoperto, attraverso le splendide foto del nostro amico Gilberto, come la Natura ami renderle vive attraverso le sue meravigliose creature marine.
Facciamo un piccolo salto e immergiamoci in un sistema composto da due grandi masse in rotazione attorno al proprio baricentro. Una situazione comunissima nell'Universo che resta, comunque, uno dei grandi problemi irrisolti da un punto di vista matematico. Cosa succede, infatti, a un terzo corpo, anche supposto avere una massa trascurabile, che venga inserito in questo sistema? Di tutto e di più, ma soprattutto niente che possa essere risolto analiticamente.
In quello spazio che sembra perfetto per stabilire una soluzione geometrica e fisica descrivibile completamente, il moto del terzo, piccolo, corpo, non è assolutamente prevedibile per via analitica. Su di esso agiscono le attrazioni gravitazionali dei due oggetti principali, la forza centrifuga e, se assumiamo un movimento del terzo corpo, anche la forza di Coriolis. E siamo ancora nel caso molto particolare di massa trascurabile e orbite circolari... Proviamo a inserire anche le perturbazioni dei pianeti, ad esempio, è la problematica diventa mostruosamente difficile.
Tuttavia, nel caso più semplificato, ricordiamo bene che Lagrange (anzi De La Grangia), ha trovato 5 punti di equilibrio (due stabili e tre instabili) in cui il terzo corpo di massa trascurabile può rintanarsi per riuscire a non sentire alcuno "stress" apparente e ruotare senza problemi in perfetta sincronia con le due masse dominanti. In poche parole, in questi punti tutto il sistema appare fermo e i due giganti sembrano immobili nel cielo. Vale la pena richiamarli: L1, L2 e L3 sono i punti instabili e posti a varie distanze lungo la congiungente le due masse principali. sia internamente che esternamente a loro, L4 e L5 sono i punti stabili, dove la situazione è la stessa, ma si trovano in posizione tale da formare un triangolo equilatero con i due corpi principali.
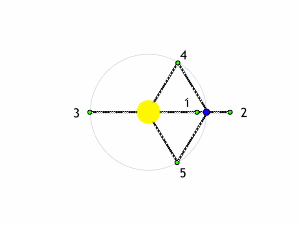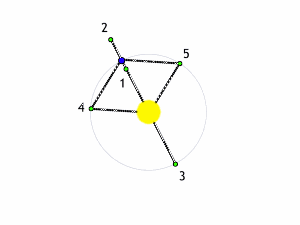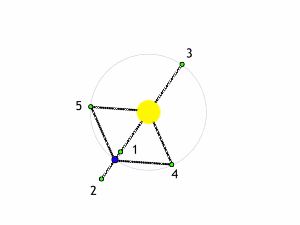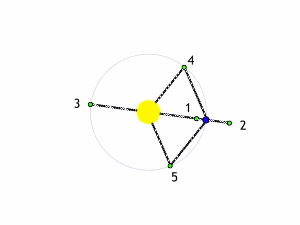
Ricordiamo, anche, che punti di equilibrio instabile sono quelli in cui un leggerissimo spostamento porta il terzo corpo a uscire dall'equilibrio, mentre nell'equilibrio stabile, il terzo corpo tende a riprendere la posizione iniziale. Su questa problematica potete trovare molti articoli di approfondimento, tra cui questo e questo.
Una situazione solo e soltanto teorica, un rifugio di tranquillità esistente solo sulla carta? No, in realtà nei pressi dei punti lagrangiani L4 e L5, tra i Sole e Giove, esiste un numero enorme di asteroidi che hanno trovato in quelle posizioni di grande stabilità un rifugio perfetto per non essere sbattuti chissà dove dall'azione perturbatrice di Giove. Questo non capita solo per i punti lagrangiani tra Sole e Giove, ma su scale ridotte, anche tra il Sole e altri pianeti e, addirittura, tra i pianeta e i suoi satelliti. Insomma, alla Natura, piacciono i punti lagrangiani, soprattutto se sono stabili.
Affrontiamo ora un discorso dall'apparenza quasi assurda, ma di estrema importanza non solo per l'Universo, ma anche per l'uomo(finché ce ne sarà qualcuno...) che cerca di imparare da lui e dalle sue leggi. Per potere effettuare un'orbita è necessario che vi sia una certa massa che "getti" la propria rete gravitazionale, sia intesa come un campo di forze newtoniano, sia intesa come una curvatura dello spaziotempo einsteniano. In poche parole, si può orbitare solo e soltanto attorno a una massa. E' vero che, in realtà, si ruota attorno al baricentro del sistema che è un punto fittizio, ma il baricentro rappresenta perfettamente il luogo, praticamente reale, in cui le due masse possono essere concentrate (perdonate la estrema semplificazione del problema). Ben diverso è il concetto di punto che esiste solo e soltanto come luogo di equilibrio tra forze completamente diverse (gravitazionale, centrifuga, di Coriolis)... in poche parole un punto lagrangiano.
Ebbene, la Natura è riuscita a mostrarci che si può benissimo orbitare attorno a uno di questi punti, anche se essi non esistono praticamente. L'homo veramente sapiens l'ha capito e ha saputo sfruttare questa "stranezza" dell'Universo per poterlo studiare meglio... Proprio in queste orbite ha inserito molti dei suoi preziosi "collaboratori" tecnologici spaziali
Andiamo avanti con calma...
Entriamo nel piano orbitale delle due masse principali. Possiamo tranquillamente considerare anche la Terra e la Luna. Identifichiamo abbastanza facilmente i tre punti lagrangiani L1, L2 e L3 (L4 e L5 servono molto meno per scopi "pratici"). Bene, attorno ad essi esistono delle orbite che si mantengono complanari con il sistema dei due corpi primari. Esse sono state trattate da Lyapunov e portano il suo nome. Attenzione: quando parliamo di orbite non parliamo veramente di traiettorie ellittiche, ma di traiettorie che si chiudono attorno a un punto lagrangiano ... non concreto. Nella figura che segue, vediamo una traiettoria di Lyapunov. Teoricamente questo tipo di orbita può anche svolgersi su un piano perpendicolare al piano orbitale dei due corpi principali.
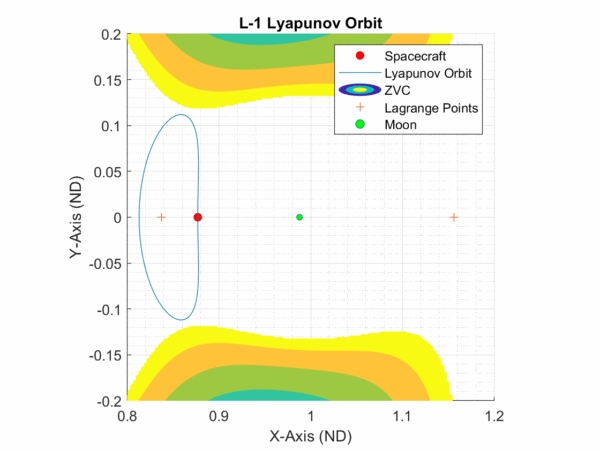
Maggiore importanza da un un punto di vista astrodinamico, per le loro effettive applicazioni, le hanno le orbite di tipo "halo". Esse sono sempre periodiche, ma si svolgono su piani inclinati rispetto a quello orbitale principale. Un esempio di inserimento di un telescopio in tale posizione è stato quello solare SOHO che orbita attorno al punto L1 tra Terra e Sole. Nelle figure che seguono ne vediamo l'inserimento e l'orbita, con vista polare ed equatoriale.

Ci siamo perfettamente capiti... queste strane orbite attorno ai punti lagrangiani instabili sono perfette per potervi posizionare dei telescopi che da un lato abbiano le giuste condizioni di visibilità specifiche per la missione (sempre in vista del Sole, sempre nascoste dalla luce solare, e via dicendo) e dall'altra che non abbiano bisogno di molto carburante per restare sempre nelle posizioni scelte. Al più hanno bisogno di piccole correzioni di tanto in tanto, soprattutto per tenere conto delle perturbazioni dovute agli altri pianeti. La stessa più o meno grande distanza rispetto ai punti lagrangiani può essere di grande utilità per cambiare la prospettiva di vista dello strumento.
Scendendo nei particolari più tecnici, notiamo che l'utilizzo dei punti di equilibrio L1 e L2 è utile per missioni scientifiche e di telecomunicazione. La posizione intorno al punto L2 del sistema Sole-Terra è caratterizzata da un ambiente termico stabile e da minime regioni di ombra terrestre o lunare. Invece, un satellite posto su un’orbita intorno a L1 del sistema Sole-Terra è continuamente illuminato dal Sole e mantiene una distanza quasi costante dalla Terra favorendo le comunicazioni. Le missioni di studio delle particelle e dei campi magnetici ed elettrici intorno alla Terra e alla Luna trovano nel primo e secondo punto collineare del sistema Terra-Luna le posizioni migliori. Inoltre, le orbite periodiche intorno a tali punti ,caratterizzate da grande escursione fuori dal piano di moto dei primari, sono ideali per l’osservazione delle regioni polari di entrambi i primari.
A noi, però, interessano specialmente altri tipi di orbite che, a prima vista, sembrerebbero meno controllabili e che, invece, vengono usate con grande frequenza. Il loro nome è tutto un programma: orbite di Lissajous. Simili a quelle "halo" (che possono essere considerati dei casi particolari), esse non sono periodiche, ma aperte... proprio come le curve di Lissajous ottenute con angoli il cui rapporto è irrazionale. Le sonde che le sfruttano descrivono proprio le curve più belle del mondo e sembrano dipingere nello spazio quadri astratti estremamente affascinanti. GAIA, ad esempio, le percorre attorno al punto L2 tra Terra e Sole.
Nello stesso punto sarà mandato il nuovo telescopio spaziale Webb.
Sempre nel punto L2 con il Sole è stata inserita la sonda WMAP per lo studio delle microonde. Nella figura che segue vediamo la sua immissione in orbita e la spettacolare curva di Lissajous che descrive.
Le missioni THEMIS/ARTEMIS, composte da varie navicelle spaziali per lo studio del campo magnetico terrestre e le interazioni con la Luna, si muovono sia in L1 che in L2 con la Luna, anche se solo per limitati periodi di tempo. Il filmato che segue mostra le orbite in un sistema che vede ruotare il sistema Terra-Luna
mentre la figura che segue si riferisce a una visione nel sistema rotante centrato sulla Luna.
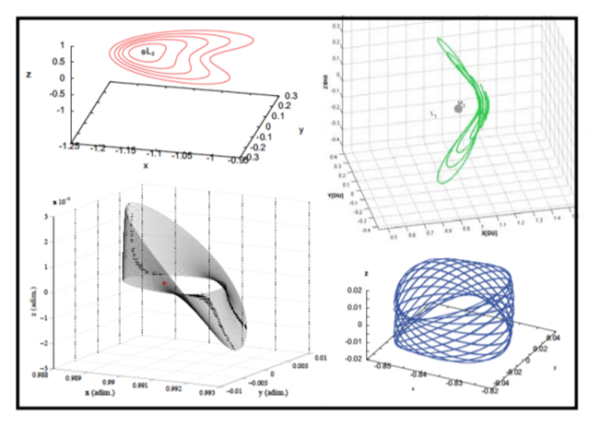
Un riassunto complessivo dei quattro tipi di curve sono riportati nella figura che segue, tratta dalla tesi di ingegneria aerospaziale sulle orbite di Lyapunov di Chiara Finocchietti
Per avere un quadro completo delle missioni passate e in atto attorno ai punti lagrangiani del Sistema Solare, insieme a quelle degli oggetti naturali, consiglio vivamente questa pagina
E' interessante notare come ciò che utilizza l'uomo non fa che imitare e cercare di estendere le applicazioni naturali di asteroidi e altri oggetti minori. Un passaggio di consegne tra la Natura e la capacità riflessiva dell'uomo "vero" e razionale. In questa comunione d'intenti e in questa reciproca comprensione le curve di Lissajous acquistano un valore molto particolare che va ben oltre la loro bellezza e importanza astrodinamica...
Fine (per adesso, almeno)









6 commenti
Vedo anche che volano a velocità piuttosto basse, di poche centinaia di km/h. Ciò significa che la forza di attrazione di questi punti è debole?
Non mi sono chiare inoltre le distanze in km che immagino si riferiscano alla Terra per Soho e alla Luna per Themis/Artemis. Mi piacerebbe capire invece quanto è circa lungo l"asse maggiore di queste orbite.
Cioè le osservazioni di questi satelliti, che io immaginavo perfettamente immobili, non risentono così di errori di parallasse?
Credo ci sia un refuso in: "GAIA, ad esempio, le percorre attorno al punto L2 tra Terra e Sole." Si tratta di L1, vero?
Caro Albertone, tali traiettorie sono ben conosciute e si può valutare esattamente la posizione del telescopio. Per sapere la loro ampiezza... basta avere un po' di pazienza e bloccare al momento giusto i filmati
Ce ne sono moltissime e, in fondo, anche Hubble si trovava sempre in una posizione diversa, rivolvendo attorno a noi...
No, no... è proprio L2. Perché... non ti piace?
Tra Terra e Sole c'è L1, mi pare che tu mi abbia insegnato. L2 sta dalla parte opposta, verso l'orbita di Marte