Il ritorno di Samatha Cristoforetti sulla Stazione spaziale internazionale ha acceso i riflettori mediatici su questo laboratorio che da oltre venti anni vola a circa 400 km sopra le nostre teste, compiendo un giro completo della Terra ogni circa 90 minuti. Perché, dunque, non riproporre alcuni articoli sul tema? Ma, in sintonia con lo stile di questo blog, non vi troverete l'elogio della (pur strabiliante) tecnologia, bensì un'occasione per rispolverare qualche semplicissimo concetto di geometria e trigonometria.

 

L'articolo che segue è un condensato di due articoli già pubblicati in questo blog: Quanta Terra si vede? e La stazione

 

Quanta Terra si vede?

(Vincenzo Zappalà - 23/11/2019)

Poniamoci una domanda... cosa vediamo se ci portiamo su una collina isolata di un centinaio di metri d'altezza? Se non ci fosse l'atmosfera  (cielo perfettamente terso) riusciremmo a vedere cose che distano circa 35 km da noi. Perché? Perché la Terra è una sfera e non un disco piatto. Potremmo, però, dire di vedere il bordo della sfera terrestre? Assolutamente no! Ciò che limita la vista è quello che si chiama orizzonte. Diamone una definizione precisa: la linea, mobile e dinamica, che divide la Terra dal cielo. Essa è, ovviamente, una circonferenza e su questo tutti possono essere d'accordo.

Immaginiamo adesso di alzarci in volo su un aereo transcontinentale e di viaggiare a 10 000 metri d'altezza. Beh... c'è una bella differenza! Adesso l'orizzonte continua a essere una circonferenza, ma ha un raggio di circa 356 km. Un bel passo in avanti, ma ancora una volta, potremmo dire di vedere i bordi della sfera terrestre? Assolutamente no. Comunque, abbiamo avuto un incremento del raggio pari a circa un fattore 10 rispetto alla collinetta di prima.

Cosa succederebbe se fossimo un astronauta e ci potessimo imbarcare sulla Stazione Spaziale? Bene... arriveremmo a 400 km dal suolo e il nostro orizzonte si amplierebbe sicuramente. Di quanto? Di una fattore 6. Accidenti! Così poco? Eh sì, un minimo calcolo geometrico ce lo conferma: il raggio del cerchio visibile diventa 2170 km. Potremmo, finalmente, dire che stiamo vedendo i confini della sfera terrestre? Ancora una volta, assolutamente no. Vediamo solo una parte maggiore della superficie terrestre, ma ben lontana dalla sua superficie totale. Per essere più o meno precisi vedremmo solo il 12% scarso della superficie totale visibile (una semisfera)

Possiamo perciò asserire, senza nessun rischio di commettere errori, che le splendide immagini prese dalla Stazione Spaziale, in cui si vede una bella linea curva che separa la terra dal cielo è ancora solo e soltanto un orizzonte, un po' più lontano di quanto abbiamo visto dall'aereo. Certamente non voi... ma chissà quanti sono convinti che quella linea curva sia veramente il bordo della superficie terrestre! Guardiamo l'immagine che segue e riflettiamo...

Bellissima, senza dubbio, ma quella curva che separa la terra dal cielo non è assolutamente il bordo della Terra.

Per poterlo vedere dovremmo andare molto, molto più lontano. Gli unici uomini che ci sono andati molto vicini sono gli astronauti che hanno raggiunto la Luna o le hanno orbitato attorno. Facciamo un po' di calcoli anche in questo caso... e troviamo che l'orizzonte della Terra visto dalla Luna  ha un raggio che è solo 1 km minore del suo raggio reale. Beh... in questo caso possiamo proprio dire che stiamo vedendo la semisfera terrestre nella sua interezza.

Ho voluto scherzare e, forse, smitizzare un po' il panorama che vedono la Cristoforetti e i suoi amici. In ogni modo è decisamente maggiore il salto che si compie dalla pianura a un aereo di linea che non quello tra l'aereo e la stazione spaziale. E questo anche se si parla di superficie visibile. Infatti quella osservata da 100 metri è pari a π35², mentre quella vista da un aereo a diecimila metri di quota è π356². Un fattore pari a poco più di 100. Quella della stazione spaziale è π2170² con un fattore pari a solo 36 rispetto alla vista dall'aereo.

I calcoletti che sono stati fatti possono essere riprodotti attraverso la figura che segue e che si riferisce alla Stazione Spaziale...

 

ATTENZIONE! I calcoli effettuati in questo articolo sono estremamente semplificati e riguardano la proiezione bidimensionale della superficie della Terra vista dagli astronauti. In realtà quello che vedono è la superficie di una calotta sferica: QUI i calcoli più accurati svolti dal nostro amico lettore Marco Motta.

 

La Stazione

(Maurizio Bernardi - 20/7/2018)

La Stazione Spaziale Internazionale vola, dall'anno 2000, a 400 km sopra le nostre teste, alla ragguardevole velocità di 27.000 Km/ora.

Su alcuni siti , come questo  vi danno, per le principali città, gli orari del passaggio in cielo, la magnitudine e la mappa della traiettoria, così potete ammirare per una decina di minuti questo puntino luminoso che solca il firmamento sopra la vostra casa, sapendo di cosa si tratta. C'è anche questo sito della NASA in cui basta inserire il nome della località nella quale vi trovate, per conoscere gli orari dei prossimi passaggi.

Su un altro sito,  questo, potete vedere cosa vedono “loro”, dalla Stazione, ed è uno spettacolo incredibile. Se vi piace l'alba ma non vi piace alzarvi all'alba, potete vederne sedici in una sola giornata, da 400 Km di altezza, sull'oceano o sulle coste illuminate dei continenti o su paesaggi di ogni genere.

Ne parlo con gli amici, al bar della spiaggia, e subito nasce la proposta “Perché non ce la fai vedere questa notte, quando passa?”

 

Facile, basta aprire la pagina con la mappa che mostra la curva tra le costellazioni, osservare bene l'azimut da cui sorgerà e aspettare il minuto preciso. Sì, perché,  se a volte accade che i treni arrivino nelle stazioni in ritardo, le stazioni come questa  ISS  arrivano all'orizzonte sempre puntuali.

Eccola infatti, muoversi con determinazione lungo invisibili binari tra le stelle, apparentemente più veloce nel tratto vicino all'orizzonte, poi più placida in corrispondenza  alla culminazione, e di nuovo veloce, nella discesa finale, prima di scomparire all'orizzonte. Il tutto in dieci minuti.

“Non è vero che va a 27.000 km all'ora !“ Due occhietti a spillo e una vocina petulante, il figlio undicenne degli amici, rompe l'incantesimo della osservazione.

“Ma dai, se fa sedici giri al giorno, significa che per ogni giro impiega un'ora e mezza. Dato che un giro è 40.000 Km, si fa presto a fare il conto, viene proprio 27.000 km all'ora, più o meno.”

“Assolutamente No!  Se ci ha messo 10 minuti per attraversare tutto il cielo da Nord Ovest a Sud Est, vuol dire che per fare il percorso che non vediamo, da Sud Est a Nord Ovest, impiegherà altri 10 minuti, in totale 20 minuti, per fare 40.000 Km, alla velocità incredibile di 120.000 Km all'ora.”

“Ecco, carino, hai detto bene -incredibile-  perché, se fosse come dici tu, tra 10 minuti dovremmo rivederla comparire, invece non la vedremo che tra un'ora e 20 minuti.”

“E allora come si spiega?  Come fa ad attraversare metà percorso in 10 minuti? Forse che si ferma un'ora dall'altra parte a riposarsi, prima di riprendere il giro?”

“Fermarsi, non si ferma di certo. La spiegazione è semplice e ci puoi arrivare anche da solo, magari con l'aiuto di un disegnino della Terra, che ha un raggio di 6378 km, della stazione che si trova sopra di noi a 400 km e del suo percorso che puoi pensare circolare...  Così, già che ci sei, ti fai anche un'idea di quanto distante si trova da noi, nei momenti in cui sorge e tramonta”.

Può interessare anche a voi? Pensateci!

Bella immagine, vero?

Dimenticavo… ecco il disegno della piccola peste,  non male!

 

 

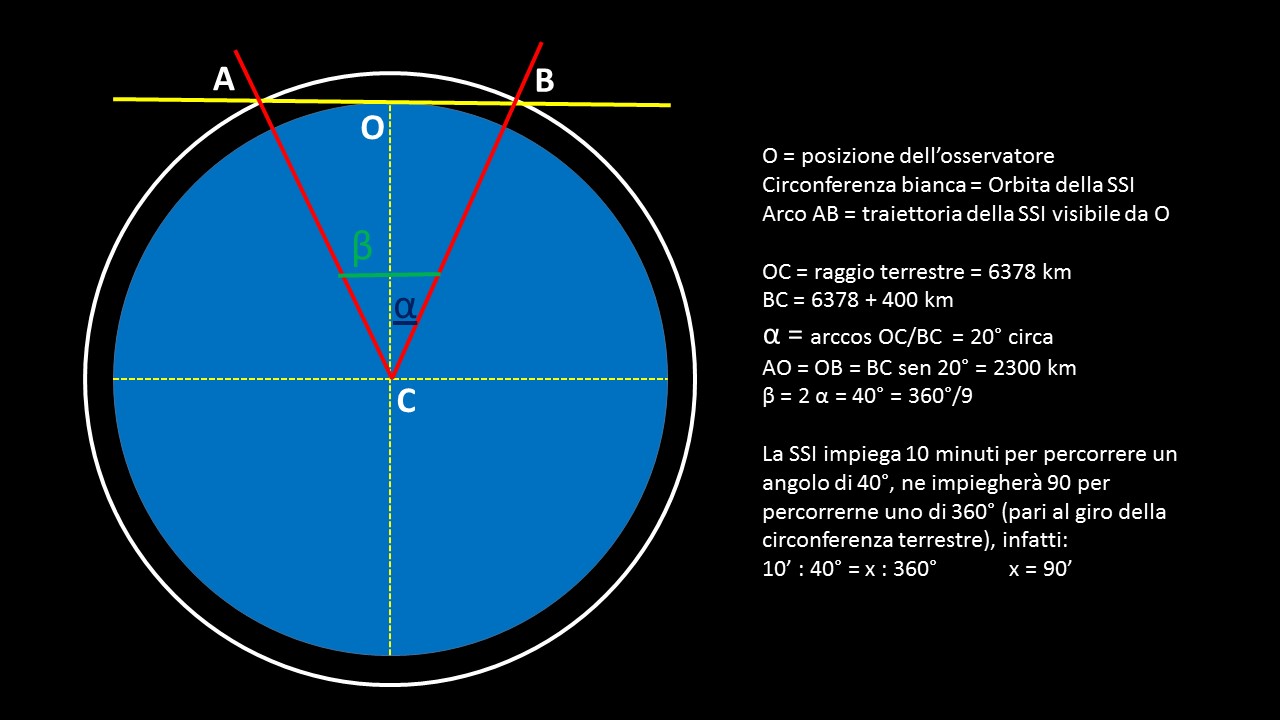
Chi non conosce la trigonometria può arrivare allo stesso risultato raggiunto dalla piccola (e precoce) peste lavorando in modo empirico con goniometro e compasso, oppure utilizzare il triangolo di Pitagora per limitarsi a trovare OB = OA, ma può anche decidere di imparare quelle poche e semplici regole spiegate QUI.

QUI la ISS vista dal balcone dell'amico Carlo Azimonti

E sarà vero che è possibile inserire in orbita un nano satellite lanciandolo con la semplice forza di un braccio dalla Stazione spaziale internazionale? Se non ci credete, guardate QUI!

QUI, invece, scoprirete come raggiugere la Iss in modo economico ed ecologico imitando una supernova.