Nei film di fantascienza si vedono, spesso e volentieri, gli astronauti che, giunti su un esopianeta qualsiasi, iniziano a muoversi tranquillamente sul suolo alieno senza alcun problema, a parte la solita tuta per permettere di respirare normalmente e altre cosucce del genere. In realtà, però, la situazione comporta un errore non indifferente, dato che trascura la gravità del nuovo pianeta.

La faccenda è piuttosto chiara: basta ricordare il primo uomo che è sceso sulla Luna. La sua passeggiata si è svolta in modo molto diverso da quelle terrestri. Se ammettiamo che la densità (massa divisa per il volume) dei corpi planetari sia sempre la stessa (ρ = M/V) basta ricordarsi la formula di Newton che ci fornisce l’accelerazione di gravità al suolo e fare qualche semplice sostituzione.

g = GM/R²

dove g è la gravità sulla Terra (più esattamente l’accelerazione di gravità…), M la massa terrestre e R il raggio terrestre. Al posto di M possiamo sostituire il prodotto tra densità e volume e si ha:

g = G4π ρ R³/3R² = (G4π/3)ρR

La parte in parentesi è una costante per qualsiasi pianeta e possiamo chiamarla K. Si ha, allora:

g = K ρR

Da cui seguirebbe che la gravità g di qualsiasi pianeta sarebbe direttamente proporzionale al suo raggio. In realtà, anche se non proprio la stessa, quella della Luna è simile alla nostra e la gravità lunare è decisamente minore di quella terrestre.

In realtà, la densità varia da pianeta a pianeta, soprattutto se pensiamo ai giganti gassosi e ai piccoli corpi del Sistema Solare.

In un recente lavoro sono stati messi in grafico i piccoli corpi del Sistema Solare e si è stabilita una certa legge che lega massa e gravità superficiale, rapportate a quella della Terra. Vediamo questa legge nella parte sinistra della figura che segue. Empiricamente si può assumere che la gravità vada con la radice quadrata della massa.

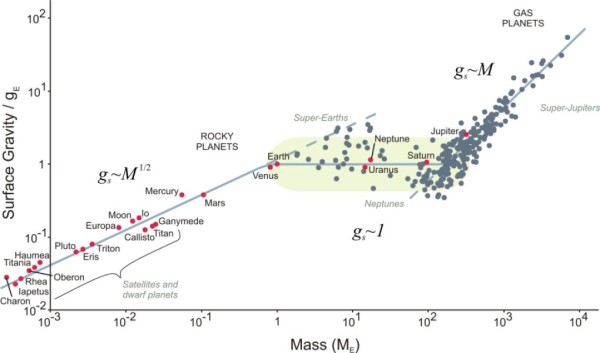
Discorso abbastanza diverso (ma non poi troppo) per i giganti gassosi di altri sistemi stellari (parte destra della figura). Anche qui c’è una chiara relazione tra gravità superficiale e massa, ma la legge va linearmente con la massa.

Fino a qui niente di veramente strano. Tuttavia, se vengono inseriti i pianeti detti "superterre" e tutti quelli che non superano la massa di Saturno si vede un andamento molto sorprendente. Essi sembrano fare di tutto per mantenere la stessa accelerazione di gravità sulla superficie.

Ovviamente, per far ciò, in molti casi (vedi Saturno o l'esopianeta recentemente scoperto che ha la stessa densità del polistirolo) la densità deve essere bassissima, ma la cosa importa relativamente poco dato che il Signore degli anelli non ha certo una superficie solida, come d’altra parte Nettuno e Urano. Resta il fatto, però, che per quelli con superficie solida, malgrado massa e raggio siano molto diversi, la gravità resta sempre abbastanza vicina a quella terrestre.

Una legge empirica che, per adesso, non ha ancora una spiegazione (sempre che sia tutto confermato in futuro). Essa, però, garantirebbe lo stesso modo di camminare per ognuno dei pianeti coinvolti: una bella comodità per gli astronauti, sia terrestri che alieni. Escludendo i “nettuniani”, avremmo, comunque, la stessa gravità (o quasi) per pianeti con una massa anche dieci volte superiore alla nostra. Niente male!

Ne segue che, in fondo in fondo, certi film di fantascienza, a prima vista un po’ “primitivi”, potrebbero avere ragione!

Leggetevi l’articolo originale, decisamente facile e ricco di altre importanti considerazioni… già il titolo stesso si rifà a Guerre Stellari!

QUI un quiz dedicato a come calcolare l'accelerazione gravitazionale di un pianeta conoscendo la distanza tra di esso e un suo satellite