Questo articolo è stato inserito in quattro sezioni dell'archivio: Astronomia classica, Velocità della luce, Spaziotempo / cosmologia e "Radiazioni di fondo: quante sono?"

 

Abbiamo spesso parlato di spaziotempo, passando dalla relatività ristretta a quella generale, dall'aberrazione ai buchi neri. Abbiamo sempre cercato di restare su un livello abbastanza comprensibile, anche se un po' di matematica è stata costretta a entrare in gioco. Grazie all'aiuto dell'instancabile PapalScherzone, che spesso sa anche essere serio e riflessivo, abbiamo voluto mettere insieme tre articoli di livello nettamente più basso che permettano una visione abbastanza completa, anche se giocoforza approssimativa, di cosa si riesce a osservare nell'Universo, quando si riesce a farlo e del come le informazioni giungono a noi. Parleremo di coni di luce, di rumore di fondo, di distanze cosmiche, di limiti e di tante altre cose che spesso spaventano, ma che possono essere semplificate per un pubblico più vasto e - a volte - timoroso. L'Universo e le sue leggi non devono spaventare nessuno, dato che anche noi siamo Universo.

 

Cosa vediamo nell'Universo

Negli approfondimenti, trovate già qualcosa di piuttosto semplice nel descrivere cosa s'intende per spaziotempo. Forse qualcosa di cui parleremo qua è anche detto là, ma, lo sappiamo tutti, ripetere certi concetti non fa mai male a nessuno.

 

Siamo fortunati o sfortunati nel vedere il Cosmo?

1. Per i più grandi **

Poniamoci una domanda: “Siamo particolarmente fortunati ad essere stati raggiunti dalla RCF (Radiazione Cosmica di Fondo) in un momento della nostra evoluzione in cui abbiamo le capacità tecniche di rilevarla? Rispondiamo ai più “grandi” tenendo conto dell’espansione dell’Universo e parlando in modo abbastanza serioso (anche se semplice).

In realtà, la domanda appare più che giustificata quando si pensa che la radiazione cosmica di fondo ha agito 380000 anni dopo il Big Bang e non è certo durata per miliardi di anni, ma solo per un intervallo abbastanza modesto di tempo. Si potrebbe allora dire: “Se è avvenuta in un certo momento della storia dell’Universo, e ciò che vediamo oggi è la luce che ha emesso in quel momento, allora vuol proprio dire che ci siamo trovati nel posto giusto, al momento giusto e con la tecnologia giusta. Qualche milioni di anni fa la luce non sarebbe ancora arrivata e tra qualche milioni di anni la luce ci avrebbe già superato”.

Il discorso sembrerebbe non fare una grinza e - oltretutto- è avvalorato da molti casi ben conosciuti.

Prendiamo, ad esempio, l’esplosione della stella che ha dato luogo alla  nebulosa del Granchio. Fu osservata a occhio nudo dai cinesi nel 1054 d.C., proprio nel momento in cui esplose come supernova. Accidenti, potremmo dire, se fosse avvenuta qualche secolo dopo l’avremmo potuta osservare con lo Space Telescope e chissà quante cose avremmo imparato. Invece, purtroppo, OGGI ci dobbiamo accontentare della nebulosa che ha creato e della stella di neutroni al suo centro. Abbiamo perso l’attimo fuggente. Che sfortuna!

Siamo stati, invece, fortunati con altre supernove e, soprattutto, con la RCF?

Non facciamo confusione: la fortuna o sfortuna nel vedere un’esplosione di brevissima durata non ha niente a che vedere con la RCF e  -se fosse possibile osservarlo- con la visione stessa del Big Bang. Perché questa differenza? Presto detto: “La supernova è avvenuta in un punto e in un momento ben preciso della storia dell’Universo, l’emissione della RCF in un momento abbastanza preciso, ma in TUTTO l’Universo di 380000 anni d’età (così come il Big Bang era TUTTO l’Universo in quel momento)

Potrebbe bastare questa frase per far comprendere l’enorme differenza. Tuttavia, diamone una spiegazione molto semplificata, ma abbastanza esauriente.

Cominciamo con una supernova qualsiasi o, se volete, con un qualsiasi fenomeno di breve durata perfettamente localizzato nello Spazio. Usiamo la solita rappresentazione di cerchi concentrici che simulano l’espansione dell’Universo nel piano del foglio. Attenzione però: in questo modo semplificato, il tempo scorre in modo radiale a partire dal centro (il Big Bang), mentre lo Spazio è rappresentato in una sola dimensione lungo la circonferenza di centro Big Bang e di raggio uguale al tempo trascorso dal momento iniziale.

Consideriamo la Fig. 1 e sull’asse delle ascisse (tempo) mettiamo la nostra Terra.

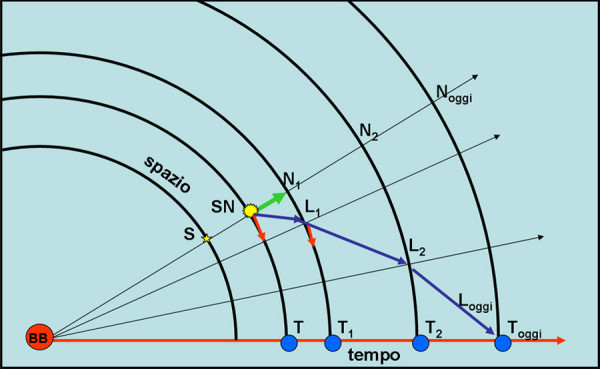
BB è il Big Bang (tempo = 0). La stella S nasce e l’Universo in quel momento è il cerchio che passa per essa. Noi (T), che scorriamo lungo l’asse del tempo, non esistiamo ancora. La stella S è costretta a muoversi in senso radiale dato che l’Universo si espande. Ad un certo momento la stella esplode come supernova (SN). Noi esistiamo già (intesi come Terra) e siamo abbastanza vicini a lei. A quale distanza? Le distanze si misurano nello spazio e lungo il cerchio che contiene la stella e T. Quindi sarà proprio l’arco di cerchio SN-T (ma ne parleremo più avanti).

Al momento dell’esplosione di S (SN) la luce si dirige alla sua velocità FINITA verso di noi (freccia rossa). Tuttavia, mentre lei cerca di raggiungerci, l’Universo si espande e i fotoni sono obbligati a seguire anch’essi questa espansione. L’espansione costringe un oggetto fermo (come SN) ad andare lungo la retta radiale BB-SN. La luce deve invece seguire sia questa direzione (freccia verde) che quella che la porterebbe verso T.

Notate che se non ci fosse espansione la luce arriverebbe a T in breve tempo, dovendo percorrere solo la distanza SN-T. Ma così non è. Quando la stella si sarà trasformata in stella di neutroni N₁ e la Terra sarà arrivata in T₁ , la luce (ossia i fotoni emessi da SN) sarà giunta solo in L₁ (questa posizione è stata costruita sommando “vettorialmente” le frecce rossa e verde - come sommare i vettori è spiegato all'inizio dell'approfondimento sul momento angolare). Se tutto si fermasse, la luce prenderebbe volentieri la direzione verso T1. La distanza è aumentata, ma non di molto. Niente da fare, però, perché l’espansione continua e quando la Terra sarà in T₂ la luce sarà giunta in L₂.

Attenzione! stiamo facendo qualcosa che sembrerebbe assurdo, ma che non lo è. Sommiamo la velocità della luce a qualche altra cosa che sembra una velocità... ma, ma, così Einstein si metterebbe a urlare! E, invece no. Niente può superare la velocità della luce nello Spazio, ma non lo Spazio stesso! La sua relatività non pone limiti alla velocità di espansione dello Spazio, e questa può tranquillamente superare anche quella della luce.

Finalmente, OGGI, la luce arriva alla Terra e noi riusciamo a vedere l’esplosione della supernova. Sono passati molti anni da quando la luce è partita, molti di più che se la luce di SN ci avesse raggiunti in T (Universo NON sarebbe stato in espansione, ma statico). Ecco perché diciamo che la SN ha una certa distanza in anni luce -ancora meglio- che la luce ha impiegato un certo numero di anni per raggiungerci. E’ l’unico modo per tenere conto sia della distanza iniziale che del tempo impiegato per raggiungerci.

Comunque sia, in questo caso siamo stati FORTUNATI. Ci siamo trovati al punto giusto, nel momento giusto e con la tecnologia giusta. Pochi anni prima avremmo ancora visto la luce della stella prima dell’esplosione e tra qualche anno solo la stella di neutroni. Nel caso della Supernova del Granchio siamo invece stati SFORTUNATI, perché la luce è arrivata IERI e oggi vediamo ormai solo la stella di neutroni che è rimasta a seguito della catastrofe cosmica. Notiamo, ancora una volta, che la VERA distanza OGGI della stella di neutroni N è l’arco di cerchio N_oggi – T_oggi.

La Fig. 1 merita qualche altra considerazione. I segmenti colorati in blu, che descrivono rozzamente il percorso compiuto dalla luce al variare del tempo (tenendo conto dell’espansione dell’Universo), dovrebbero essere costruiti per piccoli intervalli di tempo. Ci accorgeremmo allora che la luce descrive una curva un po’ strana che già conosciamo. Essa altra non è che il bordo superiore del CONO DI LUCE odierno del nostro passato, ossia l’insieme di tutto ciò la cui luce ci ha raggiunto OGGI. In altre parole, di tutto ciò che vediamo oggi dell’Universo. Un cono con una forma un po’ strana… ben diverso da quello che siamo abituati a vedere nel diagramma di Minkowski. Beh, l’unica differenza è che stiamo facendo espandere l’universo, mentre la Relatività Ristretta non teneva conto di questo fenomeno.

A questo punto, siamo in grado di passare alla Fig. 2, dove useremo soltanto le curve relative ai coni di luce in tempi diversi, tenendo però conto che la loro costruzione ha seguito la regola di Fig. 1 per descrivere il percorso della luce.

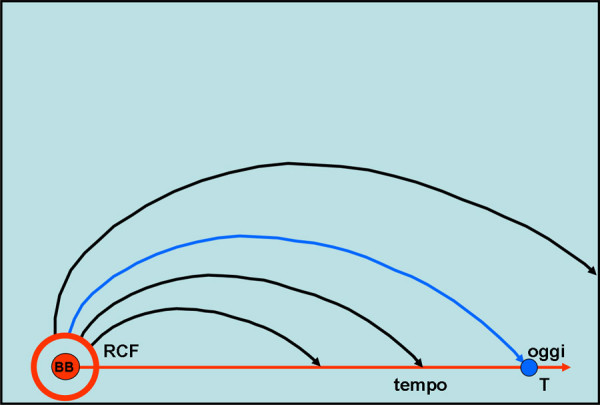
La Fig. 2 mostra diversi coni di luce del nostro passato, in diverse età dell’Universo e quindi in diversi tempi della nostra esistenza. Essi arrivano fino al momento della emissione della RCF. Attenzione però. Il fenomeno è avvenuto in TUTTO l’Universo di allora (cerchio rosso) e non solo in un punto ben definito, come per la stella S di Fig. 1. Il che vuol dire che in qualsiasi momento del nostro passato (e anche del futuro) vi saranno stati o vi saranno sempre dei fotoni appartenenti alla RCF che ci hanno raggiunto o che ci raggiungeranno.

Non fatevi ingannare dal fatto che sembra che solo un punto della RCF ci raggiunga. Nelle figure abbiamo dovuto considerare lo spazio a una dimensione, ma esso è in realtà a tre dimensioni e ciò comporta che ogni curva di luce ci fornisce una visione dell’Universo visibile al momento dell’emissione.

Ciò che cambia nel tempo è solo lo spostamento verso il rosso della luce . Ciò potrebbe comportare che nel futuro diventi invisibile con la tecnologia odierna, ma non per questo la radiazione di fondo smetterà di raggiungerci. Insomma, in questo caso NON SIAMO STATI FORTUNATI, dato che la RCF ci ha raggiunto nel passato, ci raggiunge oggi e ci raggiungerà anche nel futuro.

Per riassumere quanto detto finora e ripetere nel contempo alcuni concetti già trattati, ma mai inutili (penso), abbiamo costruito anche la Fig. 3.

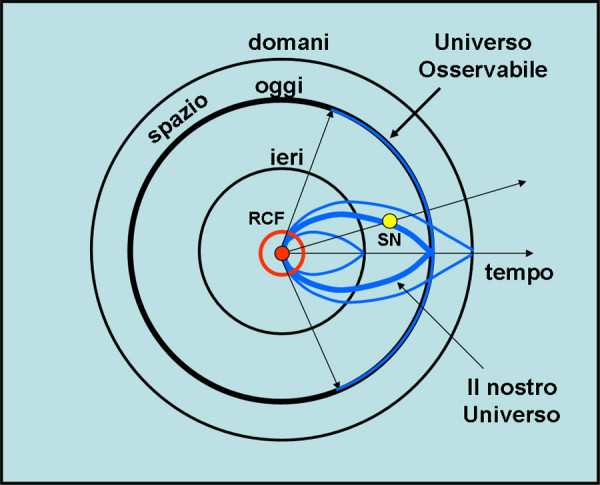
In essa si vede l’intero Universo com’era ieri (una data qualsiasi nel passato), com’è oggi e come sarà domani (un tempo qualsiasi del futuro). Per i tre Universi ho disegnato i coni di luce relativi al nostro passato (curve blu). Come potete facilmente vedere ne esiste uno e uno solo che passa per la supernova SN. Se questo è quello relativa a OGGI, vuol dire che vediamo OGGI la supernova e siamo FORTUNATI.

Invece, si vede benissimo che qualsiasi sia la nostra posizione nel tempo, il cono di luce passa SEMPRE attraverso il cerchio che rappresenta l’Universo al momento della RCF. Di conseguenza essa si vedrà sempre, ossia NON SIAMO FORTUNATI. Stesso discorso varrebbe anche per il Big Bang se solo la sua luce, ossia i suoi fotoni, riuscissero ad attraversare le prime fasi evolutive, quando la densità della materia bloccava inesorabilmente le particelle trasportatrici della luce.

La figura ci mostra anche la differenza tra l’Universo che vediamo oggi (cono di luce blu più spesso) e quello che è invece è l’Universo Osservabile, ossia l’insieme degli oggetti, nella distribuzione spaziale odierna, di tutto ciò che siamo in grado di vedere oggi (cono di luce). Esso deve stare sul cerchio che ci contiene OGGI ed è rappresentato dall’arco di cerchio blu. Come vedete, l’Universo a nostra disposizione è ben poca cosa rispetto all’intero Universo. Oltretutto è un miscuglio di spazio e di tempo e non una sua immagine istantanea.

Questa apparente limitazione è invece una grande FORTUNA (valida sempre), in quanto ci permette di vedere le varie fasi evolutive di un gran numero di oggetti celesti (non tutti, ma sufficienti a capire molto). Anche una "giusta" velocità della luce è fondamentale ai fini della nostra consapevolezza e possibilità di conoscenza dell'Universo: QUI abbiamo parlato di come essa cambierebbe se la luce fosse più veloce o più lenta.

Noterete anche che l’Universo Osservabile cresce di anno in anno, seguendo il ritmo dell’espansione. Molti altri oggetti si renderanno visibili nel futuro, ma una parte di Universo non potrà mai essere osservato. Tutto ciò, indipendentemente dallo spostamento verso il rosso che potrebbe nasconderci per sempre cose già viste, a causa dei limiti tecnologici degli strumenti che potrebbero non essere più in grado di rilevare fotoni che continueranno ad arrivare, ma il cui segnale sarà sempre più debole.

Scusate, se ho ripetuto molte cose già dette, ma penso che non sia mai troppo, quando si parla di questi concetti essenziali. Semplificazioni ne ho fatte, ma non vi sono errori “gravi”.

 

2. Per i più piccoli *

Poniamoci la stessa domanda: “Siamo particolarmente fortunati ad essere stati raggiunti dalla RCF (radiazione cosmica di fondo) in un momento della nostra evoluzione in cui abbiamo le capacità tecniche di rilevarla? Rispondiamo ai più “piccoli” senza tener conto dell’espansione dell’Universo e pensando a un vero e proprio temporale di luce. Un minimo di preparazione e poi, proprio utilizzando il diagramma di Minkowski, parliamo di cosa vediamo, quando lo vediamo e perché. Se la nuvola è molto grande, la pioggia è caduta ieri, cade oggi e cadrà domani. Un modo estremamente semplice per spiegare molte cose ai più piccoli (ma non solo)…

Ripetiamo quanto detto, utilizzando il diagramma di Minkowski. In questo modo riusciamo ad arrivare più facilmente anche ai più piccoli (?!). Una rappresentazione che è rivolta anche agli insegnanti in modo che possano usarla come traccia per le loro spiegazioni. Ci accorgeremo che non solo si dà un’idea dell’evoluzione dei corpi celesti, di quali riusciamo a vedere e quando, ma anche la differenza tra la FORTUNA di vedere una supernova e la NORMALITA’ di continuare a vedere la Radiazione Cosmica di Fondo.

Ovviamente, non teniamo conto dell’espansione dell’Universo. “Gravissimo” errore che ci costringe a disegnare un Big Bang “lunghissimo” nello spazio, al pari della RCF? No, è solo un errore “apparente”. In fondo, al tempo del Big Bang e della RCF, lo spazio era decisamente più piccolo, ma era comunque TUTTO quello a disposizione. E’ come se usassimo una scala variabile nel disegno che mantenga lo spazio sempre uguale…

Non andiamo troppo nel particolare, dato che cadremmo nelle coordinate comoventi e cose del genere. A noi basta immaginare che l’Universo sia statico e che le linee di Universo delle stelle e delle galassie siano tutte parallele tra loro. Per spiegare cosa si è fatto, può servire la Fig. 4 che mostra come “stirare” il cerchio del famoso palloncino spazio-tempo in una serie di linee parallele e perpendicolari tra loro. Tutto si semplifica enormemente. Le stelle e le galassie (immaginate ferme di per sé) si muovono solo lungo l’asse del tempo.

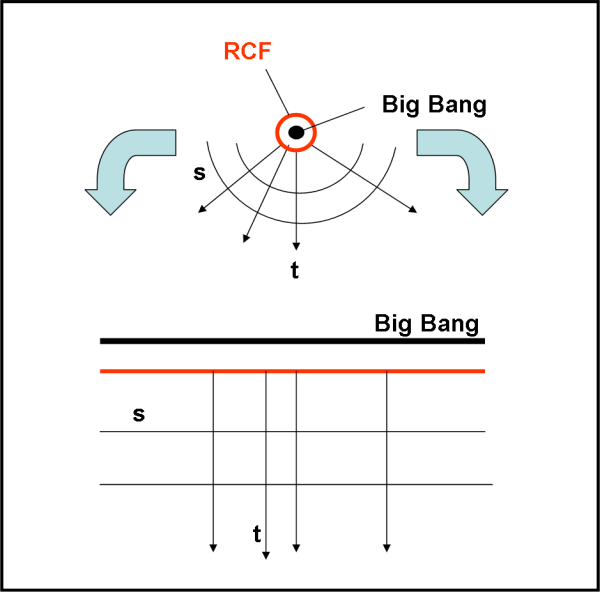
Avete visto che abbiamo ribaltato la solita figura che ha il tempo verso l’alto. L’abbiamo messo verso il basso per fare il paragone con la pioggia che cade. Ovviamente, la faccenda rimane la stessa: basta pensare che il futuro è nella parte bassa del disegno.

La retta orizzontale nera più alta è il Big Bang. Quella di poco più bassa (rossa) è la Radiazione Cosmica di Fondo, che coinvolge tutto lo spazio e, quindi, è anch’essa una retta. A partire da lei nascono le galassie e le stelle che continuano a viaggiare nel tempo lungo rette perpendicolari alla RCF, ossia lungo rette parallele all’asse del tempo.

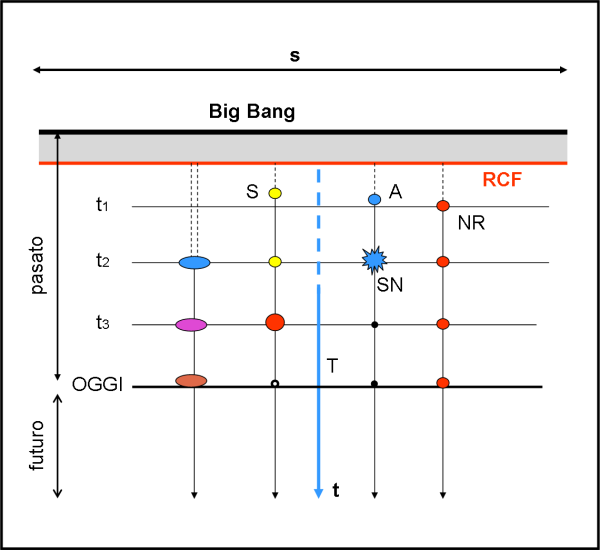
Osserviamo ora la fig. 5, una figura sicuramente banale, che però ci mostra come dal Big Bang e poi dal RCF siano “usciti” i corpi celesti come le galassie, le stelle e anche le particelle qualsiasi. Dopo la parte grigia tra Big Bang e RCF, in cui non si può vedere niente (ma non nasce nemmeno niente di veramente grande, solo le particelle e gli atomi), cominciano a cadere gocce di pioggia più o meno grandi, che si uniscono e formano i corpi celesti. Alcune si formano subito e altre più tardi. La linea azzurra è quella della Terra che si è formata a un certo punto, circa 4.5 miliardi di anni fa. La parte tratteggiata delle linee è quella relativa a quando non erano ancora nate, ma erano un gruppo di atomi in cerca di una casa comune.

E’ come se il RCF fosse il bordo di una nuvola spessa che copre tutto il cielo e le linee di Universo degli oggetti celesti i percorsi delle gocce di pioggia. Gli insegnanti possono ampliare a piacere il discorso e spiegare molto bene la nascita e l’evoluzione degli oggetti celesti di tipo diverso a partire dalla nuvola del RCF. Ad esempio, come in Fig. 5, possono rappresentare una galassia Ga che rimane più o meno la stessa. ma cambia di colore a causa dell’invecchiamento delle stelle che si raffreddano. Ma anche una stella S come il Sole che a un certo punto diventa gigante rossa e poi nana bianca. O ancora una nana rossa come NR che rimane sempre uguale. E, infine, una gigante A che dopo poco esplode come supernova SN e poi diventa un buco nero. Basta una nuvola e la pioggia che cade e l’Universo diventa alla portata immediata dei bambini…

Fin qui tutto bene. Ma a noi interessa ricevere la luce di queste “gocce”. Se ogni goccia cade verticalmente, la nostra Terra non si … bagnerà mai! Nel nostro cielo tempestoso vi è, però, un certo tipo di vento che soffia sempre lateralmente. Esso fa schizzare una parte delle gocce verso destra e verso sinistra, ma sempre e soltanto con una direzione a 45° rispetto all’asse del tempo (il perché di questa rappresentazione grafica del percorso della luce è spiegato sotto la fig. 9).

Detto in altre parole: questi “schizzi” sono la luce che viaggia con una velocità limitata, formando un angolo di 45° rispetto all’asse del tempo lungo cui si muovono gli oggetti celesti. E’ come se un vento impetuoso piegasse la pioggia-luce di 45°, permettendo all’acqua-informazione di ogni goccia di raggiungerci e mostraci la sua presenza.

Dedichiamoci alla Fig. 6, in cui vengono rappresentati questi schizzi di luce per i nostri vari oggetti.

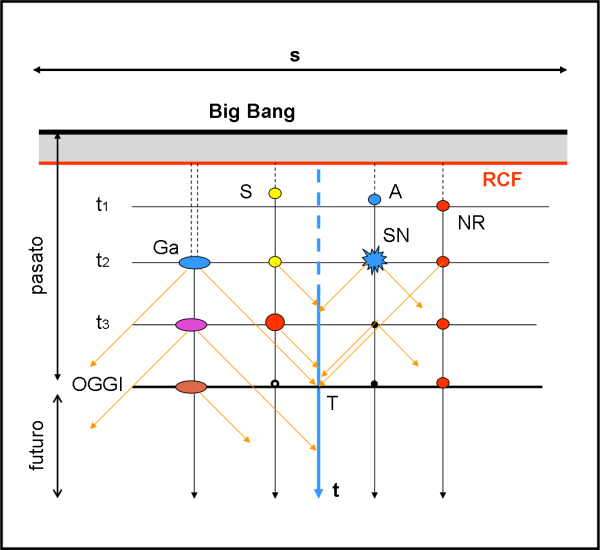
Consideriamo, una per una, le varie gocce, che possiamo anche chiamare di “materia”, se ci rivolgiamo ai più grandicelli. Analogamente,  gli schizzi possono essere chiamati “luce” che si forma quando gli elettroni delle gocce si “eccitano” un po’ troppo e creano i fotoni.

La nana rossa NR manda la sua luce al tempo t₂ ed essa ci raggiunge al tempo OGGI. Essa tuttavia rimane quasi sempre identica a se stessa e anche OGGI non è cambiata di molto (questo lo sappiamo perché, come abbiamo spiegato precedentemente, la limitatezza della velocità della luce ci consente di osservare oggi molte nane rosse a diversi stadi evolutivi).

Più interessante risulta la stella A, la gigante, che, quando arriva in t₂, esplode come supernova. La sua luce ci raggiunge abbastanza in fretta, ma troppo presto per l’uomo che non era ancora nato. Accidenti siamo stati SFORTUNATI e non riusciremo mai a vedere il momento dello scoppio. Ci dobbiamo accontentare della luce (della materia espulsa) di un buco nero che ci raggiunge oggi.

La stella S manda la sua luce di stella normale in tempi antichi, ma quando è diventata gigante rossa, e la sua luce ci ha raggiunto, avevamo già qualche strumento e siamo riusciti a vederla. Oggi e nel futuro la vedremo, però, come nana bianca con il suo bell’anello detto nebulosa planetaria (ma solo per poco tempo). Anche qui bisogna essere fortunati.

Vediamo oggi anche la luce della galassia Ga, ma relativa a quando era molto giovane.

In questo modo è facile far notare varie cose importanti, tra cui quella di osservare contemporaneamente cose antiche accadute in tempi diversi, a seconda della distanza da noi e, come conseguenza, del percorso che ha dovuto fare la luce per raggiungerci. Fortuna e sfortuna nel vedere un fenomeno oggi risulta perfettamente chiaro.

Adesso, cancelliamo tutte le stelle e le galassie e consideriamo, in Fig. 7, solo la nube temporalesca del RCF. L’unico oggetto che esiste siamo noi (T) che ci muoviamo lungo la linea del tempo.

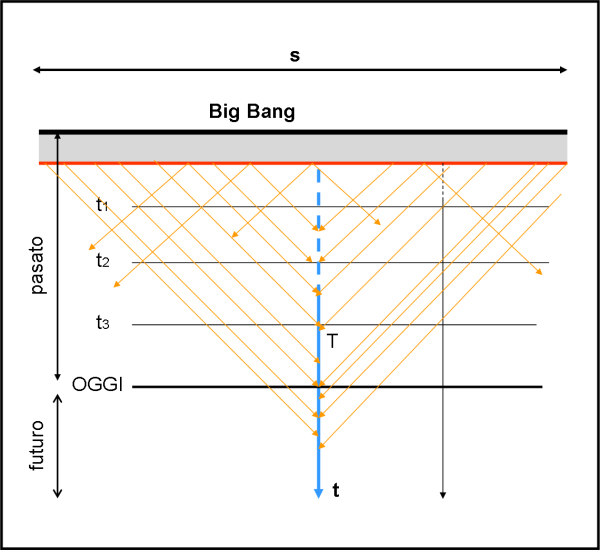
La nube RCF vuole farsi notare e ogni suo punto invia i suoi schizzi di luce (sono i fotoni che sono riusciti a trovare spazio per uscire allo scoperto…). E’ un vero e proprio temporale che ha inviato i suoi schizzi tutti nello stesso istante, quello brevissimo del RCF. Se guardiamo la figura, però, ci rendiamo subito conto che alcuni schizzi ci hanno raggiunto, che altri ci raggiungono e altri ancora ci raggiungeranno nel futuro. Ovviamente, più gli schizzi di luce sono partiti da lontano più tempo ci mettono a giungere a noi. Purtroppo (o per fortuna) pioverà sempre.

Si possono aggiungere due considerazioni un po’ più difficili:

(1) maggiore è il percorso che fa lo schizzo di luce e più arriva a noi stanco, arrossato, fino a che, in futuro, pur arrivando, non riusciremo a vederlo.

(2) Nella figura si vede che al massimo possono arrivare DUE schizzi nello stesso istante, provenienti da punti molto diversi del RCF. Questa è solo un’impressione dovuta al fatto che abbiamo disegnato lo spazio in una sola dimensione. Se, già, lo disegnassimo a due dimensioni, verrebbe fuori un cono con il centro nel punto in cui siamo noi (e non più solo due linee): avremmo descritto il CONO DI LUCE. Ma la “vera” rappresentazione sarebbe uno spazio a tre dimensioni, di cui non riusciremmo a fare nessuna figura dato che saremmo in uno spazio a tre dimensioni con una dimensione supplementare data dal tempo (verticale). Disegnare a quattro dimensioni non è ancora possibile o, almeno, molto, molto più complicato.

Fatemi finire con un disegno (Fig. 8 ) che andrebbe bene per le scuole elementari. Al posto della RCF mettiamo proprio una nuvola. Al posto degli oggetti celesti delle grosse gocce di “materia” e al posto della luce dei veri schizzi. Dal RCF continua però a cadere una pioggia sottile sottile.

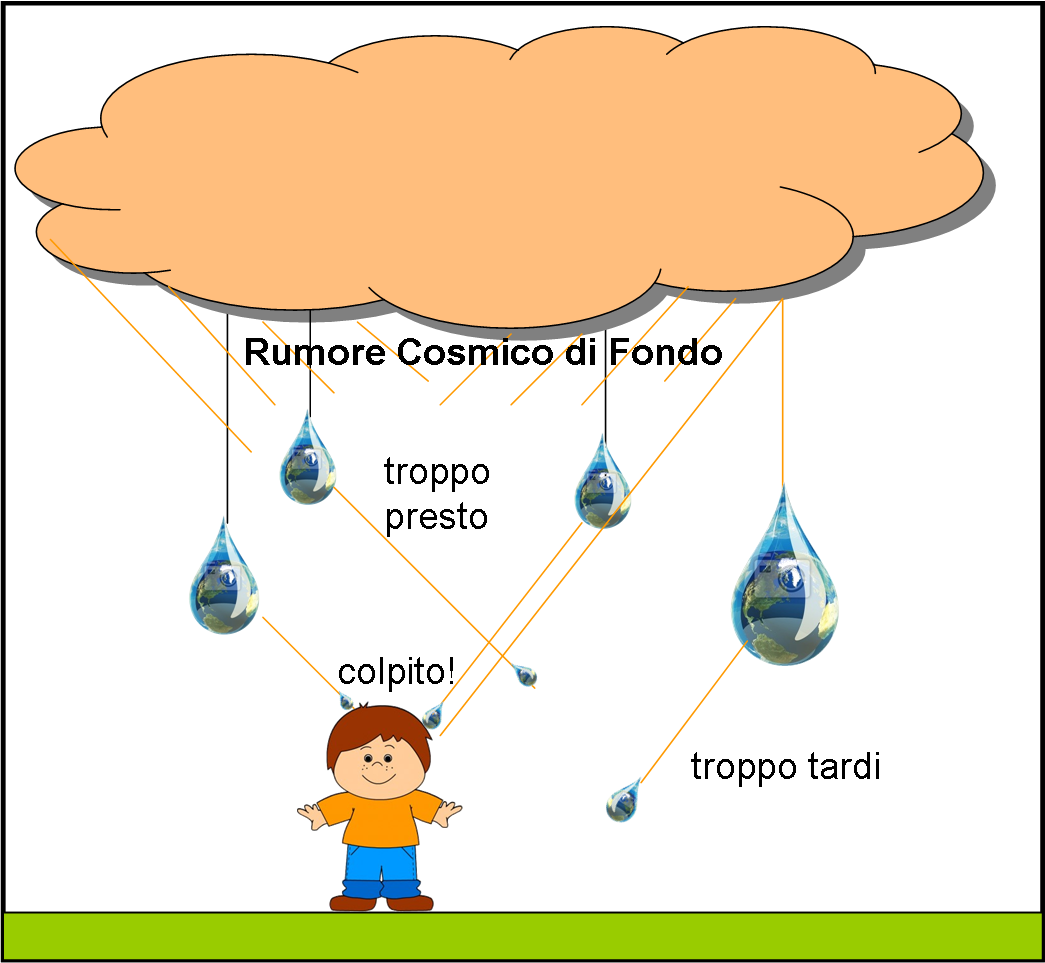
Una figura ideale per spiegare tante belle cose ai bambini e avvicinarli allo spaziotempo e ai segreti meravigliosi dell’Universo. Ma non ditegli che avete usato nientemeno che il diagramma di Minkowski!

 

Universo Osservabile  (senza espansione) *

Ne abbiamo già accennato precedentemente, ma penso valga la pena, per molti dei meno esperti, riassumere le idee in modo estremamente divulgativo. Perfino i nostri amici Astericcio & co. hanno fatto la sua conoscenza, attraverso un colloquio che sembrerebbe del tutto estraneo all’argomento.

Innanzitutto, un paio di premesse. Qualsiasi grafico o schema che rappresenti l’evoluzione dell’Universo contiene degli errori. D’altra parte è impossibile descrivere su un foglio un qualcosa che rappresenti le quattro dimensioni, di cui una, il tempo, è anche estremamente particolare.

Pur accettando una semplificazione che rasenta il limite della realtà dei fatti, è estremamente importante capire sempre che il suo valore è soltanto indicativo, a grandi linee. Guai a considerare realistica qualsiasi rappresentazione vi venga data. Una per tutte, il palloncino che si gonfia.

Essa rappresenta un modo estremamente sintetico e immediato per comprendere l’espansione dell’Universo e la crescita continua delle distanze tra i corpi che lo abitano. Ma, non cerchiamo assolutamente un collegamento diretto e semplice con la curvatura dello spaziotempo, di cui si sente parlare spesso e volentieri. Sono due cose estremamente diverse! L’espansione vede, nella superficie sferica che si allarga sempre più, un’ottima rappresentazione fino a un certo livello, permettendo di comprendere alcuni concetti essenziali come appunto l’Universo Osservabile.

La curvatura dello spaziotempo è invece qualcosa che ha bisogno della relatività generale di Einstein, in quanto racconta l’immane lotta tra espansione e gravità. Essa porta alla definizione di “forma” dell’Universo, concetto del tutto estraneo alla forma che intendiamo noi. La forma di una scatola o di una persona ci dice come la massa sia sistemata entro certi confini, mentre la forma dell’Universo ci dice “solo” che tipo di geometria può essere usato per descriverlo. In questo senso è pericolosissimo pensare al palloncino che si gonfia come a una visione della curvatura dello spaziotempo. Per il nostro livello, sono concetti del tutto estranei tra di loro, che potrebbero unificarsi solo attraverso trattazioni ben più complesse. Non diciamo altro per non confondere le idee, ma cerchiamo di ricordare sempre di non prendere le rappresentazioni divulgative come “oro colato”.

Bene, fatte queste dovute premesse, occupiamoci del concetto di Universo Osservabile, un vero e proprio limite della nostra conoscenza attuale, impostoci dall’espansione dell’Universo, ma che esisterebbe comunque anche per un Universo statico, che sia da sempre stato come è oggi. La sua limitatezza dipende sempre e soltanto dalla velocità della luce, molto alta per noi, ma non per le distanze dell’Universo.

Iniziamo con questa seconda ipotesi (attenzione che non sono molti anni che è stata scartata… lo stesso Einstein c’aveva creduto).

Immaginiamo che l’Universo sia nato, improvvisamente, 13.7 miliardi di anni fa. Nato già bello che costruito come teatro di sfondo, al cui interno si sono formati gli attori come le particelle elementari, gli atomi, le molecole, le stelle, le galassie e tutto ciò che volete, in tempi relativamente brevi. Qualcosa di simile alla descrizione della pioggia fatta precedentemente.

Il suo enorme vantaggio è che due stelle nate a una certa distanza una dall’altra mantengono sempre la stessa distanza al passare del tempo. Non parliamo di variazioni di distanza locale, dovute a mutue interazioni gravitazionali, ma alla distanza legata alla crescita dell’Universo. Facciamo molto prima a disegnare la Fig. 9.

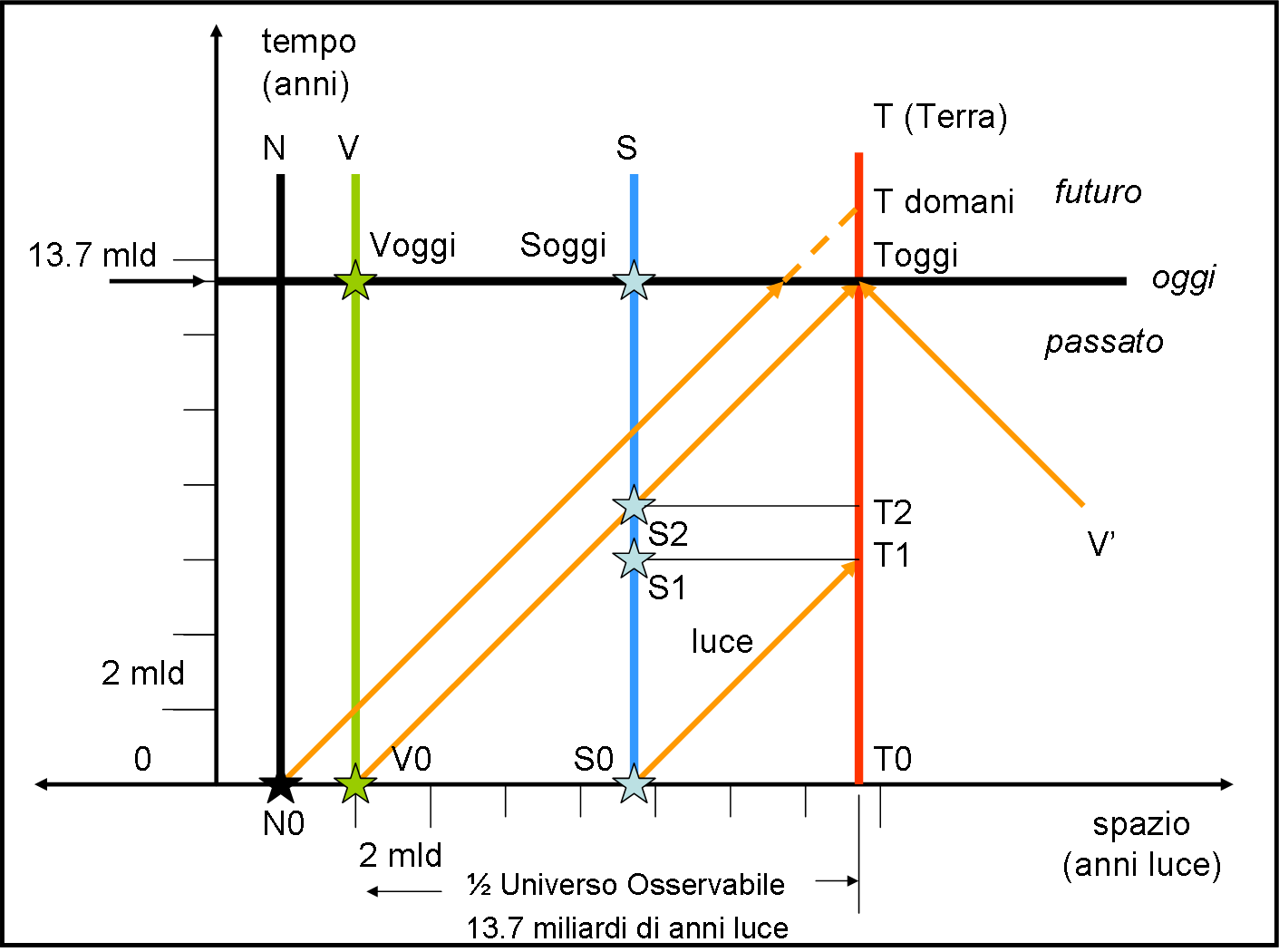
La linea della ascisse (x) è lo spazio (tre dimensioni trasportate in una sola, ricordiamocelo bene, come farlo lo abbiamo spiegato QUI alla figura 6), quella delle ordinate (y) è il tempo che scorre. Quale unità di misura prendiamo? Beh… qualcosa che aiuti a descrivere il movimento della luce, l’unico tipo di informazione che ci proviene dall’Universo (per luce si intende qualsiasi tipo di radiazione elettromagnetica, sia luce visibile, che raggi X, raggi gamma, e onde radio). O, meglio, anche se non è più l'unica informazione che ci arriva (come abbiamo raccontato QUI) è senza dubbio quella che, dato l'attuale livello della nostra tecnologia, è più facile analizzare ed interpretare.

Consideriamo, quindi, la luce l’unica informazione che una stella può mandare a un’altra stella (o pianeta o quello che volete), con i suoi pregi e i suoi limiti.

All’istante t = 0 nasce l’Universo e possiamo anche dire che nascono le varie stelle S,V,N, ecc., anche se ci vuole un po’ di tempo prima che un ammasso di idrogeno diventi una vera stella. Tuttavia, l’approssimazione ha poca importanza per il nostro discorso. Al posto della stella Sole, mettiamo direttamente la Terra T (per la scala del Cosmo, coincidono perfettamente). Abbiamo messo la Terra più o meno al centro del grafico solo per motivi egoistici, ma ricordiamoci che l’Universo non ha un centro! Qualsiasi stella può benissimo e giustamente considerarsi al centro. E ricordiamoci che l'aveva intuito perfettamente già il grandissimo Giordano Bruno.

Ciò che conta sono le distanze relative e non le distanze rispetto a una qualsiasi origine che non esiste. In una figura del genere non esiste Big Bang, ma lo spazio-tempo nasce tutt’assieme (o è sempre esistito in un’altra forma senza emissione di luce), e poi rimane quello che è, senza espandersi. Il Big Bang può essere considerato, perciò, la retta delle ascisse, al tempo t = 0.

Torniamo alle unità di misura. Lo spazio unitario può essere considerato quello percorso dalla luce in un certo intervallo di tempo (spazio misurato in anni luce). Quello delle ordinate proprio questo intervallo di tempo (tempo misurato in anni).

Ammettiamo, per esempio, di mettere una tacchetta nell’asse delle x a ogni intervallo di spazio corrispondente a quello percorso dalla luce in due miliardi di anni (è facilissimo trasformarlo in chilometri, ma avremmo un po’ troppe cifre da scrivere…). Le tacche dell’asse del tempo sarebbero intervallate proprio da due miliardi di anni. Come si muove la luce in questo semplice diagramma? Beh… è veramente banale. Essa percorre un intervallo unitario delle x (due miliardi di anni luce) proprio in un intervallo di tempo unitario (due miliardi di anni). In poche parole, essa descrive una retta inclinata di 45 gradi rispetto agli assi x e y, in modo che ogni suo punto abbia sempre l’ordinata y uguale all’ascissa x, ossia la retta y = x.

L’asse delle y non è, però, infinito. Esso si ferma al punto OGGI, un punto che corrisponde a 13.7 miliardi di anni, ossia all’età dell’Universo (come lo pensiamo noi)! Invece l’asse delle x può essere anche infinito, dato che non sappiamo quanto sia esteso l’Universo (le cui “dimensioni”, però, restano sempre uguali).

In questo diagramma, le stelle non si muovono nello spazio, ma solo nel tempo e, quindi, descrivono rette parallele tra di loro e all’asse del tempo (perpendicolari all’asse dello spazio). le possiamo chiamare linee di Universo.

Consideriamo una stella S che invii la sua luce nell’Universo all’istante t₀. La luce si muove secondo una retta inclinata di 45° e raggiunge la Terra in T₁. In quel momento la Terra vede la stella, ma la vede com’era al tempo in cui è partita la sua prima luce, ossia al tempo t = 0.

Nel frattempo, però, la stella si è mossa nel tempo ed è già arrivata in S₁. La distanza tra T₁ e S₁ (distanza al momento dell’arrivo della luce) rimane invariata ed è uguale a T₀S₀ (distanza al momento della partenza della luce).

Come abbiamo detto l’Universo non si espande e le stelle non si muovono: la loro distanza rimane la stessa in ogni istante. Tuttavia, a causa della lentezza della luce, noi vediamo in T₁ la luce partita da S₀ e non certo quella che sta inviando da S₁. In S₁ la stella potrebbe anche non esistere più, ma io la vedrei comunque all’istante in cui T raggiunge T₁, dato che sto ancora guardando la luce-informazione partita quando era appena nata, ossia quando era in S₀.

Portiamoci adesso al tempo T_oggi. Se esistesse ancora, vedremmo la stella S com’era nel momento in cui ha “sparato” la luce che arriva oggi. Ossia vedremmo la stella com’era in S₂, quando la Terra era ancora in T₂. La luce impiega del tempo per percorrere la distanza S₂T₂ = S₀T₀ = S₁T₁ e colpisce la Terra solo oggi.

Ripetiamo: oggi vediamo la luce della stella, inviata quando era in T₂. Tuttavia, oggi, la stella S ha continuato a muoversi nel tempo e quindi la sua posizione attuale è S_oggi. Poco male, la distanza effettiva tra la Terra T_oggi e la stella S_oggi è sempre la stessa ed è uguale a S₀T₀, com’era all’inizio dell’Universo. Come sarebbe bello se fosse veramente così…

Tuttavia, siamo interessati a scoprire la stella, osservabile oggi, più lontana possibile, quella che determina una specie di siepe oltre alla quale non si può vedere niente. Quale sarà? Semplice… quella la cui luce inviata al tempo t = 0 (ossia la sua prima luce) arriva solo oggi.

E’ facile trovarla, basta mandare indietro la luce fino a che incontri l’asse dello spazio, ossia fino all’istante t = 0. Questa stella è, quindi, V. Ripetiamo: la sua prima luce ci arriva solo oggi. Una stella più lontana, come N, non riusciamo ancora a vederla, dato che la sua luce ci raggiungerà solo domani, come indica la linea tratteggiata. Essa fa parte di ciò che esiste, ma sta oltre la siepe. E’ un attrice dell’Universo, ma un’attrice che non conosciamo ancora. La conosceremo solo domani, com’era, però, al momento in cui mandava i suoi primi vagiti.

Facciamo un piccolo calcolo. Quanto tempo è passato da quando la luce di V è partita? Presto detto: esattamente 13.7 miliardi di anni, l’età dell’Universo. La linea percorsa dalla luce viaggia a 45°, ne segue, quindi, che la distanza V₀T₀  è uguale a 13.7 miliardi di anni luce. Ricordiamo sempre che le distanze si misurano lungo le linee orizzontali, mentre il tempo lungo quelle verticali, La linea spaziotemporale della luce inclinata a 45° ci dice solo che un certo numero di anni luce (distanza) viene coperta nello stesso  numero di anni (tempo).

Dove si trova adesso la stella V? Esattamente in V_oggi (anche lei viaggia solo nel tempo come la Terra). La distanza V_oggiT_oggi è però uguale a V₀T₀.

In ogni modo, malgrado l'estrema semplicità, chiamiamo Universo Osservabile il doppio della distanza V_oggiT_oggi. Perché il doppio? Perché ci sarà una stella dall’altra parte della Terra che farà la stessa cosa e quindi lo spazio contenente tutte le stelle che siamo riusciti a vedere fino a oggi deve essere uguale da una parte e dall’altra, e, quindi, l’Universo Osservabile è proprio il doppio di V_oggiT_oggi = V₀T₀.

In altre parole, l’Universo Osservabile indica la posizione odierna di tutto ciò la cui luce ci sta raggiungendo oggi. Ovviamente, la luce può provenire sia da oggetti vicini (la loro prima luce ci ha raggiunto per la prima volta molto tempo fa) sia da oggetti lontanissimi (la loro prima luce ci raggiunge oggi per la prima volta). Esso è limitato, in quanto non contiene “ancora” i corpi celesti la cui prima luce non ci ha ancora raggiunto. E, perciò, ben diverso dall’intero Universo che potrebbe essere enormemente più grande, ma di cui non abbiamo ottenuto informazione alcuna (e potrebbe darsi che mai l’otterremo).

Vale la pena spiegare meglio questo concetto, spesso male interpretato… Lo facciamo per un Universo statico e lo rifaremo per un Universo in espansione. Ci aiuta la Fig. 10.

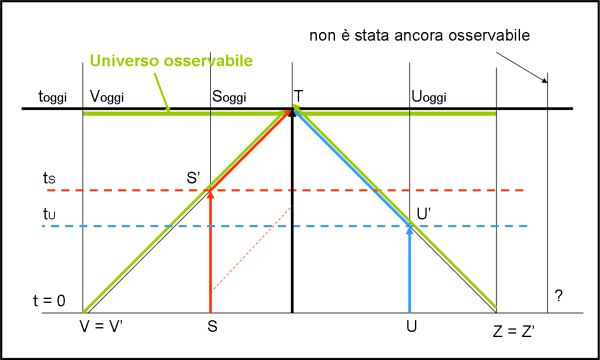
Quali sono le stelle la cui luce ci raggiunge oggi? Beh… la luce deve giungere a noi in modo da formare un angolo di 45° con la direzione del tempo. Così deve fare quando parte e così deve fare quando arriva (è come se partissimo da oggi e seguissimo, indietro nel tempo, la luce che ci sta raggiungendo).

Consideriamo la stella S che si muove, come tutte, in senso verticale. La sua luce ci ha già raggiunto nel passato (come mostra la linea diagonale rossa a trattini), ma a noi interessa quella che ci raggiunge OGGI. Per cui, tracciamo da oggi la linea a 45° fino a incontrare la linea di Universo della stella S in S’. La luce della stella S che riceviamo OGGI è quella partita da S’ al tempo t_s. In altre parole, la stella S che vediamo oggi è quella che apparteneva all’Universo tratteggiato in rosso, relativo al tempo t_s. Dove si trova la stella S, OGGI? Presto detto in S_oggi, dato che deve appartenere all’Universo di oggi. Cosa analoga capita alla stella U. Oggi riceviamo la luce che ha inviato quand’era in U’, al tempo t_U, nell’Universo relativo a quel tempo. Particolare importanza ha la stella V e  sua “sorella” Z. Anche la loro luce arriva OGGI, ma è partita proprio all’inizio del tempo, quando t = 0.

Ne deriva che la luce delle stelle più lontane di V e Z , all’origine dei tempi, NON può ancora essere arrivata fino a noi. Lo farà domani o dopodomani o tra un miliardo di anni, ma per adesso NON E’ ANCORA STATA OSSERVABILE.

L’Universo Osservabile OGGI ha, perciò, come confini le posizioni delle stelle Z_oggi e V_oggi e contiene tutte le stelle più vicine (osservate per la prima volta in tempi diversi), nella posizione che hanno OGGI (U_oggi e S_oggi). L’Universo Osservabile di OGGI è, infatti, la linea orizzontale che passa per T, di cui l’Universo osservabile è il suo tratto verde.

Riassumendo: noi oggi riceviamo la luce di stelle partite in tempi diversi. La loro posizione attuale costituisce l’Universo Osservabile. Come vedete, in queste definizioni si parla di arrivo della luce, non di sua rilevazione. I nostri telescopi potrebbero non essere in grado di  “vedere” qualcosa, anche se teoricamente la luce è arrivata. Non confondiamo, quindi, Universo Osservato realmente (e posizione attuale delle stelle osservate), dipendente dai nostri limiti tecnologici, con Universo Osservabile che dipende solo dalla velocità della luce.

Finora, le distanze tra le stelle si sono mantenute costanti, facilitando la comprensione. Tuttavia, la situazione è già stata sufficiente per la definizione di Universo Osservabile.

Essa è anche sufficiente per un’altra definizione, quella di Cono di Luce. Esso non è altro che il triangolo formato dalle linee della luce VT_oggi e ZT_oggi ed è identificato dalle linee di luce degli oggetti che ci raggiungono oggi. Al suo interno sono contenute tutte le linee di luce delle stelle già osservabili in tempi passati. Le stelle, le cui linee di Universo sono sempre state esterne a questo triangolo di luce, non fanno ancora parte del nostro Universo Osservabile odierno.

In poche parole, il Cono di Luce rappresenta il nostro passato con le uniche informazioni (luminose, ma non solo) ricevute dall’Universo. Noi non possiamo vedere l’Universo Osservabile come è OGGI, ma possiamo vedere le stelle che lo compongono come erano in tempi diversi (antichissimi per le più lontane e  recentissimi per le più vicine). Un esempio? La galassia di Andromeda la vediamo com’era circa due milioni e mezzo di anni fa, mentre il Sole lo vediamo com’era otto minuti fa!

Da come è stato costruito, ogni stella dell’Universo ha un suo Universo Osservabile, diverso dal nostro o parzialmente o completamente. Ce lo mostra la Fig. 11.

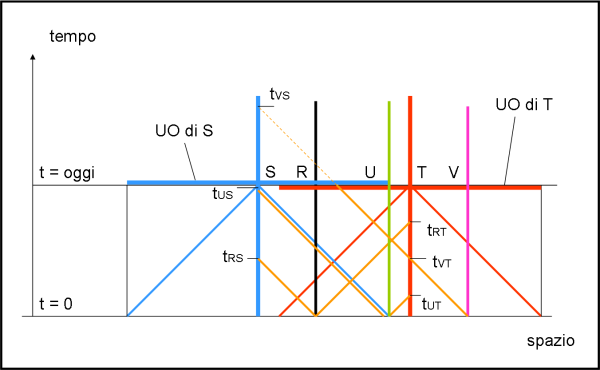
Consideriamo la Terra T e la stella S, con le loro linee di Universo rossa e blu, rispettivamente. Al tempo OGGI, esse hanno i loro Universi osservabili, descritti dalle linee orizzontali rosse e blu. Si vede bene come essi abbiano solo una parte in comune. Facciamo qualche semplice esempio.

La stella R (nera) invia la sua prima luce sia a sinistra che a destra. Essa raggiunge la Terra al tempo t_RT e la stella S al tempo t_RS , ben prima di oggi._. Essa, quindi, appartiene all’Universo Osservabile odierno sia di S che di T. D’altra parte si vede bene che oggi la stella R appartiene sia al tratto orizzontale rosso che a quello blu. Potete controllare da soli, come piccolo esercizio, che la stella U (verde) appartiene anch’essa a entrambi gli Universi osservabili (anche se è al limite di quello di S: la prima luce di U raggiunge S solo oggi). Ben diversa è la situazione della stella V (viola), che appartiene all’Universo osservabile di T, ma non a quello di S. Ne farà parte solo nel futuro, al tempo t_VS.

Dalle figure precedenti possiamo notare che tutte le stelle visibili oggi dalla Terra, sono relative a posizioni che stanno lungo le rette della luce che individuano l’Universo osservabile. Sembrerebbe vederle tutte nella stessa direzione… Non commettete questo errore! Noi abbiamo considerato lo spazio a una dimensione. Basterebbe considerare un piano (due dimensioni) e avremmo un cono descritto dalle linee della luce e non più un triangolo (da cui il nome), come mostra la Fig. 12.

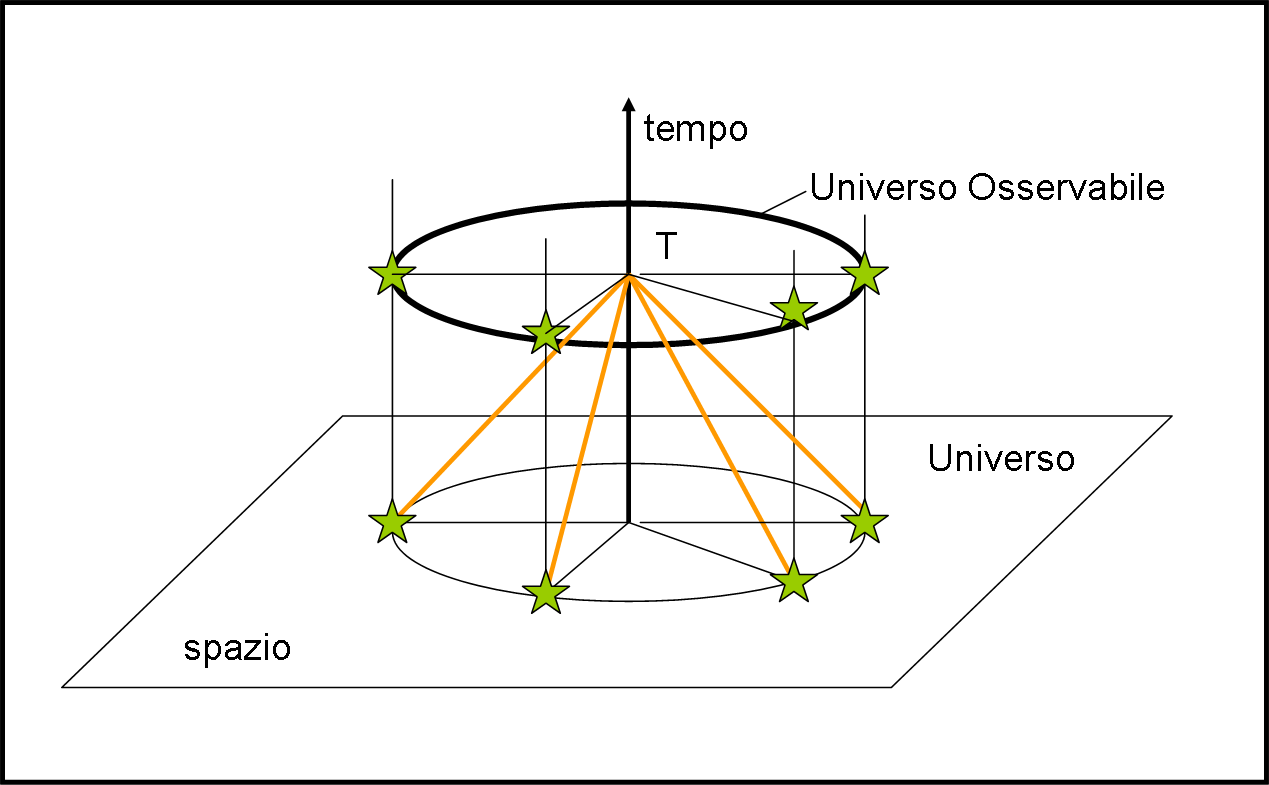
Ci manca ancora una dimensione spaziale, ma non possiamo proprio disegnarla… E questo comporta la necessità di limitarci a una o al massimo due dimensioni spaziali. Il vero Universo avrebbe bisogno di una figura ben più complicata… ma irrealizzabile.

Notiamo anche che l’Universo Osservabile di oggi è più piccolo di quello di domani e più grande di quello di ieri. E’ facile mostrare come varia l’Universo Osservabile di T al passare del tempo, come mostrato in Fig. 13 (costruitevela da soli, come esercizio).

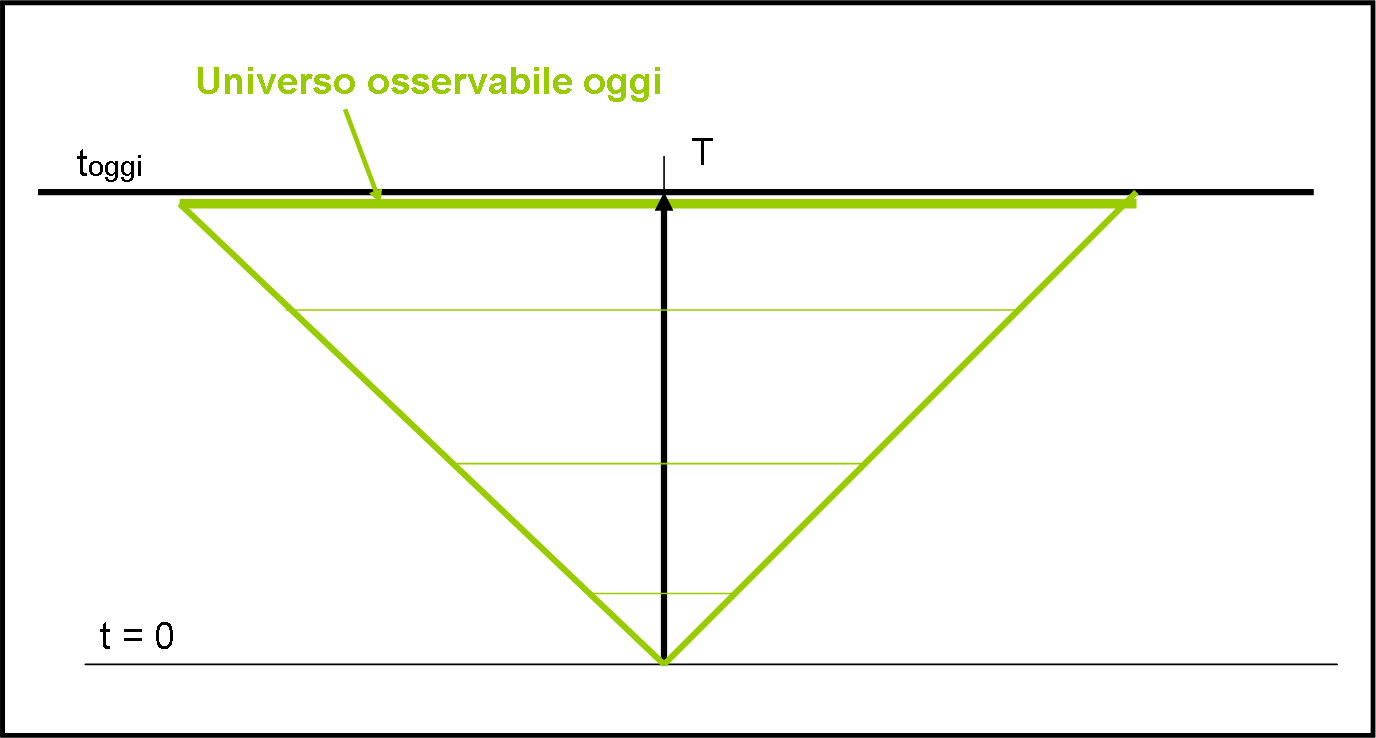
In ogni modo, potete verificare che, in questo caso semplificato in cui abbiamo ipotizzato un universo statico e non espansione, l’Universo Osservabile è sempre uguale allo spazio percorso dalla luce negli anni trascorsi dalla nascita dell’Universo.

Le cose diventano più complicate, ma non poi tanto, considerando un Universo in espansione.

Attenzione! Talvolta può accadere di vedere una figura simile alla Fig. 9 anche con l’Universo in espansione. Ciò si riesce a realizzare conoscendo di quanto si espande l’Universo (in media) e cambiando coordinate in modo che essere rimangano sempre uguali. Stiamo parlando di coordinate comoventi. Ma, questo tipo di rappresentazione comporta passaggi più complessi e meno intuitivi per cui non lo tratteremo (almeno per adesso).

 

Universo Osservabile  (con espansione) **

La prima idea, che potrebbe venire in mente, sarebbe quella di utilizzare la Fig. 9, tracciando però le linee temporali percorse dalle stelle inclinate tra loro, in modo che col passare del tempo si allontanino le une dalle altre. Esse sarebbero, comunque, le linee di Universo, ossia le linee che percorrono gli oggetti celesti (gli attori) in balia soltanto del tempo che passa e dell’espansione del teatro in cui vivono (l’Universo appunto).  Il nome del nostro Circolo nasce quasi spontaneamente…

Bene, proviamo a disegnare la Fig. 14.

Possiamo mantenere l’asse dello spazio come linea orizzontale? Potremmo anche farlo, ma al momento iniziale esiste solo un punto BB, il Big Bang e parlare di spazio sarebbe del tutto assurdo. Tutto lo spazio esistente è solo quel punto.

Dato che tutto si espande da un punto, mettiamolo pure in centro, dato che al tempo t = 0 esiste solo lui. Pensiamo, in qualche modo, che dentro di lui siano concentrate tutte le particelle che diventeranno poi atomi, stelle e galassie. Il tempo può rimanere l’asse verticale, come in Fig. 9?

Beh… è un po’ difficile, dato che ogni stella si muove in una direzione diversa e un tempo non può favorire una stella piuttosto che un’altra, anche se si tratta della nostra stella. Perché noi sì e le altre stelle no? Inoltre, abbiamo detto che ogni stella si muove solo lungo l’asse del tempo. Ne segue che ogni direzione, ossia ogni linea di Universo può essere considerata come linea del tempo.

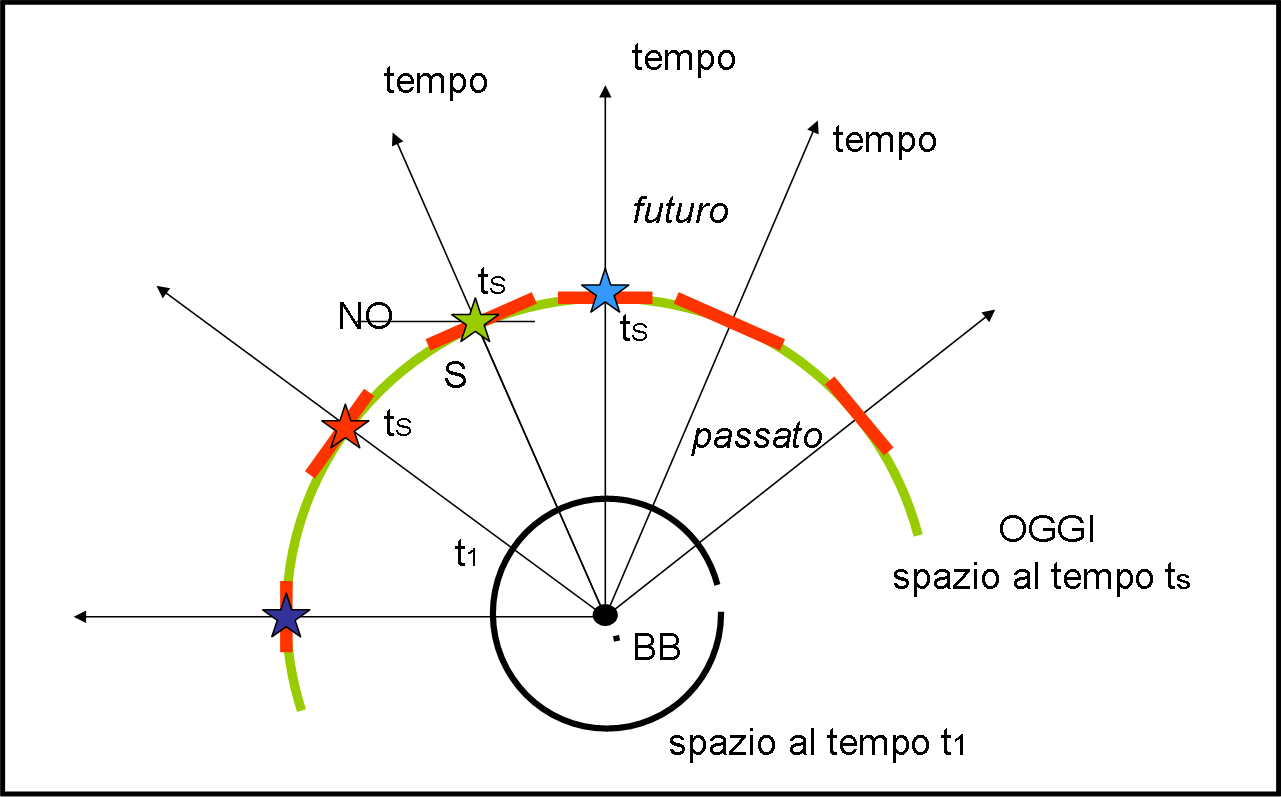
Prendiamo una stella S (verde) a un certo tempo t_S lungo la sua linea di Universo. Fatto? OK.  Adesso non ci rimane che far partire, da lei, la luce. Sappiamo che deve formare un angolo di 45° con l’asse del tempo, ossia con la linea BB – S.

Accidenti! Ma allora lo spazio non può essere la linea orizzontale, altrimenti l’angolo tra luce e linea dello spazio non sarebbe di 45°. Siamo costretti a disegnare uno spazio particolare anche per ogni stella. Proviamo a farlo, anche se la cosa sembrerebbe un po’ complicata. Comunque sia, essa deve essere la linea rossa che passa per S ed è normale alla linea del tempo. Non dobbiamo però dimenticare che a un certo tempo t_S di una certa stella, tutto l’Universo deve essere rappresentato da una sola linea (una dimensione). Il tempo t_S  è uguale per tutte le stelle (anche se con direzioni diverse) e tale deve essere anche lo spazio in quel momento, ossia l’Universo al tempo t_S.

Il modo per risolvere la questione esiste ed è anche semplice… Ogni linea rossa (spazio relativo a un singola stella) può essere considerata una tangente alla circonferenza che ha come raggio proprio il tempo passato t_S , che è uguale per tutte le stelle in un certo istante t_S. La circonferenza verde è quindi lo spazio che ci serve. Esso prende il posto dell’asse x della Fig. 9. Uno spazio curvo, ma solo per motivi di rappresentazione grafica.

Una rappresentazione simile può anche essere trasportata nelle due dimensioni dello spazio e invece della circonferenza si può utilizzare una superficie sferica.

Ed ecco perché si utilizza il palloncino che si gonfia…

In ogni punto della circonferenza o della superficie sferica si può tracciare la tangente e disegnare il percorso della luce che parte da quel punto.

La cosa veramente importante da capire è, però, che lo spazio è SOLO e SOLTANTO la circonferenza che in un dato istante passa da tutte le stelle o, nelle due dimensioni, la superficie sferica, che fa la stessa cosa.

Ciò che sta dentro alla circonferenza (o alla superficie del … palloncino) non esiste più e rappresenta il passato delle stelle, della luce e anche il nostro. Ciò che, invece, è al di là della circonferenza-spazio rappresenta il futuro. Esso sarà occupato domani dal nuovo spazio che corrisponde al tempo domani.

Insomma, considerare come spazio TUTTO il palloncino che si gonfia è un errore fondamentale. Esso rappresenta un mix di spazio e tempo. Le stelle, le galassie, i pianeti stanno OGGI tutti su una sola circonferenza, una linea curva, o su una superficie sferica. In realtà, dato che le dimensioni dello spazio sono tre, stanno in uno spazio a tre dimensioni istantaneo, impossibile da disegnare senza tralasciare il tempo che scorre.

Ben diverso è, invece, ciò che potremmo vedere OGGI.

Per comprendere questo punto fondamentale, dobbiamo occuparci del cammino della luce in una figura che vede ogni stella con il suo tempo e con uno spazio circolare, in quel dato istante.

La Fig. 15 dovrebbe essere ampiamente esplicativa anche se estremamente “rozza”.

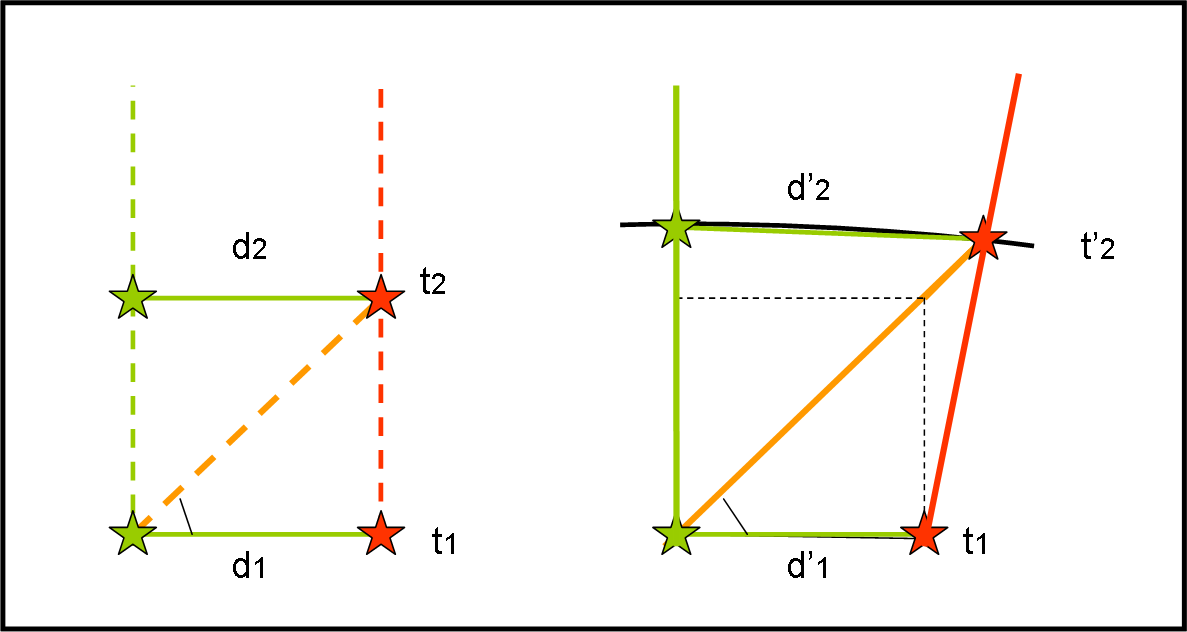
Seguiamola con attenzione. A sinistra abbiamo il nostro Universo statico, senza espansione. La luce della stella azzurra, partita al tempo t₁, raggiunge la stella rossa al tempo t₂. Basta, infatti, tracciare un segmento a 45° rispetto agli assi dello spazio e del tempo e ricavare subito l’istante in cui la luce arriva alla stella rossa. Notiamo che la distanza tra le stelle è rimasta immutata. Essa è anche la distanza percorsa dalla luce nel tempo t₂ – t₁.

Riprendiamo le nostre stelle allo stesso istante t₁. Manteniamo verticale la linea di Universo della stella verde (possiamo farlo benissimo). La linea di Universo della stella rossa è, invece, inclinata, dato che l’Universo si espande e le due stelle seguono linee che si allontanano tra loro. Facciamo partire la luce dalla stella verde in t₁ (come prima). Essa è diretta a 45° rispetto alla verticale (la tangente alla circonferenza che indica lo spazio che coincide con la linea orizzontale).

Andiamo avanti finché la luce arriva sulla stella rossa. Cosa è successo rispetto a prima? Beh… è immediato vedere che la luce ha impiegato più tempo (t’2  > t2). Accidenti… ma la luce deve andare sempre alla stessa velocità, per cui deve avere percorso uno spazio più lungo. Ma… anche questo è vero! Infatti, d’₂ è superiore a d₂.

Lo spazio dovrebbe essere misurato lungo l’arco di circonferenza, ma la differenza è minima e possiamo considerare la corda che unisce le due stelle. Ne segue che la distanza tra le due stelle non è più una costante, ma varia col tempo. Quando la luce è partita era d₁ = d₁’, quando è arrivata è invece d’₂ > d₂ = d₁ = d’₁.

Abbiamo un bel problema… qual è la distanza tra le due stelle? La prima o la seconda? Dobbiamo scegliere e, comunque, avremmo sempre una distanza variabile. La luce, poverina, ha dovuto percorrere uno spazio più lungo, una via di mezzo tra d’₁ e d’₂.

In conclusione: la distanza tra due stelle varia da istante a istante: quella relativa alla partenza della luce NON è uguale a quella relativa all’arrivo della luce. In altre parole: quando la luce è partita le due stelle erano più vicine tra loro rispetto a quando la luce  arriva sulla seconda. La luce ha dovuto fare un percorso più lungo rispetto a quello dell’Universo statico.

Come già detto,  la rappresentazione è un po’ “rozza”…

Quando la luce arriva sulla stella rossa, essa dovrebbe arrivarci formando sempre un angolo di 45° con la linea di Universo della stella rossa. La nostra approssimazione brutale non ne tiene conto. In realtà la luce non compie un percorso spazio-temporale rettilineo, ma curva continuamente in modo da presentarsi alla stella rossa con l’angolo giusto e al tempo giusto (leggermente inferiore a quello disegnato). Per tracciare, quindi, percorsi molto lunghi della luce è necessario fare dei passi molto piccoli, in modo da eliminare al massimo il problema sopra accennato.

La Fig. 16 mostra un sistema per migliorare la costruzione (anche se apparentemente sembra la stessa cosa).

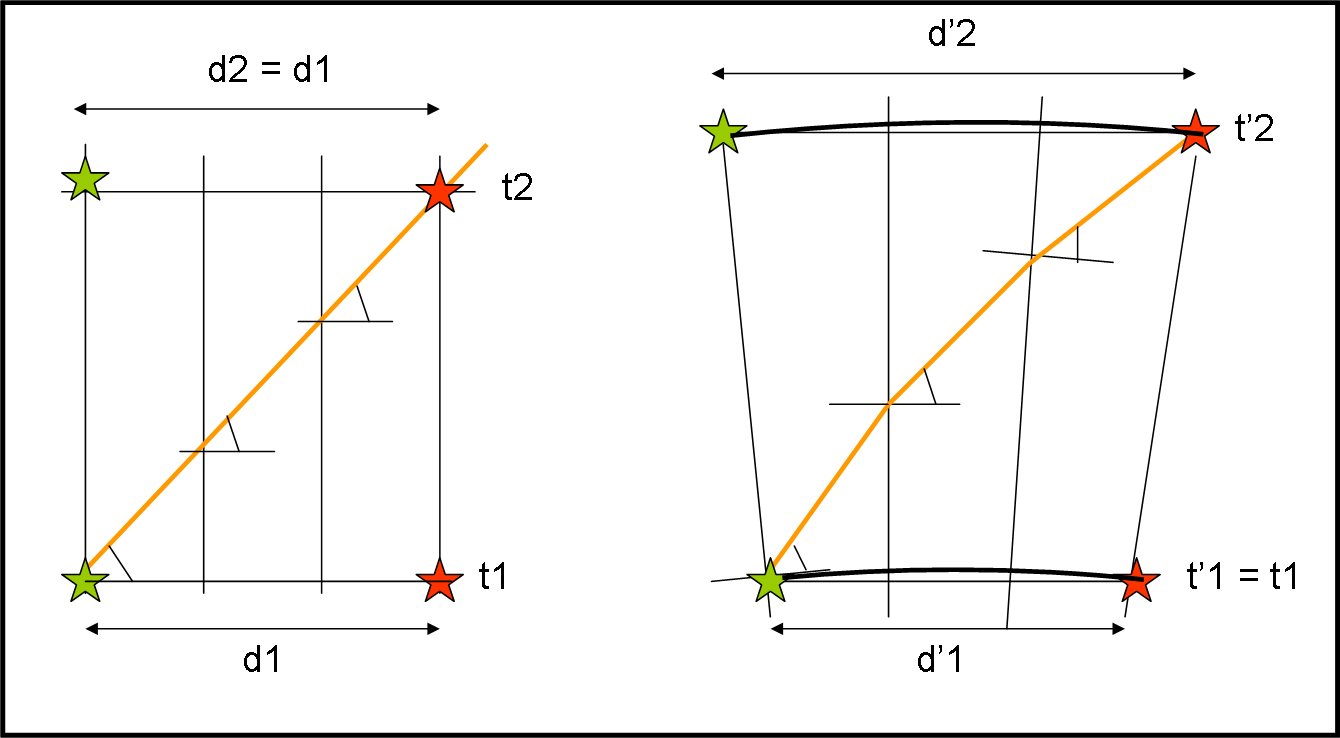
Tra le due stelle si considerano tante linee di Universo “ausiliarie”, tali che la loro distanza sia realmente infinitesima. Noi ne abbiamo considerate solo due per semplicità. Si ripete la costruzione di prima, aggiornando la direzione della luce ad ogni incontro. Ne viene fuori una linea spezzata che per intervalli estremamente piccoli tende a essere una curva continua, com’è in realtà.

Utilizzando questa procedura si può costruire il percorso della luce per periodi di tempo anche molto lunghi. Addirittura come l’età dell’Universo, immaginando la luce partita all’istante del Big Bang. In realtà, sappiamo che la prima luce dell’Universo è stata “lanciata” dopo 380 000 anni, al momento della radiazione cosmica di fondo.

Lo vediamo in Fig. 17 (abbiamo esagerato volontariamente l’intervallo temporale in cui nessuna luce poteva uscire dallo spazio che si espandeva al passare del tempo, che coincide con il cerchio arancione).

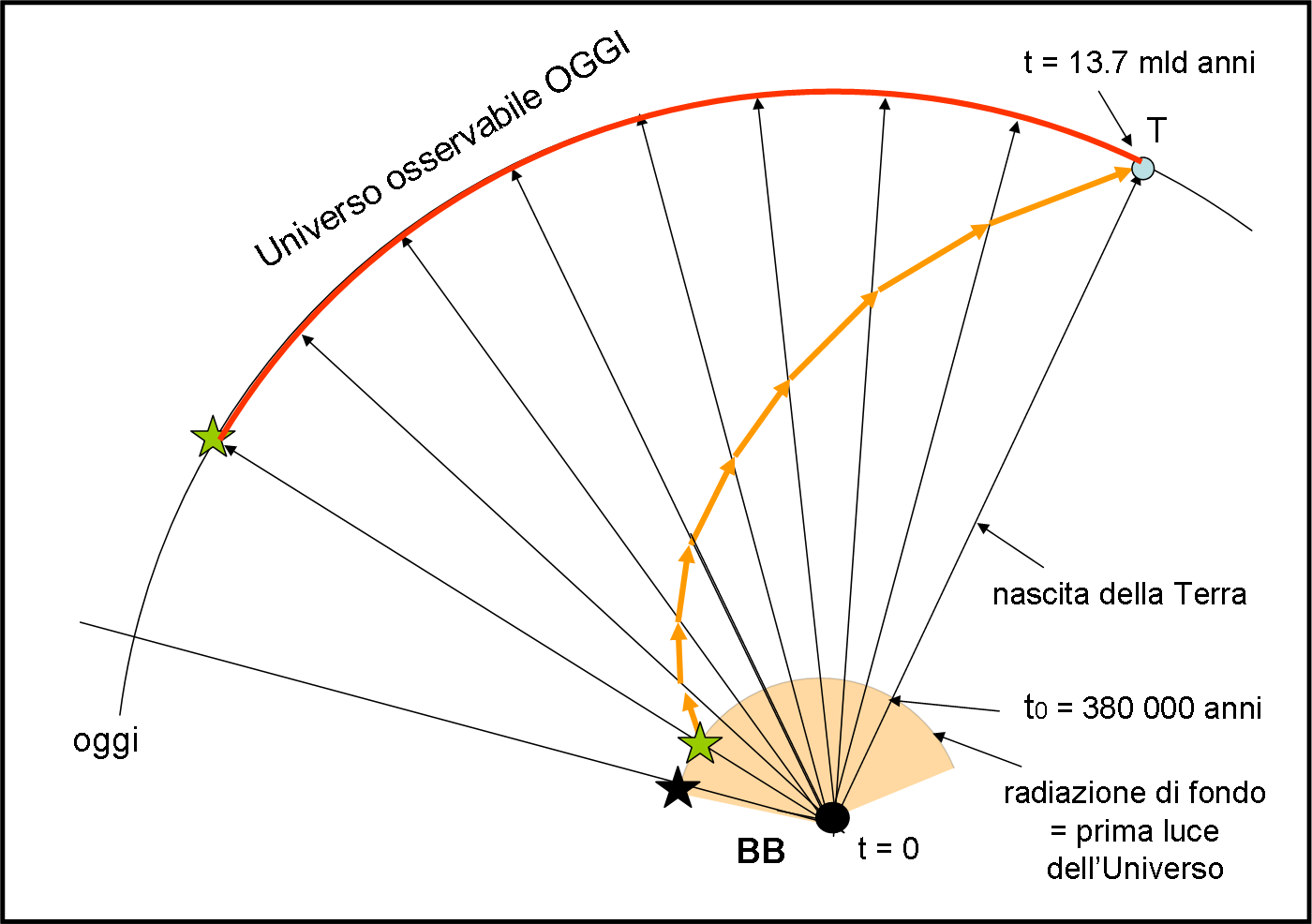
La radiazione cosmica di fondo non è veramente la luce di una stella, dato che le stelle dovevano ancora formarsi. E’tuttavia, qualcosa che si può "vedere", in quanto luce, e noi la indichiamo come stelle per semplicità. Oggi ci sta raggiungendo quella della “stella” verde, dopo il cerchio arancione (di quel periodo non possiamo avere informazioni, almeno per adesso) ed è in assoluto la luce della “cosa “ più antica visibile oggi. La luce della “stella” nera arriverà, invece, solo “domani” (sarà comunque sempre radiazione di fondo).

La luce percorre il suo tracciato curvilineo e arriva finalmente alla Terra all’istante OGGI. La distanza originaria tra la Terra (o quello che c’era prima di lei) e la stella era relativamente piccola al momento dell’invio della luce (bordo del cerchio arancione), ma adesso è diventata veramente gigantesca. Ovviamente, la Terra potrebbe anche essere nata molto dopo la partenza della luce dalla stella, ma poco importa. Ciò che conta è che oggi la riesca a ricevere. Se la stella-radiazione di fondo rappresenta la cosa più distante tra quelle che teoricamente potremmo ricevere OGGI, definiamo come Universo Osservabile (anzi ½ Universo Osservabile) la distanza tra la stella OGGI e la Terra OGGI, come fatto nel caso dell’Universo statico.

Risulta subito evidente la spiegazione di ciò che mette in agitazione molti curiosi, poco preparati. Essi dicono: “Ma come è possibile che possa esistere una stella la cui distanza in anni luce sia maggiore dell’età dell’Universo?”. Bene la figura lo dimostra senza creare alcun problema…

L’espansione dell’Universo ha trascinato la stella a una distanza da noi (misurata nello spazio di oggi) che può essere di gran lunga maggiore di quanto la luce riesca a percorrere in 13.7 miliardi di anni, senza subire l’espansione dell’Universo. Oggi l’Universo Osservabile si aggira intorno ai 90 miliardi di anni luce (in diametro), ma molto dipende dal modello cosmologico usato.

Come al solito, DOMANI l’Universo Osservabile si ingrandirà, dato che ci raggiungerà anche la luce della stella nera. Quello di ieri era invece più piccolo. Analogamente a quanto fatto nella Fig. 10, possiamo disegnare la Fig. 18, dove si vede come era l’Universo Osservabile nel passato.

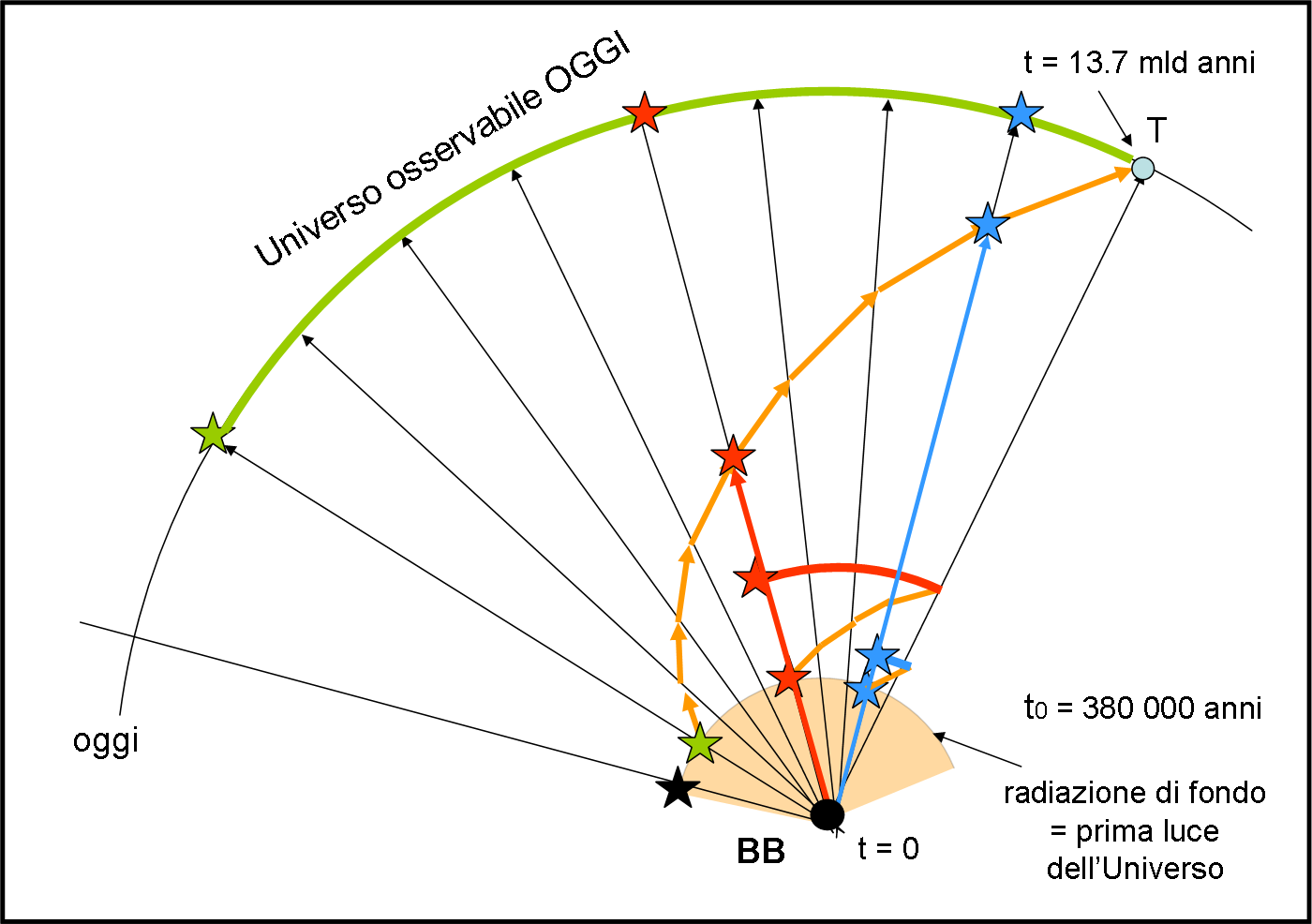
In particolare, vediamo quello relativo al tempo in cui la luce della stella rossa ne segnava il limite (curva rossa) e, ancora più piccolo, quello relativo al tempo in cui era la stella blu a segnarne il limite (curva blu). Ovviamente la luce delle stelle rossa e blu giunge a noi anche oggi, ma essa è partita in tempi molto più recenti.

Come nel caso dell’Universo statico, tutte le stelle la cui luce arriva sulla terra OGGI devono stare sulla curva curvilinea della luce. Ma, ancora una volta, questo succede perché lavoriamo con uno spazio a una dimensione. Se lavorassimo con due dimensioni quella strana curva diventerebbe una specie di cono che si apre e si richiude. Non per niente esso rappresenta il Cono di Luce passato della Terra, ossia quello che contiene tutto ciò la cui luce ha raggiunto la Terra fino a OGGI.

In teoria, potremmo anche disegnare il cono di luce fino a farlo arrivare al Big Bang, ma la costruzione sarebbe piuttosto confusa. D’altra parte dalla zona rosa non può essere uscita alcuna luce.

Sicuramente, però, tutti i coni di luce devono e possono arrivare teoricamente fino al Big Bang, dato che tutto ciò che esiste è nato lì. In qualsiasi istante dell’esistenza passata della Terra sarebbe giunta la sua luce. Se la potessimo vedere, essa sarebbe, quindi, ovunque, in qualsiasi direzione guardassimo, dato che al tempo t = 0 esisteva solo lui e rappresentava tutto l’Universo. Il nostro palloncino doveva ancora gonfiarsi...

Ma non complichiamoci le cose. Abbiamo già in mano molte chiavi per aprire il teatro dell’Universo.

Altre figure, decisamente meno immediate, potrebbero mantenere l'asse dello spazio rettilineo o cose del genere, ma dovrebbero essere introdotte coordinate particolari che , al momento, è meglio tralasciare.

Concludiamo, pensando alla fantastica luce e al suo percorso ben più lungo di quanto si potesse pensare. In qualche modo è come se lei cercasse di venirci incontro nel modo più rapido, ma lo spazio davanti a lei aumenta continuamente ed è costretta a navigare, trascinata in senso opposto dall’espansione.

Oltretutto, l’espansione può anche dare luogo a stelle dell’Universo Osservabile odierno, che si allontanino da noi più velocemente della luce (perché, come abbiamo già spiegato, la velocità di espansione dell'Universo può superare quella della luce) e quindi essa, invece di venire verso di noi, anche se con grande fatica (pensiamo, per esempio, a quel piccolo fotone che ha compiuto un viaggio di 7,5 miliardi di anni e ce lo ha raccontato), verrebbe rimandata indietro e allontanata. Il fotone cercherebbe di raggiungerci, ma sarebbe trascinato lontano dall’espansione. Poverino… è come se salisse di un metro, ma ne scendesse due!

In qualche modo, vi è anche un limite che nega alla luce delle stelle del nostro Universo osservabile di raggiungerci. Una specie di orizzonte degli eventi, come quello dei buchi neri… Nessuna informazione potrebbe essere scambiata con chi sta fuori da questa… siepe. Sì, un’altra siepe ancora, che ci nega di conoscere l’intero Universo, e ci costringe nel nostro “piccolo” Universo di … provincia.

Attenzione! Ripetiamo ancora di non confondere Universo Osservabile con Universo Osservato. L’Universo Osservabile  corrisponde alla posizione attuale di tutto ciò la cui luce ci raggiunge oggi. L’Universo Osservabile è del tutto estraneo alle nostre capacità: la cosa più lontana la cui luce ci ha raggiunto è indipendente da ciò che noi riusciamo a vedere.

L’Universo Osservato sarebbe teoricamente la stessa cosa, ma il numero dei suoi oggetti celesti dipende da come noi siamo capaci a rilevare la loro luce. La luce di molti oggetti che arriva da noi oggi è troppo debole per essere realmente "osservata" e gli oggetti restano del tutto sconosciuti a causa dei limiti tecnologici degli strumenti a disposizione.  Possiamo, però, dire che l’uomo è riuscito a osservare direttamente il limite dell’Universo Osservabile, dato che riesce a leggere la radiazione cosmica di fondo, la prima luce della cosa più distante osservabile oggi.

A questo punto appare già chiaro che il tempo che la luce impiega a viaggiare da un corpo celeste ad un altro non può essere assunto come misura della distanza tra i due corpi. Riteniamo, tuttavia, utile approfondire la trattazione di questo punto, data la sua importanza.

 

Distanze e velocità della luce: Universo statico * 

Innanzitutto, vediamo di definire la distanza tra due oggetti. Sul nostro pianeta è molto semplice. Bastano due dita, un righello, o altri ben noti accorgimenti per valutare la separazione spaziale tra due corpi, sia direttamente che su una cartina geografica. Il procedimento diventa addirittura banale quando gli oggetti sono immobili e la distanza fissa. Leggermente più complicata è la misura della distanza tra due corpi che siano in movimento, ad esempio due automobili lungo un’autostrada. In questo caso è fondamentale conoscere la legge del moto di uno rispetto all’altro e poi procedere al calcolo della distanza che è valida istante per istante e varia in funzione del tempo. Se non si ha la legge del moto, si può agire attraverso triangolazioni effettuate da osservatori posti in posizioni diverse o in grado di “vedere” il movimento da una distanza considerevole (satelliti artificiali).

Tuttavia, abbiamo già fatto un passaggio enorme. Se misuro direttamente la distanza tra due oggetti allo stesso tempo t sono sicuro che quella sia la distanza vera. Se, invece misuro la distanza attraverso osservazioni di due oggetti posti  lontano uno dall'altro, dovrei tener conto che la luce proveniente da uno dei due oggetti è partita prima dell'altra e ha quindi impiegato meno tempo per giungere a me. In realtà sulla Terra ciò non ha importanza vista la limitatezza delle distanze rispetto alla velocità della luce.

Lo stesso procedimento viene usato per determinare le distanze nel Sistema Solare, dove è nota, sia attraverso la teoria che attraverso modelli al computer, la legge del moto di un corpo attorno a un altro. Quanto ciò sia valido viene dimostrato quotidianamente dalle missioni spaziali in cui le distanze relative tra i corpi in gioco sono conosciute a priori e proprio sulla loro precisione ci si affida per guidare l’intero viaggio di una sonda (e il successo di missioni come Cassini, New Horizons, Dawn e Juno - solo per fare alcuni esempi - ne costituisce la conferma). Tuttavia, quando si eseguono le osservazioni necessarie allo scopo non è più possibile trascurare il tempo diverso che la luce impiega per giungere fino a noi. In qualche modo si esegue una correzione per il tempo luce (lo facevamo sempre, ad esempio, quando si osservava la curva di luce di un asteroide, dovendo tenere presente che l'oggetto si allontanava o si avvicinava da noi durante la durata delle osservazioni. Conoscendo la distanza istante per istante dalla legge del moto si poteva correggere il tempo a cui riferire la singola osservazione, come ho spiegato QUI)

Le cose si complicano quando si esce dal Sistema Solare. Il metodo sicuramente più semplice si affida alla ben nota parallasse annua. Esso può essere applicato solo a stelle relativamente vicine, tali che esse riescano a “vedere” il movimento della Terra attorno al Sole. In realtà, il nostro movimento reale si riflette in un movimento apparente delle stelle che descrivono durante un anno una piccola ellisse che permette di passare alla misura lineare della distanza da noi (si osserva un angolo e si misura un lato di un triangolo rettangolo). In questo caso, ovviamente, si considera la stella immobile rispetto alla Terra durante l'anno necessario all'osservazione: l'errore introdotto nel non tener conto di piccoli cambiamenti di distanza è trascurabile, vista la distanza della stella, relativamente piccola su scala cosmica, infatti il metodo della parallasse è utilizzabile solo per stelle non più distanti di 100 anni luce (per comprendere quanto sia "piccola" tale distanza, si consideri che solo la nostra Via Lattea ha un diametro di circa 100 000 anni luce).

Da questo punto in poi, il movimento del nostro pianeta diventa troppo piccolo e l’unica risposta può provenire dalla luce e dalle caratteristiche peculiari di chi emette la luce. Infatti, i moti degli astri sono in gran parte casuali (a parte la comune rotazione attorno al centro della galassia) e non riproducibili con formule. Abbiamo così il procedimento basato sulla variabilità periodica delle cefeidi e la costanza della luminosità assoluta delle supernove di tipo Ia (ma su di esse si sta facendo strada qualche dubbio...)

Senza entrare nei dettagli, però, si deve ricordare sempre che la velocità della luce, malgrado sia la massima raggiungibile in natura, è comunque finita e impiega un certo tempo per giungere fino a noi.

La distanza che misuriamo è quindi quella tra la posizione dell’oggetto S1 al momento t1, in cui è stata emessa la luce, e la nostra posizione quando la riceviamo (che possiamo supporre sempre la stessa), al tempo t2. Se la stella non si fosse mossa, questa distanza sarebbe sempre la stessa. Se invece la stella ha un moto relativo rispetto a noi (escludendo l’espansione dell’Universo), allora la distanza calcolata sulla base della luce ricevuta oggi, sarebbe diversa da quella che la stella ha realmente oggi. Comunque sia, non si commettono errori significativi quando la distanza tra una stella al tempo t1 e noi viene espressa in anni luce, ossia in termini di distanza percorsa dalla luce, emessa dalla stella al tempo t1, per giungere fino a noi.  I movimenti reciproci delle stelle sono decisamente trascurabili rispetto ai tempi di vita umani.

Avete notato che finora non abbiamo parlato di espansione dell'Universo, ma solo di distanze tra oggetti che mantengono sempre la stessa distanza su tempi molto lunghi o, al più, eseguono movimenti reciproci estremamente ridotti. Essi si muovono in uno spazio che non cambia (e tale può essere considerato, compiendo errori di misura trascurabili, lo spazio entro un raggio di due miliardi di anni luce).

 

Distanze e velocità della luce: Universo in espansione ** 

Attenzione, però, che ciò è possibile se i fotoni che hanno lasciato la stella hanno potuto viaggiare senza alcun intoppo. Infatti, se il tempo necessario alla luce per coprire una certa distanza fosse di 57 anni, ma essa si fermasse a fare uno “spuntino” da qualche parte per una ventina d’anni per poi riprendere il viaggio, la nostra misura finale di 77 anni sarebbe errata, a meno di non venire a conoscenza della sosta e quindi di potere tenerne conto sottraendola al valore finale.

Purtroppo, i fotoni non parlano e non ci diranno mai se sono fermati da qualche parte o quantomeno se hanno rallentato. In realtà i fotoni non rallentano e nemmeno si fermano a mangiare (al limite si affievoliscono). La loro velocità è costante e teoricamente senza intoppi. Ma è lo spazio che devono percorrere che può giocare loro degli scherzi, quando il gioco si fa duro, ossia quando il tempo impiegato dalla luce è veramente MOLTO lungo. L’espansione dell’Universo non può più essere trascurata e, anzi, è proprio lei che determina il tipo di distanza che possiamo ottenere.

Se esso si “ingrandisse” notevolmente, i fotoni dovrebbero percorrere una distanza maggiore di quella preventivata. La misura della distanza, espressa in anni luce, avrebbe un significato diverso. Ci direbbe soltanto che la luce è partita al tempo t1, ossia un certo numero di anni fa, e ci ha raggiunto OGGI, ma non ci darebbe una misura corretta della distanza reale della stella al tempo t1, né di quella di OGGI. In altre parole, il numero di anni impiegati dalla luce a percorrere lo spazio tra la stella e noi poco avrebbe in comune con la vera distanza tra la galassia e noi. La situazione, quando si parla di distanze veramente grandi è, però, proprio questa ed è in perfetta sintonia con quanto visto nei capitoli precedenti.

Per riassumere, potremmo dire che le distanze misurate, senza intoppi da parte dei fotoni, sono quelle relative a uno spazio che può essere considerato immutabile, in cui gli oggetti si muovono soltanto per il loro moto proprio. Qualcosa di molto simile alle distanze misurate nella realtà di tutti i giorni. Se invece lo spazio non è immutabile, ma cambia costantemente, le distanze assumono significati diversi e più complessi.

Purtroppo, per distanze veramente grandi, maggiori di un paio di miliardi di anni luce, lo spazio non può approssimarsi come immobile, o meglio statico. Esso si espande continuamente e il percorso della luce compiuta in un certo periodo di tempo è ben maggiore di quello relativo alla differenza di tempo tra quando i fotoni sono stati emessi e OGGI. In altre parole, dire che una galassia è vecchia di 10 miliardi di anni è ancora esatto, ma dire che essa dista 10 miliardi anni luce da noi NON è più esatto. A questo punto dobbiamo farci aiutare dalla Fig. 19 (che ormai conosciamo abbastanza bene), in grado di sintetizzare e chiarire quanto detto finora e permettere di definire le distanze in uno spazio in espansione.

Come già sappiamo, lo spazio è considerato a una dimensione ed è rappresentato dalle conferenze concentriche che si allargano sempre più a causa dell’espansione dell’Universo. Il tempo scorre invece in senso radiale. La posizione della Terra è rappresentata dalla sferetta blu e l’asse orizzontale descrive il nostro tempo (NON è una posizione privilegiata, dato che qualsiasi retta che parta dal Big Bang può essere considerata asse delle ascisse). Lo spazio invece varia da momento a momento e le distanze possono essere misurate solo su queste circonferenze.

Se non ci fosse espansione e potessimo bloccare lo spazio (ad esempio quello relativo a 4 miliardi di anni dopo il Big Bang), tutte le misure di distanza, se possibili, sarebbero senza ambiguità e si ricondurrebbero ai metodi accennati precedentemente. Purtroppo (o per fortuna?) lo spazio, invece, si espande.

Sappiamo anche che la linea curva, che parte dal Big Bang e giunge fino a noi, rappresenta il CONO DI LUCE relativo al nostro passato, ossia tutto ciò che noi riusciamo a vedere oggi. Per il momento tralasciamo i numeri scritti vicino al CONO DI LUCE: ci torneremo tra poco.

Se non ci fosse espansione, la luce ci raggiungerebbe senza “intoppi” e la distanza tra la galassia e noi sarebbe uguale all’arco di cerchio marrone tra le sferette gialla e blu. Potrebbe essere espressa correttamente in anni luce, ossia in spazio percorso dalla luce per andare dalla sferetta gialla a quella blu. Purtroppo, però, mentre la luce tenta di descrivere il tratto marrone, lo spazio si è espanso e dopo un miliardo di anni è diventato una circonferenza con un raggio maggiore. La luce è costretta, quindi, a viaggiare anche in senso radiale rispetto al Big Bang. Come conseguenza il suo moto sarà spaziotemporale, dato che lo spazio dipende direttamente dal tempo a causa dell’espansione.

Qual è allora la vera distanza percorsa dalla luce? Non è ovvio rispondere, come potete facilmente vedere. La traiettoria descritta è spaziotemporale, ma la distanza deve essere misurata nello spazio (ossia, lungo una circonferenza). Sì, ma quale? Quello di 4 miliardi di anni dopo il Big Bang (arco nero) o quello di oggi (arco viola)? Entrambe sono giuste, ma differiscono di molti anni luce tra loro. Forse sarebbe meglio usare un valore medio? No, no, sarebbe comunque sbagliato.

Molto meglio, allora, calcolare entrambe le distanze e chiamarle per nome, in funzione del tempo: d_E, al momento t = 4 miliardi di anni dopo il Big Bang, quando la luce è stata emessa (arco marrone) e d_A, al momento t = 14 miliardi di anni, ossia quella attuale. Esse sono distanze reali, misurabili in anni luce, ma estremamente diverse tra loro, a causa dell’espansione.

Tuttavia, le relazioni esistenti tra queste distanze, in funzione del tempo e del tipo di espansione prescelto, possono essere calcolate.

La distanza di una galassia espressa in anni luce non ha più  senso. OGGI la galassia gialla disterà da noi più dei 10 miliardi di anni, cui generalmente ci si riferisce quando si danno i risultati di oggetti ultra lontani. Dire, ad esempio, che la radiazione cosmica di fondo dista da noi poco meno di 14 miliardi di anni (o che lo stesso Big Bang dista 14 miliardi di anni) è in realtà un errore. E’ invece giusto dire che la sua età è di 14 miliardi di anni o meglio che la luce emessa (e che oggi ci raggiunge) è partita 14 miliardi di anni fa. Un errore comunissimo, veniale se vogliamo, ma che spesso getta grande confusione nella comprensione dello spazio-tempo. Ovviamente, i professionisti sanno benissimo a cosa ci si riferisce e come trasformare quel dato in distanze reali. Ma per i non addetti ai lavori, la cosa può dare luogo ad ambiguità.

Vale la pena ricordare come si determinano le distanze di oggetti, lontanissimi nel tempo, attraverso la legge di Hubble. Essa, in modo molto semplice, dice che esiste una relazione tra la velocità di espansione dell’Universo (o meglio ancora di allontanamento tra le galassie) e distanza dell’oggetto celeste. La relazione è lineare e vale semplicemente d = Ho ∙ v, dove d è la distanza, v è la velocità di allontanamento e Ho è una costante. Tuttavia, Ho è una costante variabile, in quanto assume valori sempre diversi in tempi diversi (rappresenta in pratica le modalità dell’espansione).

Essa è una costante per un tempo ben determinato, nel senso che è uguale per tutto l’Universo all’istante t. Ne consegue che essa fornisce un valore diverso della distanza a seconda del tempo e quindi della costante che noi inseriamo. Questo fatto ci porta a una conclusione importantissima. Il valore più importante è quello realmente osservato della velocità di allontanamento, ottenuto attraverso il redshift z (spostamento delle righe spettrali verso il rosso). A partire da questa velocità è possibile, attraverso formule più o meno complicate, calcolare le distanza che preferiamo. E’ giusto quindi inserire sul CONO DI LUCE i valori del redshift z per i vari tempi a partire dal Big Bang, come fatto in Fig. 19. Ricordiamo brevemente che il redshift si misura direttamente guardando di quanto una certa riga dello spettro elettromagnatico si è spostata verso il rosso (lunghezza d'onda più lunga) rispetto a ciò che si osserva in laboratorio. 

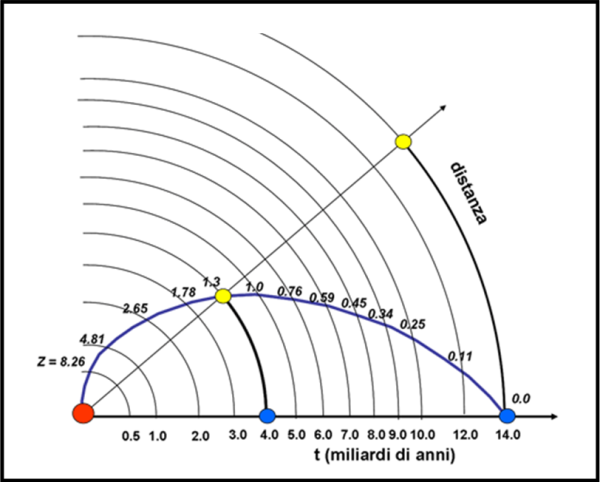
Essi ci forniscono le velocità che sono strettamente legate alle distanze che vogliamo considerare. La formula (banale) che lega le distanze prima definite e il redshift è la seguente: d_E= d_A/ ( 1 + z ). Ne segue che 1/(1 + z) è un vero e proprio fattore di riduzione che ci permette di risalire alle vere distanze al momento dell’emissione della luce, in funzione del redshift osservato. Ovviamente, il suo inverso (1 + z) permette di passare dalla distanza di emissione a quella attuale ed è il fattore di espansione dell’Universo.

Essendo il valore di z legato strettamente al tempo di emissione, esso si usa per stabilire l’età dell’emissione della luce da parte dell’oggetto (concetto esatto) o la distanza in anni luce (non esatta, ma facilmente riconducibile alle distanze reali). Questa situazione porta, però, a incomprensioni. Si dice, ad esempio, che il Big Bang ha un’età di circa 14 miliardi di anni (esatto), ma si dice anche che esso dista 14 miliardi di anni luce (errato). E’ invece vero che l’Universo Osservabile ha un raggio di circa 47 miliardi di anni luce. Com’è possibile che vi siano oggetti più distanti del Big Bang? Tutto torna perfettamente se teniamo conto di quanto ho cercato di esprimere precedentemente (spero, almeno…).

Come già accennato, per oggetti più vicini di circa un paio di miliardi di anni (temporalmente), i problemi sollevati possono essere “praticamente” trascurati, in quanto l’espansione non ha causato grandi differenze (il più delle volte nei limiti della precisione delle misure).

A questo punto, possiamo concludere descrivendo le distanze principali che si usano nell’Universo e la loro definizione. Esse sono quattro:

1) Distanza comovente (d_C). Essa indica la distanza che si espande con l’Universo. In altre parole, essa dice dove si trovano le varie galassie OGGI, anche se la luce era partita da loro quando l’Universo era ben più piccolo e le distanze minori. Essa è uguale alla nostra d_A. Con questa definizione l’Universo osservabile ha un raggio pari a 47 miliardi di anni luce, mentre le galassie più lontane visibili con il telescopio Spaziale Hubble hanno una distanza di circa 32 miliardi di anni luce (questa differenza vuole solo dire che non abbiamo ancora osservato con Hubble TUTTO l'Universo osservabile: la luce è arrivata, ma era troppo debole per lo strumento). La distanza comovente può anche essere considerata una costante in un sistema di riferimento che tenga conto intrinsecamente del fattore di espansione (1 + z), dato che la sua variazione dipende solo da tale fattore.

2) Distanza di diametro angolare (d_A). Noi vediamo oggi le galassie com’erano al momento in cui ci hanno inviato la luce. In quel momento sappiamo benissimo che la distanza (d_E) era minore di quella che è oggi. Le dimensioni della galassia che vediamo oggi sono relative, però, a quel ben determinato istante. In altre parole, le dimensioni della galassia sono ben più grandi di quanto ci si aspetterebbe da un oggetto così lontano. In altre parole ancora, il diametro angolare di una galassia si conserva attraverso l’espansione (l’espansione espande lo spazio, non i singoli oggetti). Ne consegue che il diametro angolare che vediamo oggi è strettamente legato alla distanza della galassia al momento dell’emissione della luce (d_E). Questo tipo di distanza è in pratica la distanza al momento dell’emissione della luce.

3) Distanza di luminosità (d_L). Durante l’espansione, la luce che arriva fino a noi è molto più debole di quanto indicherebbe la distanza che la galassia aveva al momento dell’emissione della luce. Ciò è causato dalla dispersione della luce su una superficie più vasta. Ne consegue che le galassie più lontane osservate dal telescopio Spaziale appaiono come se si trovassero a distanze di circa 350 miliardi di anni luce. Ovviamente essa non è una misura realistica, ma è utile per determinare il fattore di affievolimento della luce.

4) Distanza di tempo luce (d_T). Essa rappresenta il tempo impiegato dalla luce di una galassia per giungere fino a noi. Questa definizione è quella che ci permette di dire che il Big Bang è “distante” circa 14 miliardi di anni luce. Essa è però, in realtà, una misura di tempo e non di distanza. In pratica si ottiene semplicemente moltiplicando l’età di un evento per la velocità della luce.

L’andamento di queste quattro distanze in funzione del redshift z è riportato in Fig. 20. Per come sono state definite è abbastanza ovvio che per oggetti relativamente vicini a noi (redshift minori di 0.1) e relativamente vicini nel tempo (un paio di miliardi di anni) le quattro distanza coincidono tra loro.

 

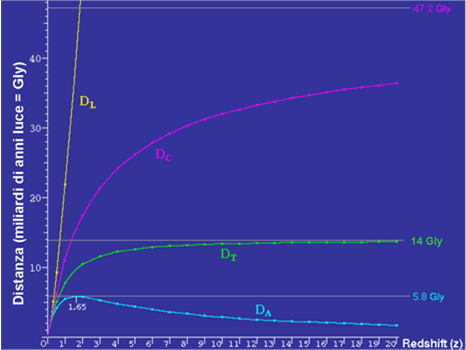
A questo punto siamo pronti per avvicinarci all'ultima frontiera dell'Universo... quella oltre la quale, nonostante i progressi tecnologici, sarà molto probabilmente impossibile guardare con altri occhi che non siano quelli della mente: la sfera di Hubble.

 

NEWS!! - La legge di Hubble ha ufficialmente cambiato nome, d'ora in poi di chiamerà LEGGE di HUBBLE-LEMAITRE. Il motivo ve lo raccontiamo QUI

Per arricchire la comprensione di “siepi” e “ultimi orizzonti”, QUI avete a disposizione il più illustre esperto in materia…