Categorie: Fisica classica
Tags: accelerazione di gravità caduta libera forza peso jerk resistenza aerodinamica
Scritto da: Maurizio Bernardi
Commenti:15
Un, due, tre... Jerk ! **
Questo articolo è stato inserito nella pagina d'archivio "Dinamica e meccanica", compresa in "Fisica classica"
Chi non ha mai viaggiato in treno o in automobile? Tanto basta per capire i "fondamentali" del Jerk.
E di questo abbiamo parlato nei precedenti articoli sull'argomento (QUI e QUI). Ma ci sono esperienze molto meno comuni che fanno definitivamente amare questa derivata terza dello spazio, dal curioso nome.
Un, due, tre… Jerk!
Il paracadute, come la mente, funziona solo se si apre, ormai lo sappiamo bene.

Ma come funziona?
In realtà non basta che si apra, è bene che ci sia anche un po' di aria attorno, per tutta la discesa.
Se sulla Luna vi lanciate da 500 metri, il paracadute vi aiuterà poco. Vero è che l'accelerazione di gravità è solo un sesto di quella terrestre, quindi la velocità di impatto risulterà ridotta al 40 %, ma anche così, cadendo da 500 metri, senza atmosfera, arriverete al suolo con il paracadute chiuso, alla bella velocità di 40 m/s che se vi sembrano pochi, corrispondono a 110 km/h.
Sulla Terra va molto meglio. Con il paracadute non verrete giù come un sasso e, grazie alla presenza dell'aria, arriverete al suolo a 4 m/s , come se saltaste giù dal tavolo, invece che ai 100 m/s, pari a 360 km/h, di un salto senza paracadute.

Ma come avviene questo miracolo?
Non vi proponiamo una discussione a colpi di equazioni differenziali, tenendo conto di tutte le variabili, ma solo uno schema generale con qualche calcolo approssimato, giusto per dare una idea.
Una persona di 90 kg che volesse lanciarsi da 500 metri dovrebbe munirsi di un paracadute (è solo un esempio, senza voler fare pubblicità) come il SET 10 della Strong Enterprise , un paracadute emisferico, a calotta, con un raggio di 4,7m , una superficie di resistenza di 72 m2 ed un Cr, coefficiente di resistenza aerodinamica, di 1,28, un numero puro che conoscete dal gergo automobilistico con il nome di CX e che misura la forza che si oppone al movimento di un corpo in un fluido: il coefficiente di penetrazione.
Questo coefficiente è legato alla forma dell'oggetto in movimento: per un cubo vale circa 1, per una sfera 0,47, per un proiettile 0,04, per una Ferrari di F1 0,7, per la vostra utilitaria 0,35.
Come...? Il CX di una Ferrari è doppio di quello di una utilitaria?
Sì, avete per caso dato uno sguardo alle ruote? Come pensate che quei cilindroni possano penetrare facilmente nell'aria? E lasciamo perdere le turbolenze che si creano intorno...
Insomma, il martello e la piuma hanno CX diversi e se c'è la giusta atmosfera... cadono a velocità diverse (in assenza di atmosfera, invece, cadono alla stessa velocità, così come aveva intuito Galileo e come hanno verificato gli astronauti sulla Luna)
Tornando al paracadute, il coefficiente deve essere piuttosto alto, se no penetra facilmente nell'aria e non vi serve a niente.
Il paracadute emisferico è nato per frenare la caduta: ingabbia l'aria nella calotta e la comprime fino a creare una superficie fluida orizzontale. Questo genera una forza frenante che si oppone alla forza prodotta sulla massa dalla accelerazione di gravità.
Detto in formule, da un lato abbiamo la Forza Peso = mg, della massa che sta cadendo (90Kg) con accelerazione 9,81 m/s2
Dall'altro la forza frenante , detta Resistenza Aerodinamica = R, che si oppone alla caduta e dipende da:
Cr = coefficiente di resistenza aerodinamica (penetrazione)
= densità dell'aria che varia in funzione della pressione atmosferica e della temperatura, che assumeremo avere un valore medio di circa 1,2 Kg/m3
A = area della superficie esposta all'aria
v = velocità del corpo
L'espressione che lega questi parametri è la seguente:
R =
Una volta aperto il paracadute, la trasformazione del moto da rettilineo uniformemente accelerato, MRUA , a rettilineo uniforme, MRU, si completerà nell'istante in cui la velocità di caduta avrà raggiunto un valore tale per cui le due forze opposte (peso e resistenza aerodinamica) si bilanciano
mg =
Da questa espressione possiamo ricavare la velocità limite v
v = =
=
Questa sarà la velocità di discesa dopo il transitorio e si manterrà costante fino al momento dell'atterraggio (in seguito la chiameremo Vf = velocità finale)
Ma cosa succede durante il transitorio? Quanto dura? Che velocità si raggiunge? Di quanto si scende prima che il paracadute si apra? E quanto ci vuole prima che la velocità si stabilizzi?
Calma ! Il paracadute è composto dalla fune di vincolo, agganciata al cavo statico dell'aereo, da una calotta inizialmente ripiegata e dalle funicelle che compongono il fascio funicolare.
La calotta, una volta estratta dalla fune di vincolo, si apre e ingabbia l'aria durante la discesa, producendo una forza di resistenza aerodinamica contrastante la forza peso, dovuta alla gravità, che fa precipitare il paracadutista.
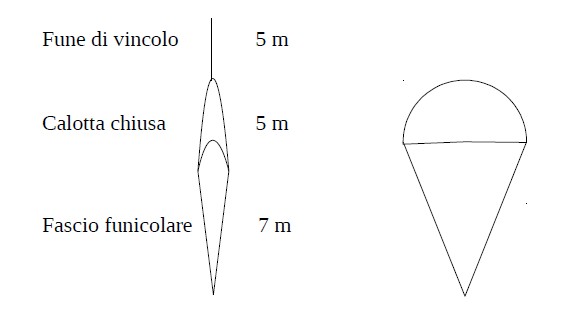
La fune di vincolo è agganciata all'aereo con una lunghezza di circa 5 metri (anche se circa 1 metro rimane all'interno dell'aereo), la sua azione è di sfilare la calotta la quale, ripiegata, è circa 5 metri e le funicelle lunghe 7 metri, dunque in totale 5+5+7=17 metri.
Fino allo svolgimento di tutti questi 17 metri siamo in caduta libera e non siamo sostenuti da nulla.
A questo punto il paracadute è completamente sfilato ma chiuso, si rompe la fettuccia sul foro apicale (apertura posta all’apice della calotta che, consentendo all'aria che vi è contenuta di sfuggire dalla sommità della stessa, assicura una discesa molto più stabile e regolare) e comincia l'apertura della calotta.
Occorreranno circa 2 secondi affinché la calotta sia completamente aperta e in questi 2 secondi avremo una frenatura parziale.
Non potendo stabilire a priori quanto sia la reale resistenza all'aria in questi ultimi 2 secondi, come considerazione logica potremo stabilire una media, considerando il primo secondo come caduta libera e il secondo successivo come se il paracadute fosse completamente aperto.
Per i primi 17 metri di caduta libera quanto tempo impiego?
secondi, che possiamo arrotondare a 2.
Abbiamo detto di considerare anche il secondo successivo in regime di caduta libera, quindi arriviamo a un totale di 3 secondi in caduta libera.
Quanto spazio ho percorso dopo 3 secondi e che velocità ho raggiunto?
Dopo 3 secondi di caduta sono sceso di 44 metri ed ho acquisito una velocità di quasi 30 m/s
La mia energia cinetica sarà:
Questa è la Energia iniziale.
Giungendo a terra alla velocità di 4 m/s, avrò una energia cinetica finale :
Il lavoro ( forza x spostamento) svolto per rallentare sarà uguale alla differenza tra la energie cinetiche: F*s = Ei-Ef da cui ricavo lo spazio
Ma quanto vale la forza F?
La calotta del paracadute, quando aperta, ingabbia l'aria che per sua natura possiede una certa massa, abbiamo visto che la sua densità è di circa 1,2 Kg per m3.
La calotta appena aperta è in caduta libera, quindi la massa d'aria sarà soggetta ad una accelerazione uguale a g. Se preferite, da un altro punto di vista, possiamo considerare la calotta ferma e la massa d'aria che la spinge verso l'alto.
Quanta aria è contenuta nella calotta? Proviamo a calcolare il volume come se fosse una semisfera,
tenendo conto che il raggio della calotta è all'incirca 4,7 metri:
Volume (semisfera) = 2/3 π r3
Dato che in 1 metro cubo ci sono 1,2 Kg di aria, la massa sarà: m=1,2 * 217 = 260 Kg Conseguentemene la forza sarà : F= 26*9,81 = 2550 Newton
La forza peso (che si mantiene costante) vale Peso = mg = 90*9,81 = 882,9 Newton
La forza frenante ha verso contrario alla forza peso, ma durante la frenatura, diminuendo la velocità, anche la forza frenante diminuirà progressivamente . Quindi potremo considerare un valore medio, al fine di calcolare lo spazio percorso nel transitorio:
F = (2550 -883)/2 = 833,5 N ( valore medio di forza che provoca la decelerazione)
Nota la forza, possiamo calcolare lo spazio percorso fino a quando la velocità costante:
S = (Ei-Ef)/F = (38976-720)/ 833,5 = 45,9 m (spazio per rallentare fino alla velocità costante)
In questi 46 metri avrò una decelerazione media di:
a= (Vf 2-Vi2)/2S = (42-29,432)/2*46 = -9,24 m/s2 (decelerazione media)
In quanto tempo coprirò lo spazio di 46 metri?
T=( Vf – Vi)/a = (4-29,43)/ -9,24 = 2.75 s ( tempo di rallentamento)
Abbiamo percorso fino ad ora 44 + 46 = 90 metri, e ci siamo stabilizzati ad una velocità di 4 m/s,
rimangono ancora 500 – 90 = 410 metri di discesa a velocità costante di 4 m/s.
Il tempo necessario per concludere la discesa sarà quindi
t=s/v = 410/4 = 102,5 secondi ( tempo rimanente all'atterraggio)
Riepiloghiamo la sequenza degli eventi in una tabella con relativo grafico:
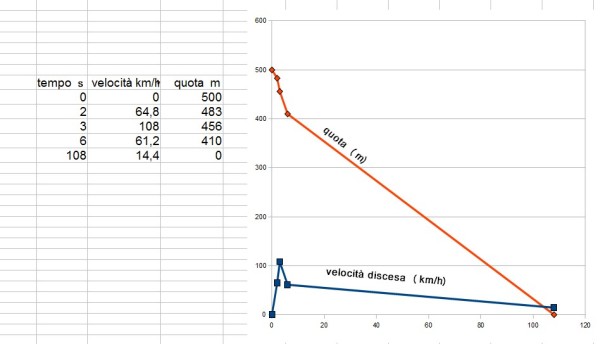
il picco di variazione di velocità ( curva blu) si manifesta all'istante del jerk
Dopo i primi 3 secondi la pendenza della linea della velocità passa da positiva a negativa, è in questo intervallo che la caduta libera (MRUA) si trasforma in caduta frenata (MRU).
La accelerazione antagonista fa la sua repentina comparsa e, come ormai sappiamo, questa variazione significa che si manifesterà lo strattone, causato dal Jerk, che prima era nullo ed improvvisamente è comparso come un impulso di durata breve ma di intensità significativa.
Da una accelerazione di 9,81 m/s2 si passa ad una accelerazione (9,81-9,24) = 0,57 m/s2.
Nel giro di un secondo o poco più, il jerk si manifesta con un differenziale di accelerazione che vale il 94% di g, in direzione opposta alla caduta.
Il paracadutista, avvertendo il jerk, ha quasi la sensazione di essere proiettato verso l'alto ( in realtà continua a cadere ma più lentamente). E' quello che viene definito come “shock di apertura”, e viene valutato come rapporto tra le due accelerazioni in conflitto. Nel caso visto il rapporto risulta -9,24/9,81 = -0,94
Si tratta di un calcolo su un valore medio della accelerazione frenante, dato che l'apertura avviene in modo graduale.
Ebbene, come abbiamo visto, non si ha il tempo di contare fino a tre, che arriva il Jerk.
Ma se il jerk tardasse anche solo un poco, certamente, questa volta, la cosa ci metterebbe una certa ansia.
Questo testo è una libera rielaborazione del documento “Discesa col paracadute emisferico” di Angelo Dei, reperibile in rete a questo indirizzo: www.anpdifirenze.it/documents/DiscesaConParacadute2.pdf
Per conoscere o approfondire le nozioni di fisica classica utilizzate in questo articolo, si consiglia la lettura de “La Fisica addormentata nel bosco”.






15 commenti
Con la "scusa" dello JERK,..... un bel ripassone di dinamica. Grazie !
Caro Franco, grazie per il tuo apprezzamento. Ricambio con una indiscrezione... È in arrivo la turbolenza ( ma mi raccomando, che resti tra noi)
OK !


Ottimo sistema per divulgare scienza, nello stile del blog. Sembra quasi di cadere nel vuoto mentre si riflette su cosa accadrebbe se il paracadute non si aprisse.
Attendo con ansia altre applicazioni pratiche.
Caro Giorgio, il tuo graditissimo commento mi spinge a perseverare.
Ebbene, conto di provarci, anche se sappiamo che perseverare è...diabolico.
Dare via libera al grande Mau è sempre molto pericoloso... ma è giusto... rischiare!

Caro Giorgio, tu non sai quanto fa piacere a tutti noi la tua frase: "Ottimo sistema per divulgare scienza, nello stile del blog". Una grande ricompensa per il modesto lavoro che cerchiamo di fare...
Maurizo, dato che sto andando un poco a rilento con con il libro del nostro Enzone, sai come si può calcolare l'aumento di pressione all'interno del paracadute? Il link all'anp non si apre e neppure la pagina principale del sito si apre. Thanks.
Caro Frank, scopro ora dal tuo commento questa inaccessibilità del sito. Mi auguro che si tratti di una situazione temporanea magari dovuta a manutenzioni o restyling.
In ogni caso nell'articolo citato non si entrava nel dettaglio che ti interessa.
Quello che posso dirti in prima battuta è che le variabili di cui tener conto nella realtà sono molteplici
Un tipico paracadute a calotta emisferica con apertura apicale e senza fenditure al suo interno ha una distribuzione di pressione variabile in funzione del diametro della sezione : la pressione diminuisce dove il diametro diminuisce (effetto Venturi) in modo che il prodotto della velocità di scorrimento del fluido per l'area della sezione si mantenga costante.
Si dovrebbero tenere in considerazione anche gli effetti della turbolenza sul bordo del foro di uscita apicale e la fuga di aria che si manifesta su tutta la ampia superficie per la porosità del tessuto, tipicamente nylon.
La sovra-pressione media all'interno della calotta è semplicemente il rapporto tra il peso di 90 chili da sostenere e la superficie della velatura di 72 mq , quindi circa 1,28 * 1,033 = 1,32 atmosfere. La pressione atmosferica esterna è però variabile in funzione della altitudine con una legge che vede all'esponente il rapporto metri/100: la formula è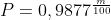
Ad esempio a 1000 metri la pressione atmosferica è circa l' 88% di quella a livello del mare e a 500 m (l'altezza del lancio descritto) è di circa 0,94 . Per la precisione ci sarebbe anche da considerare l'influenza sulla pressione di temperatura e umidità dell'aria, anche esse variabili con l'altitudine.
Se poi il paracadute è dotato di fenditure laterali , come quello della immagine in evidenza, che lasciano fuoriuscire aria per creare un moto trasversale di circa 2 m/s al fine di rendere pilotabile la discesa verso un obiettivo, le cose si complicano ulteriormente.
Insomma tutti questi ragionamenti per dirti che la tua domanda non può trovare una risposta semplice, per quanto ne so io, e che la cosa andrebbe studiata a fondo. La stessa equazione di Bernoulli, che consente di calcolare la pressione di un fluido in transito dentro una superficie, può fornire solo un dato qualitativo perché l'aria è comprimibile, e non priva di viscosità.
Questa "spiegazione" della fisica del paracadute mi fa venire in mente in mini quiz:
Invece di avere un paracadute siete appesi ad una enorme bolla di sapone.
La bolla e voi con lei , state cadendo ad una certa velocità con la prospettiva di sfracellarvi al suolo.
Però avete a disposizione una valvolina che vi permette di sgonfiare a vostro piacimento l'enorme bolla.
Riuscireste a salvarvi? e come?
quiz quiz quiz
Caro Leandro, grazie per questa interessante appendice che proponi. Spero che i lettori colgano l'invito e propongano soluzioni utili per non spiaccicarsi al suolo, usando accortamente le risorse ( bolla con valvolina) che sono disponibili nel quiz.
Mi viene in mente cosa è successo alla sonda Schiaparelli, su Marte , giusto un paio di anni fa.
Se l'ESA frequentasse di più l'infinito Teatro del Cosmo, si eviterebbe di sprecare denaro pubblico.
Per dare spazio a tutti i punti di vista, sulla vicenda Schiaparelli, mi sembra corretto segnalarvi questo link:
http://www.infinitoteatrodelcosmo.it/2016/10/22/un-nuovo-cratere-su-marte/
Thanks Maurizio, in effetti anche considerando una semplice calotta sferica rigida che si muove in orizzontale calcolare l'onda di pressione non sembra una cosa semplice.
Conobbi un pilota che si prese una medaglia durante la seconda guerra mondiale perché, essendo stato colpito, dopo aver ordinato a tutto il suo equipaggio di lanciarsi con il paracadute, è riuscito a salvare l'aereo con un atterraggio di fortuna dalle parti del Garda. Mi confessò che lo fece perché col... fischio che si sarebbe lanciato!
Ho volato per cinquant'anni, ho accompagnato in volo anche paracadutisti, ma mi sa che anch'io sarei stato un decorato al valor militare :-)
Caro Alberto, io ho volato solo come passeggero su aerei di linea. La strategia che avrei adottato, all'occorrenza, sarebbe stata di convincere il pilota a lanciarsi con il paracadute, in modo da poter prendere il suo posto e tentare un atterraggio di fortuna. In caso di successo, avrei potuto sperare al massimo in una decorazione al valor civile, comunque meglio di niente :-)