Categorie: Fisica classica Pianeti
Tags: rivoluzione pianeta rotazione disco proto planetario rotazione pianeta
Scritto da: Vincenzo Zappalà
Commenti:30
Perché (e come) ruotano i pianeti **
Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.
Sappiamo bene come la marea riesca a sincronizzare i periodi orbitali dei satelliti maggiori con quello di rotazione (e a volte anche con quello del pianeta). Ma… come “nasce” la rotazione attorno al proprio asse?
Le velocità di rivoluzione e rotazione (senza effetti mareali importanti) dei pianeti vanno tutte nello stesso verso; nel Sistema Solare, in particolare, è quello antiorario (se visto dal polo nord del sistema). Come mai?
N.B.: a questo punto, chi vuole divertirsi, può anche fermarsi e cercare di rispondere da solo. La soluzione la troverà di seguito.
Per capirlo dobbiamo tornare alla formazione del Sole e del suo disco proto planetario e poi conoscere le leggi di Keplero e le regole ferree del momento angolare. La spiegazione qualitativa è abbastanza semplice, ma vale la pena introdurre un paio di formulette per rendere il tutto anche quantitativo.
Per i “neofiti” ricordiamo che una stella si forma per condensazione di una nube di gas. La materia, sotto la spinta dell’autogravitazione, si aggrega sempre di più e si addensa. Si dice che la nube collassa. All’inizio è enormemente grande e, alla fine, la stessa massa si concentra in un volume molto più piccolo. In altre parole, la densità aumenta. Nell’Universo niente può in realtà stare fermo e quindi anche la nube che sta collassando ha una sua propria rotazione iniziale, impartita dagli scontri avuti con altre nubi o da addensamenti locali o da mille altre possibili ragioni. Tuttavia, una rotazione anche lentissima, a mano a mano che la massa si concentra e diminuisce il proprio volume, è costretta a velocizzare la rotazione (fanno eccezione le stelle massicce, che continuano a ruotare lentamente, apparentemente in barba alle più elementarri leggi della fisica: NEWS!! il mistero è stato svelato dal sempre più mitico ALMA).
Questo fatto deriva dalla conservazione del momento angolare della nube. Esso non può cambiare e se diminuisce il raggio della sfera deve aumentare la velocità di rotazione. Ricordate la pattinatrice sul ghiaccio? Come fa a girare più veloce? Stringe le braccia verso il corpo, diminuendo la sua “larghezza”. La conservazione del momento angolare fa il resto e magari regala anche una medaglia d’oro. Un caso classico e macroscopico è quello delle stelle di neutroni.
Tornando a stelle “normali”, come il Sole, ne consegue che tutta la materia che presto finirà per formare la stella e il disco di gas e polvere che la circonda ha una velocità di rivoluzione diretta nello stesso verso. In realtà, la stella è molto magnanima (anche perché non può superare certi valori) e “regala” parte del suo momento angolare al disco che la circonda. Questo è più esteso della stella vera e propria e quindi vi è un’equa ripartizione del momento angolare di rotazione della stella e di quello di rivoluzione delle particelle che formano il disco. Nel caso del Sole questa direzione è quella antioraria, ma questo è solo un caso, legato all’origine stessa della nostra stella e, forse, anche alla rotazione dell’intera galassia.
Cosa abbiamo dimostrato finora? Solo che la rotazione del Sole intorno al proprio asse e la rivoluzione delle particelle di gas e polvere che formano il disco proto planetario hanno una velocità diretta nello stesso verso. A questo punto dobbiamo introdurre le leggi di Keplero. Esse ci dicono che più un oggetto è lontano dal Sole e tanto più è bassa la sua velocità di rivoluzione. In particolare, si trova che la velocità tangenziale di una particella (consideriamo le orbite circolari, dato che così erano all’atto della formazione) è data da:
v = √k/d
Dove v è la velocità, d la distanza dal Sole e k una costante che ci interessa poco, in quanto noi vogliamo fare un confronto tra le velocità di oggetti vicini e di oggetti lontani. Il più vicino abbia, ad esempio, velocità v1 (e distanza d1) e il più lontano v2 (e distanza d2). Dato che k è una costante per tutti, vale la relazione:
√v2 d2 = √v1 d1
e, infine:
v2 = √v1(d1/d2)
A parte le semplici formule, il “succo” è che, qualitativamente, più si è lontani e più piano ci si muove.
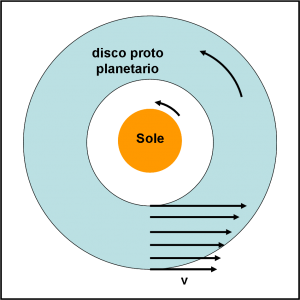
Questa semplice conclusione, ottenuta dalle altrettanto semplici leggi di Keplero, ci permette di rappresentare quanto descritto nella Fig. 1, dove le varie frecce indicano le velocità di rivoluzione in funzione della distanza dal Sole. Stiamo bene attenti a non pensare che il disco sia qualcosa che si muove solidalmente intorno al Sole. Esso è composto da singole particelle che seguono ciascuna il moto imposto dalle leggi di Keplero. Ognuna è come se fosse un singolo corpo celeste, indipendente dagli altri (escludendo, per adesso, la mutua gravità).
A questo punto, costruiamo un pianeta, ad esempio la Terra. Come possiamo fare? L’unico modo è addensare particelle che abbiano orbite abbastanza vicine tra loro. All’inizio ci sono urti reciproci, che fanno “danzare” da una parte all’altra il corpo che inizia a crescere. Poi, sempre più prepotentemente, comincia a comandare la gravità del nocciolo che si è costruito e che possiamo chiamare proto pianeta. Esso è in grado di catturare altri corpi più piccoli che stanno su orbite anche abbastanza lontane da lui. Sempre più velocemente “pulisce” una fascia di orbite che lo circonda.
Questo meccanismo è quello che è servito a trasformare Plutone da pianeta a pianeta nano. Il piccolo e lontano corpo celeste NON è riuscito a “pulire” la zona intorno alla sua orbita. Un oggetto non abbastanza efficiente, a causa della sua massa limitata e della particolare posizione occupata.
Torniamo alla Terra. Essa, ormai, è in fase di crescita sempre più rapida e su di lei piovono oggetti provenienti sia dall’esterno che dall’interno.
Siamo pronti a commettere un errore fondamentale: considerare solo le collisioni e o -se volete- la quantità di moto che viene trasferita al proto pianeta.
Questo errore viene raffigurato nella Fig. 2. Le particelle che picchiamo sul pianeta in costruzione sono di due tipi: quelle esterne che hanno velocità minore del pianeta e quelle interne che hanno velocità maggiori. Fin qui nessun errore. Lo abbiamo appena stabilito grazie alle leggi di Keplero (QUI spiegate in modo semplicissimo).
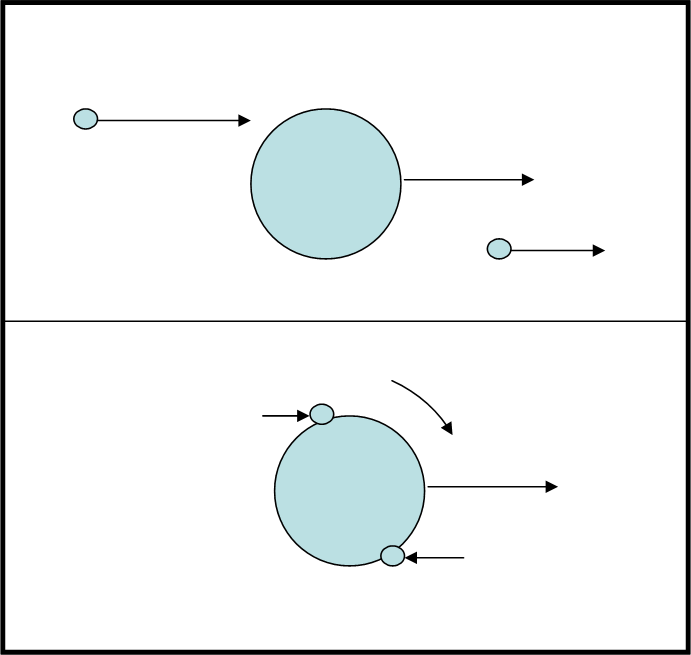
Se considerassimo solo questi urti, avremmo che la proto-Terra riceve delle “botte” da dietro da parte delle particelle più veloci e delle “botte” dal davanti da parte delle particelle più lente (quella che conta è la differenza di velocità tra particelle e proto-Terra). La quantità di moto che acquista il pianeta (la quantità di moto delle particelle è uguale a mv, dome m e v sono massa e velocità delle particelle) sembrerebbe far ruotare il pianeta in senso orario, ossia in modo contrario alla rivoluzione. Nel bordo esterno lo spingiamo verso sinistra e nel bordo interno verso destra, ossia lo facciamo girare in senso orario.
Lavorando in questo modo troveremmo proprio il contrario di quello che succede in realtà. Dobbiamo avere dimenticato qualcosa! Questo qualcosa è la forza di gravità della futura Terra.
Studiamo da vicino la configurazione generale, molto più corretta. Il nocciolo originario occupa un’orbita ben definita e quindi ha una velocità di rivoluzione altrettanto definita. Scriviamo dei numeri veri in modo da rendere più “concreta” la situazione.
A 150 milioni di chilometri dal Sole, la velocità orbitale è di circa 107 855 km/ora. Una particella che, invece, si trova a 0.8 milioni di chilometri più vicina al Sole viaggia a 108 144 km/ora, più velocemente… com’è ovvio che sia. Un oggetto più lontano dal Sole di 0.8 milioni di chilometri va alla velocità di 107 567 km/ora. Questi valori si possono ottenere facilmente utilizzando la formula descritta in precedenza (conoscendo k, ma potete credermi… spero…).
Tuttavia, ecco che entra in ballo la gravità della proto-Terra, ossia il nocciolo già piuttosto massiccio che domina la sua zona di spazio. Esso attira a sé sia la particella più lontana sia quella più vicina. Esse cadono sulla futura Terra con velocità diverse da quelle che occupavano nella posizione originaria. Cosa comanda questa variazione di velocità? Il momento angolare e la sua conservazione!
Quando l’oggetto più vicino al Sole viveva in modo indipendente, possedeva un certo momento angolare che non sarebbe cambiato se fosse rimasto al suo posto. Stessa cosa succedeva all’oggetto più lontano. Ma, adesso, stiamo cambiandogli l’orbita: uno viene spostato verso l’esterno e l’altro verso l’interno. Tuttavia, sappiamo ormai bene che il momento angolare dell’oggetto NON PUO’ CAMBIARE. Se cambia l’orbita (ossia la distanza dal Sole), deve cambiare la velocità di rivoluzione. La relazione è data dalla semplice formula:
dp vp= dd vd (dove p e d stanno per “prima” e “dopo”)
La massa è considerata uguale a uno.
Essa si ricava pensando che il momento angolare è uguale alla velocità angolare moltiplicata per il quadrato della distanza dal centro. Ma la velocità angolare è uguale a quella tangenziale v divisa per la distanza, da cui la formula precedente.
La conservazione del momento porta a:
vd = vp dp/dd
In parole semplici, quando il materiale si muove verso l’interno del Sistema Solare la sua velocità di rivoluzione aumenta, mentre avviene il contrario per oggetti che si muovono verso l’esterno. Tutto ciò solo e soltanto per conservare il momento angolare.
Se la particella che si trovava a 0.8 milioni di chilometri più lontana dal Sole, viene attratta dalla proto-Terra, la sua orbita si restringe (deve diventare come quella del nocciolo terrestre) e quindi giunge sul nostro futuro pianeta con una velocità orbitale maggiore di quella originaria, ossia pari a 108 141 km/ora. In modo uguale e opposto, la particella che era più vicina al Sole di 0.8 milioni di chilometri è costretta a portarsi su un’orbita più larga (quella del nocciolo terrestre, appunto) e diminuire la propria velocità di rivoluzione. Essa diventa 107 567 km/ora.
Ovviamente questi valori si ricavano facilmente dalla formula sulla conservazione del momento angolare che abbiamo indicato prima.
I corpi che giungono sulla superficie terrestre non possono più scappare e diventano parte integrante del nostro pianeta. Le loro diverse velocità di rivoluzione, e le loro posizioni periferiche, impartiscono, perciò, un “momento” al nocciolo terrestre (come succedeva per la marea) che tende a farlo ruotare intorno al proprio asse in senso antiorario, in modo analogo a quello del disco e del Sole (la particella esterna trascina più velocemente il nocciolo terrestre di quanto non faccia la sua compagna interna). Questa volta il verso è proprio quello giusto!
La Fig. 3 illustra questa situazione.
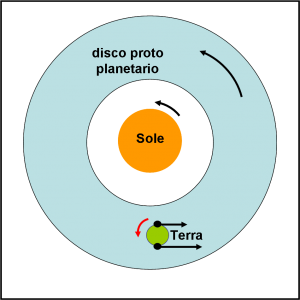
Vorrei, comunque, far presente che quanto esposto è una semplificazione di un problema sicuramente più complesso, in cui gli urti reciproci possono influenzare una visione puramente teorica. Non per niente vi sono pianeti che non seguono questa regola, in quanto la loro rotazione è stata dominata da urti catastrofici (Urano) o -magari- anche da effetti mareali (Venere). Analogo discorso vale per gli asteroidi che possono ruotare in entrambi i versi, in quanto la loro evoluzione è stata scandita dagli impatti reciproci ad alta velocità relativa.
Mi piace anche ricordare che la variazione del momento angolare e la sua conservazione aiuta non poco a creare i magnifici giochi di prestigio dei piccoli satelliti e degli anelli di Saturno (come questo, questo e questo).






30 commenti
"a questo punto, chi vuole divertirsi (uno lo conosciamo benissimo!)"
Caro Enzo, me lo presenti?
Non ho capito se vuoi la giustificazione del senso di rotazione dei pianeti (antiorario) o del fatto che ruotino tutti nello stesso senso.
Comunque, il fatto che ruotino tutti nello stesso senso credo dipenda dal senso di rotazione originario della nube che ha condotto alla formazione del sistema.
Quello che mi stuzzica è però legare il senso di rotazione (antiorario) del sistema solare al senso di rotazione galattico.
La Via Lattea ruota nello stesso senso antiorario (guarda quanto sono onesto: avrei potuto facilmente controllare ed invece mi voglio esporre alle tue pernacchie!) ?
Se si, possiamo forse pensare che la rotazione della protogalassia abbia "gettato la basi" per la rotazione del futuro sistema solare.
Se no, dobbiamo pensare che altri eventi abbiano "stabilito" le regole.
NON HO LETTO IL RESTO DELL'ARTICOLO. VA BENE ?
Come vedi mi espongo al pubblico ludibrio, caro il mio Enzone.
Ed ora mi leggo l'articolo in santa pace, porca pupazza!
A proposito di scontri catastrofici , Enzo, ti chiedo come mai la Terra non mostri anomalie di rotazione e/o rivoluzione visto che, circa 4 miliardi di anni fa, ha (avrebbe?) subito una collisione profonda con il pianeta Teia i cui effetti avrebbero poi contribuito alla formazione della Luna.
Ti chiedo inoltre se ci sono evidenze sul nostro pianeta che rimandino a quell'urto (zone a diversa composizione geologica, ad esempio) o se si tratta di una speculazione funzionale alla "creazione" della Luna, tutta da dimostrare.
Ciao e grazie.
caro Alvy,
innanzitutto la rotazione della galassia... beh, è solo un'ipotesi senza verifiche. Sappiamo poco del senso di rotazione delle altre stelle.
Poi, avrei voluto qualche calcoletto sui momenti angolari... e non solo vaghe parole su rotazione della nube proto planetaria... che va bene per il senso di rivoluzione, ma non quello di rotazione (o almeno, non è cosa diretta).
In realtà noi abbiamo un angolo di inclinazione notevole (23°) che si è stabilizzato proprio grazie alla Luna. La geologia terrestre può dire ben poco vista la sua variazione continua e il riciclaggio. Quella lunare sembra possedere le anomalie necessarie. Ma, per il momento, è più una speculazione teorica che cosa verificata, essendo l'ipotesi più favorevole e concreta.
Per i neofiti e chi se lo avesse dimenticato...
http://www.infinitoteatrodelcosmo.it/2014/11/07/alma-comincia-fare-sul-serio-le-visioni-artistiche-diventano-realta/
...dalla teoria alla realtà!!
E' emozionante riflettere sul fatto che queste "semplici formulette" siano in grado di dare una risposta scientifica all'immagine REALE di un disco proto-planetario in piena attività!
P.S.


Forza Barbara, continua così!!
Beh Enzo, visto che mi solleciti una formuletta (come se io ci tenessi particolarmente! ) ) mi permetto una piccola chiosa all'espressione da te introdotta:
) ) mi permetto una piccola chiosa all'espressione da te introdotta:
v = k/d1/2
dove v è la velocità, d la distanza dal Sole e k una costante che ci interessa poco.
Effettivamente per lo sviluppo dell'articolo la costante conta poco, ma ... può forse interessare qualcuno il semplice modo in cui si manifesta, così ripassiamo la forza centrifuga.
Si tratta semplicemente di pareggiare l'attrazione gravitazionale prodotta dalla massa centrale (Sole) alla forza centrifuga avvertita dal corpo in orbita (per semplicità, moto circolare uniforme) trovandosi, quest'ultimo, in un sistema NON inerziale:
G*M*m/R^2 = m*v^2/R
da cui:
v = (G*M/R)^0,5
Dunque k = (G*M)^0,5
Volendola ricavare numericamente:
G = 6,7*10^-11 m3/(kg*s^2)
M = 2*10^30 kg
per cui:
k = 11,6*10^9 m^1,5/s ovviamente nel caso del Sole!
grazie Daniela... e sì, hai ragione, tenendo, però, sempre in conto che la trattazione è estremamente semplificata...
caro Alvy,

sei o non sei uno dei miei migliori assistenti?! Però, però... non mi hai detto se hai ricavato prima di leggere l'articolo come funzionava il trasferimento di momento angolare... Avevi solo parlato in modo vago di rotazione del disco...
No, confesso di non essermi mai soffermato ad analizzare le modalità di trasferimento di momento angolare nel modo in cui lo hai proposto tu.
Eh beh, cosa vuoi che ti dica caro Enzo? Non vorrei che sopravvalutassi le mie capacità
No Alvy,
anzi hai dimostrato di avere molte capacità non solo scientifiche... Il nostro blog ti va a pennello! Sei diventato una pedina essenziale: tutti per uno e uno per tutti!!!
Grazie Enzo, caffè pagato alla prima occasione utile!
Caro Enzo, ho voluto giocare ancora un pò con le formule: ovviamente non ho inventato nulla, ho solo mischiato un pò le carte....generalizzando le conclusioni.
Spero di non aver fatto confusione.
Allora, definiamo con :
Ri la distanza iniziale del corpuscolo dal Sole nel nascente sistema solare.
Ri' la distanza iniziale di un secondo corpuscolo dal Sole nel nascente sistema solare.
Rf la distanza finale dei due corpuscoli dal Sole nel nascente sistema solare.
Poniamo inoltre questa condizione di simmetria:
Ri = Rf - R
Ri' = Rf + R
dove R è una distanza non meglio definita. Si vede che Ri è minore di Ri' e la distanza finale Rf raggiunta dai due corpuscoli è a metà strada tra Ri e Ri'.
Il primo corpuscolo dovrà quindi allargare la propria orbita (da Ri ad Rf), mentre il secondo dovrà restringerla (da Ri' ad Rf) in modo che entrambi possano incontrare la proto-Terra alla distanza Rf dal Sole.
Sembrerebbe che il cambiamento di orbite, data la simmetria della situazione iniziale e finale, dovrebbe fornire ai due corpuscoli la stessa velocità finale che darebbe un effetto (risultante) nullo sulla proto-Terra.
In realtà, applicando la formula generale di Enzo, si vede che:
Vf = k/(Ri^0,5) * (Ri/Rf) , ovvero:
Vf = k*(Ri^0,5)/Rf
dove Vf è la velocità finale.
Applichiamo ora la formula generale ai due nostri casi:
Vf = k*(Rf-R)^0,5/Rf
Vf' = k*(Rf+R)^0,5/Rf
Essendo (Rf-R) più piccolo di (Rf+R), si otterrà che:
Vf è più piccolo di Vf'. Il corpuscolo esterno trasferisce alla proto-Terra una quantità di moto superiore a quella trasferita dal corpuscolo più interno, proprio come si vede nella figura 3.
In conclusione, quale che sia in senso di rivoluzione del sistema nel suo complesso, la rotazione (intorno al proprio asse) dei singoli corpi (proto-pianeti, destinati a diventare pianeti veri e propri) dovrà avvenire nello stesso senso, semprechè non si verifichino urti e/o interazioni gravitazionali in grado di sconvolgere i piani.
Non vorrei aver inutilmente complicato le cose (nel qual caso ignorate quanto ho scritto)!
ovviamente sì, Alvy... Non conta il senso antiorario o orario, conta solo che la rotazione segue il verso della rivoluzione delle particelle e del disco. In qualche modo, la conservazione della sola quantità di moto sembrerebbe far girare nel verso opposto, mentre quella del momento angolare rimette le cose a posto... Puoi anche divertirti con i giochi di prestigio tra satelliti pastori e anelli. Le regole sono sempre le stesse...
Caro Enzo, è più forte di me, la curiosità mi ha spinto a chiedermi da dove venga la formula iniziale, ossia: v = k/√d
Dopo un breve ragionamento sono arrivato alla conclusione che la costante k non è altro che la radice quadrata del prodotto tra la costante di gravitazione universale G e la Massa M (del corpo maggiore, nel nostro caso il Sole).
Sono arrivato a tale conclusione (sperando sia esatta) con il seguente ragionamento.
Se un corpo si muove di moto circolare uniforme, attorno ad un corpo di massa molto più grande, il modulo della la Forza di gravità deve eguagliare quella della “fittizia” Forza centrifuga (la direzione è la stessa, passante per il centro di rotazione ed il verso è opposto).
Dato che in un moto circolare uniforme l'accelerazione vale ac = v²/r e che F=ma
la Forza centripeta (controparte della fittizia forza centrifuga) vale: Fc = m v²/r
La Forza di gravità è invece uguale a: Fg = GmM/r²
Eguagliando le due Forze, ossia ponendo Fc = Fg
mv²/r = GmM/r²
v²/r = GM/r²
v² = GM/r
v= √GM/r = √GM /√r
ponendo k =√GM e indicando la distanza dal centro di rotazione come d, invece di r, si ottiene:
v = k/√d
Dato che l'eccessivo uso di formule purtroppo produce in alcuni strane reazioni allergiche
 , per controbilanciare posto due figure che parlano da sole.....
, per controbilanciare posto due figure che parlano da sole.....
http://www.astrobin.com/full/209168/D/
http://www.astrobin.com/full/209168/E/
Infine, ho calcolato le velocità finali dei due corpi m1 e m2 indicati nelle figure.
Per trovare le velocità dopo il cambiamento di orbita di m1 e m2, sono partito dal momento angolare che si deve conservare:
L = mvr. Ponendo m=1
L = vr dato che r non è altro che la distanza dal centro di rotazione
L = v d
Affinché il momento angolare si conservi prima e dopo il cambio di orbita:
Lp = Ld (il momento angolare L si conserva)
Quindi, essendo:
vp= velocità prima
vd = velocità dopo cambio orbita
dp =distanza dal centro di rotazione (sole) prima
dd = distanza dal centro di rotazione (sole) dopo
affinché si conservi il momento angolare: vp dp = vd dd
per cui la velocità di rivoluzione dopo il cambio di orbita è uguale a: vd = vp dp/dd
Applicando questa formula, partendo dai seguenti dati:
dp = 150 106 - 0,8 106 =149,2 106 Km
dd = 150 106 Km
vp = 108 144 km/ora
Si ricava velocità di m1 dopo che l'orbita si è allargata:
vd = vp dp/dd = 108 144 149,2 106 / 150 106 = 107567 km/ora
Usando lo stesso metodo:
dp = 150 106 + 0,8 106 =150,8 106 Km
dd = 150 106 Km
vp = 107 567 km/ora
Si ricava velocità di m2 dopo che l'orbita si è ristretta:
vd = vp dp/dd = 107 567 150,8 106 / 150 106 = 108 140,69 km/ora
Spero di non aver detto qualche sciocchezza e causato qualche allergia...
Paolo
...più che allergie, caro Paolo, in me susciti una "sana invidia"...

Cara Dany, c'è poco da invidiare, sono solo un dilettante allo sbaraglio.. e poi dato che dopo aver inviato il messaggio ho letto i commenti all'articolo... ad onor del vero... Alvy aveva già perfettamente descritto come ricavare la costante K, il che mi rincuora, poiché significa che le mie elucubrazioni mentali non erano prive di fondamento.
Sono contento che non sei allergica alle formule, a mio avviso la matematica è una lingua che applicata insieme alla logica apre potenzialità pressoché illimitate.
Io mi sento un po' come un balbuziente che cerca disperatamente di associare vocali e consonanti, e sono convinto che balbuziare insieme sugli argomenti trattati possa costituire un buon esercizio collettivo per comprendere il linguaggio.
Paolo
E invece a Venere che gli sarà mai capitato???
Per me 500 milioni di anni fa gli hanno dato una bottazza e via!!!
Probabilmente un corpo di massa ben più grande delle particelle di cui si parla nell'articolo ha impattato Venere con una traiettoria tale da imprimere una rotazione oraria.
In tal caso presumo che il fenomeno trattato nell'articolo (prodotto da particelle di dimensioni ridotte) sia insufficiente per invertire il senso di rotazione prodotto da un simile mega impatto.
Ma la mia è solo un elucubrazione mentale, nulla più.
Paolo
Tranquillo Paolo plausibilmente si presume come causa scatenante l'impatto ma probabilmente dobbiamo aggiungere altri fattori come concause del singolare comportamento di Venere nel nostro sistema solare.
Appena ritrovo gli articoli che avevo letto a riguardo te li posto.
A proposito di elucubrazioni mentali, l'Energia cinetica di un corpo è uguale a:
E = ½ m v²
Quindi più aumenta la massa del corpo in movimento maggiore è la sua Energia cinetica.
Considerato che Venere ha un periodo di rotazione molto più lungo di quello terrestre (243 giorni) a mio avviso potrebbe essere lecito supporre che l'impatto sia avvenuto molto tempo fa (quindi quando il sistema solare era molto giovane) e che l'effetto descritto nell'articolo abbia rallentato la rotazione del pianeta (non era sufficiente per invertire il senso di rotazione, ma potrebbe averla rallentata).
Qui, però, per capire se una simile supposizione ha qualche fondamento occorre attendere il rientro di Enzo....
Paolo
PS: nei calcoli delle velocità finali di m1 e m2, 10 elevato a 6 è diventato 106 (purtroppo il sito non supporta apice e pedice), per cui per rendere più leggibili i risultati, li ho riscritti così:
vd = vp dp/dd = (108 144) (149,2) 10^6 / (150) 10^6 = 107567 km/ora
vd = vp dp/dd = (107 567) (150,8) 10^6 / (150) 10^6 = 108 140,69 km/ora
Paolo qui si parla di effetti mareali.....
http://www.br3nn0s.org/scienza/orb.htm
Giusto stasera pensavo di iniziare a leggere l'articolo sugli effetti mareali
 per cui essendo ignorante in materia spero di farmi un'idea più precisa su tali fenomeni e sulle risonanze orbitali
per cui essendo ignorante in materia spero di farmi un'idea più precisa su tali fenomeni e sulle risonanze orbitali 
Paolo
Per gli "ignoranti" si dice così?
 E DELLA TERRA, che possono, insieme, aver alterato il valore di rotazione citereo. I rigonfiamenti equatoriali di Venere, a causa di una serie di ritardi perdono il loro allineamento con il Sole. Di conseguenza, l'attrazione gravitazionale del Sole tende a contrastare la rotazione del pianeta aumentandone col tempo il periodo rotazionale.
E DELLA TERRA, che possono, insieme, aver alterato il valore di rotazione citereo. I rigonfiamenti equatoriali di Venere, a causa di una serie di ritardi perdono il loro allineamento con il Sole. Di conseguenza, l'attrazione gravitazionale del Sole tende a contrastare la rotazione del pianeta aumentandone col tempo il periodo rotazionale. 
Il moto di rotazione di Venere è retrogrado, in altre parole, contrario al senso di moto della Terra e della maggior parte dei pianeti. Venere compie una rotazione completa attorno al proprio asse ogni 243 giorni terrestri, valore prossimo al periodo di rivoluzione attorno al sole di 224,7 giorni. La stranezza di questa situazione E' IMPUTABILE AGLI EFFETTI MAREALI DEL SOLE
bravo Paolo come sempre...
riguardo a Venere un contributo essenziale è dato sicuramente dalla marea e dalle condizioni iniziali (che non possiamo sapere). Ad esempio, nel caso di Mercurio l'interazione di marea con il Sole ha fatto sì ogni due rivoluzioni attorno al Sole, il pianeta compia tre rotazioni attorno al proprio asse (una risonanza stabile). Per Venere non esistono risonanze particolari e la rotazione è retrograda, cioè avviene in senso opposto a quello della rivoluzione attorno al Sole. La lunga rotazione è sicuramente legata alla marea del Sole, ma è probabile che sia in parte dovuto alle condizioni iniziali con cui è nato il pianeta. Venere è un problema aperto...
Grazie Enzo!!!
Scusate sono abbastanza ignorante e ho poca praticità con le formule vorrei tanto fare una domanda a voi maestri. Ma cos'è la gravità? Perche io un'idea l'avrei.... sarà una cavolata sicuramente....grazie
Scusa Pierino, ma temo che tu stia scherzando... Penso che la gravità sia una nozione che conoscono i bambini fin dalle elementari. Sei un bambino? Se sì, puoi anche chiedere al tuo maestro. Se non sei un bambino la cosa è preoccupante... Non ti consiglio di leggere questo blog, ma un bel libro di fisica per le scuole medie... Oppure fai come Newton e aspetta che ti cada una mela in testa...
Se poi, invece la tua è una domanda più sottile che non ho compreso, ti chiedo perdono e mi aspetto una formulazione un po' più chiara... grazie...
Salve,
si riesce a trovare qualche relazione tra cambiamento della velocità angolare e modifica del campo magnetico della terra? Oppure cambiamento della velocità angolare dei pianeti vicini alla terra e modifica del campo magnetico della terra?
Thanks
caro Tarcisio,
no, non si riscontrano variazioni di questo genere (per quanto ne sappia io). La rotazione cambia solo per gli effetti mareali in modo da mantenere costante il momento angolare del sistema.