Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento

 

Avrete capito subito che il quiz, di cui questo articolo è soluzione, è stato predisposto per fare (una volta per tutte) chiarezza sul paradosso dei gemelli. Ragione per cui risolviamo il problema in vari modi, accorgendoci che, alla fine, si usa sempre lo stesso concetto, quello del cambiamento di sistema di riferimento inerziale.

Non aspettatevi un riassunto o una rielaborazione di quanto già si può trovare negli approfondimenti di questo Circolo. Per dimostrare certi concetti rimanderò costantemente a loro. Solo così, si può realmente inserire il problema particolare in un contesto più generale e completo. Inoltre, una bella rinfrescata non fa mai male.

Se leggete in giro per la rete, troverete decine e decine di spiegazioni, spesso in contrapposizione. Alcune sono decisamente errate, altre affrontano il paradosso sotto condizioni diverse. In qualche caso si preferisce non chiamarlo nemmeno paradosso, anche se è nato proprio per mettere in difficoltà la teoria della relatività. Non potrò, perciò, essere esaustivo, ma mi limiterò a presentarvi TRE METODI (che sono poi quattro o anche cinque) che sembrano molto diversi, ma che in fondo esprimono sempre lo stesso concetto: la Relatività Ristretta si applica solo e soltanto a due sistemi inerziali in movimento reciproco o, quantomeno, solo in questa situazione si ha una perfetta simmetria. Le cose non funzionano più se i sistemi diventano tre… mi spiegherò meglio.

Innanzitutto, chiariamo subito un fatto: il paradosso si risolve immediatamente (anche se non è poi così ovvio per tutti), giudicando il problema come un qualcosa legato alla Relatività Generale. In realtà, non esiste astronave che possa partire, arrivare in un certo luogo, invertire marcia e ritornare al punto di partenza senza accelerare e decelerare. Questa semplice constatazione esclude una trattazione mediante la sola RR e quindi giudica il paradosso non realistico, in quanto patrimonio della RG, dove il risultato (il gemello viaggiatore risulta più giovane del gemello che sta fermo) è del tutto ammissibile dato che solo uno dei due risente di un campo accelerato, con le conseguenze del caso.

In realtà, attraverso integrazioni si potrebbe anche utilizzare la RR come un approccio valido istante per istante e arrivare comunque alla soluzione simile a quella della RG. Ricordiamo, infatti, che la RG si costruisce proprio approssimandola punto a punto con la RR,  ma non complichiamoci la faccenda che è giù abbastanza controversa di per sé.

Consideriamo, allora il nostro quiz e vediamo di rispondere, ragionando nei modi più semplici e intuitivi. Ovviamente, per ogni metodo che useremo è fondamentale conoscere le basi della RR e, ancora meglio, saper disegnare nel diagramma di Minkowski.

Il metodo più rapido si ricollega al quiz della volta precedente, ossia a quello che doveva portare alla comprensione del concetto di tempo proprio. Ricordiamo ancora che per tempo proprio (uguale in ogni sistema di riferimento) si intende il tempo segnato da un solo orologio che misuri il tempo in un sistema che non si muova spazialmente. Vi ricorderete che abbiamo risolto il quiz della volta scorsa proprio imponendo l’uguaglianza a zero della posizione iniziale e finale. Questa asserzione ci riporta alla relatività classica di Galileo (di cui abbiamo parlato QUI alle vedi figure 4 e 5 e QUI in modo ultrasemplificato adatto anche ai più piccoli): non è possibile dimostrare che si sia in moto o fermi in un sistema inerziale. In altre parole, non esiste un sistema di riferimento assoluto e ogni sistema può considerarsi immobile. Quante volte abbiamo usato questo concetto parlando di Coriolis? Tante, forse troppe…

Chi sta sulla Terra vive chiaramente un suo tempo proprio e può usare un solo orologio per misurare il tempo. La stella Alpha Centauri (AC) appartiene allo stesso sistema di riferimento (la distanza rimane invariata) e quindi il suo orologio è perfettamente sincronizzato con quello della Terra. Durante tutto il viaggio dell’astronave del gemello astronauta, il sistema Terra-AC si sente immobile e il tempo passato tra l’evento “partenza dell’astronauta” e l’evento “ritorno dell’astronauta”, è un tempo proprio del suo sistema. Lo si può misurare tranquillamente con un solo orologio e non ci vuole molto a calcolare quanto sarà lungo: la stella dista 4 anni luce. Viaggiando a 0.8c, ci si impiega 5 anni. Il ritorno è perfettamente analogo, per cui non ci sono problemi a prevedere un tempo proprio di 10 anni.

Prima di proseguire, immaginiamo che i gemelli conoscano i rudimenti della RR e quindi sappiano che il Sig. Einstein ha dimostrato che l’orologio di chi viene considerato in moto appaia a chi sta fermo rallentare sempre di più al crescere della velocità. Se l’astronave andasse alla velocità della luce, l’orologio verrebbe addirittura visto fermo. Lo hanno imparato utilizzando l’orologio di luce e lo hanno anche descritto graficamente, utilizzando il diagramma di Minkowski.

Tuttavia, sanno benissimo che la faccenda è perfettamente simmetrica. Il gemello sull’astronave si sente immobile e per lui è la Terra (o la stazione spaziale) che si muove con una velocità uguale e contraria. Sarà lui, adesso, che giudica l’orologio del sistema Terra andare più piano del suo. Il succo di tutto, come abbiamo spiegato a lungo nell’approfondimento sulle basi della RR, è la relatività della simultaneità: ciò che è simultaneo per un sistema non lo è per l’altro. Il diagramma di Minkowski ne dà una dimostrazione immediata che potete trovare nell’approfondimento relativo e, in particolare, descrivendo le figure 33 e 34. Cosa vuol dire tutto ciò?

Se l’astronave continuasse a viaggiare nello spazio senza tornare indietro, non esisterebbe nessun paradosso: ognuno dei due sistemi vedrebbe l’orologio dell’altro rallentare e penserebbe che è il gemello in movimento che si mantiene decisamente più giovane (il suo orologio non solo meccanico, ma anche biologico, sembra viaggiare più lentamente). Se volessimo veramente confrontare i tempi dei due sistemi dovremmo usare i relativi tempi propri. Questi sono uguali per tutti i sistemi, per cui, in realtà, l’età sarebbe la stessa. Attenzione, però, che i sistemi sono considerati alla Einstein, ossia muniti di infiniti orologi e righelli e non c'è bisogno di inviare segnali.

Torniamo, allora al nostro quiz. Il gemello fermo sulla piattaforma (solidale con la Terra) risponde a una domanda molto ambigua: “Quanto tempo impiegherà il mio gemello ad andare su Alpha Centauri?”. Per poterlo veramente confrontare con il suo  tempo proprio non può eseguire il calcoletto basato su “data una velocità e una distanza spaziale posso trovare il tempo impiegato dal mio gemello per arrivare su Alpha Centauri”. Vi è un grave errore di fondo (e questo ci riporta al quiz precedente): quello che sta calcolando non è un tempo proprio, dato che il punto di partenza e il punto di arrivo per lui hanno una certa distanza (4 anni luce). Ne segue che il tempo trovato NON può essere il tempo proprio dell’astronauta, per il quale la posizione spaziale non cambia: lui deve solo aspettare che Alpha Centauri arrivi da lui. Il tempo necessario sarà il vero tempo proprio dell’astronauta.

Ripeto ancora il concetto: una cosa è il tempo proprio del gemello terrestre che intercorre tra un evento (partenza) e un altro (arrivo), entrambi appartenenti al suo sistema di riferimento; un’altra cosa è il calcolo che lui potrebbe fare del tempo di viaggio dell’astronave che appartiene a un altro sistema, in movimento. Facendo questo calcolo misura un tempo improprio, dato che il tempo proprio può essere misurato solo da chi si sente fermo e usa un solo orologio.

Sappiamo benissimo come calcolare questo tempo proprio (ricordiamo l’orologio di luce). Basta dividere il tempo improprio calcolato sulla Terra (immaginata ferma) per il fattore di Lorentz γ.

Immaginiamo di fare il calcolo per la prima metà del viaggio, durante il quale i due sistemi sono veramente inerziali. Essendo la velocità di 0.8c, si deriva che

1/γ = √(1 – (v/c)²) = √(1 – 0.8²) = √(1 – 0.64) = √0.36 = 0.6

Il tempo improprio t_IT misurato da Terra è di 5 anni, da cui segue che il tempo proprio dell’astronauta t_PA risulta:

t_PA = 0.6 t_IT = 0.6·5 = 3 anni

Fino a qui non esiste nessun risultato paradossale. L’astronauta misurerebbe una cosa simile calcolando il tempo proprio del sistema Terra, dato che sappiamo che spostandosi nello spazio del sistema Terra (dalla Terra ad AC) il tempo che vede passare nel sistema Terra è un tempo improprio.

Tuttavia, il problema sembrerebbe banalissimo (e lo è) per entrambi i sistemi. Il ritorno non dovrebbe cambiare le cose e quando l’astronauta ritornerà a casa tutto si sistemerà in qualche modo.

E invece, il risultato è ben diverso. Basta pensare che il ritorno dell’astronave alla Terra comporta un ulteriore tempo di 5 anni per il sistema Terra, per ovvi motivi di simmetria. Tempo improprio era e tempo improprio rimane. L’orologio non può sbagliare e segna 10 anni. Il risultato è corretto, in quanto tra l’evento partenza e l’evento ritorno è stato usato un solo orologio. Ma non può sbagliare nemmeno il tempo proprio dell’astronauta: se era 3 anni all’andata DEVE essere per simmetria 3 anni anche al ritorno. Se fosse così la RR sembrerebbe andare a farsi friggere… Purtroppo sembra proprio così, in quanto il gemello sulla Terra nell’evento ritorno ha 30 + 10 = 40 anni e l’astronauta 30 + 6 = 36.

Tutta da buttare la RR? Nemmeno per sogno, dato che sono stai usati TRE sistemi inerziali. Quello della terra-AC, quello dell’astronauta che raggiunge AC e quello dell'astronauta che da AC torna sulla Terra, invertendo il verso del moto. In pratica cosa succede? Cercherò di esprimerlo con parole semplici e senza calcoli. Dobbiamo tornare alle figure 33 e 34 che abbiamo già studiato.

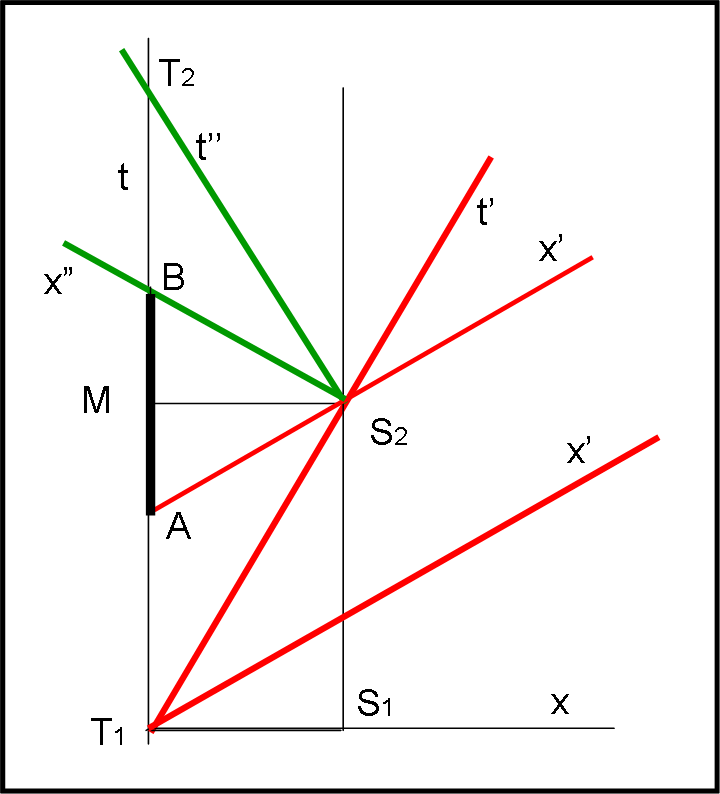
Quando l’astronauta arriva su Alpha Centauri  l’asse spazio x’ del suo sistema dimostra che è valida la RR, dato che lui incontra l’asse delle t (verticale) del sistema Terra ben prima dei 5 anni (vedi figura successiva, dove al posto di AC abbiamo inserito S). Vedrebbe quindi più giovane il gemello terrestre. Quando però riparte, dopo avere invertito la rotta, il suo nuovo asse x” incontra l’asse t molto più in alto di prima. In poche parole, in un tempo praticamente zero per l’astronauta, sulla Terra è passato un tempo estremamente lungo. Invertendo la rotta, è come se fosse subentrato un secondo astronauta che parte da AC a un tempo decisamente più grande rispetto a quello corrispondente all’arrivo del primo astronauta. In parole molto semplici il tempo passato sulla Terra tra A e B (non certo trascurabile) si annulla con l’inversione della rotta per l’astronauta.

 

Tuttavia, non voglio battere troppo su questo procedimento (il più classico). Basta dire che devo paragonare il tempo trascorso tra due eventi sulla Terra e sull’astronave. Non vi è dubbio che devo confrontare i 10 anni con i 6 calcolati usando la RR sia all’andata che al ritorno . Ricordiamo ancora che il tempo proprio si misura con un solo orologio, mentre il tempo improprio ha bisogno di almeno due orologi e tutto si riduce a un problema di simultaneità relativa.

Il quiz sarebbe risolto, dimostrando nel contempo la motivazione del cosiddetto paradosso. Esso non esiste, dato che la soluzione si trova, introducendo un terzo sistema di riferimento o -se preferite- un cambiamento repentino di sistema e quindi un salto repentino dell’asse di simultaneità da x’ a x”, come illustra in modo qualitativo la figura  precedente.

N.B.: PapalScherzone si è irritato un pochino e mi ha ordinato di essere un po' più chiaro... Come dirgli di no? E, allora, in appendice,

trovate una spiegazione più dettagliata... E che sia contento e non mi chieda di più!

Si può, però, sintetizzare e dimostrare  l’intera faccenda (oltre che risolvere il paradosso), considerando i due triangoli uguali T₁S₂M e T₂S₂M. Essi descrivono l’invariante relativistico, da cui si dimostra che il lato T₁S₂ è sempre più corto di T₁M e analogamente per quello di sopra. In poche parole il percorso T₁S₂T₂ si svolge in un tempo sempre minore di T₁T₂. Per comprendere meglio il risultato basta riflettere sulle Fig. 45 e 46 dell’approfondimento su Minkowski. Tra parentesi, nello stesso modo si può trattare anche un moto accelerato, integrando su una linea curva, che evidenzi accelerazioni continue e regolari.

Con l’invariante e la sua definizione si risolve il nostro problemino, così come fatto da Oreste QUI, per determinare il tempo proprio, che è proprio l’invariante.

Ricordiamo, adesso, un altro metodo che, come già ho fatto presente in altre discussioni, non amo in modo particolare. O, almeno, non lo amo quando viene utilizzato al posto della RR. Ossia, utilizzare realmente un astronauta e un osservatore terrestre (e non i loro sistemi in generale), tali da potere osservare ciascuno l’orologio dell’altro (o accorgimenti del genere). In pratica, si deve tener conto del tempo necessario ai segnali luminosi per partire e per arrivare. Il metodo tiene conto, perciò, anche del tempo che la luce impiega a raggiungere effettivamente i due gemelli. In qualche modo si mischia la vera RR con un suo effetto, ossia l’effetto doppler relativistico, che abbiamo pubblicato QUI. Come ben descritto da Umberto, esso permette la soluzione, ma invito ad andare direttamente nell’approfondimento di Minkowski, dove il tutto è descritto anche cambiando sistema di riferimento (capitolo: Manteniamo il contatto visivo e il paradosso si dissolve, da Fig. 24 a 29).

Non possiamo dimenticare che per tracciare le linee del diagramma di Minkowski si deve usare la dilatazione dei tempi e quindi la RR entra di prepotenza nella trattazione, così come succede per il calcolo dell’effetto doppler relativistico. Tuttavia, non voglio continuare a discutere la validità “profonda” di questo metodo che potete trovare in vari siti del web. Addirittura, si può anche ricavare la RR partendo da questo effetto e cento altre variazioni sul tema.

Io penso, comunque, che quanto scritto nei vari approfondimenti sia più che sufficiente per avvicinarsi adeguatamente alla RR. Non chiedetemi, perciò, di entrare nei dettagli di altri metodi che non mi sembrano né più corretti e nemmeno più semplici. Direi che per capire l’essenza della RR e risolvere il paradosso dei gemelli ne abbiamo a sufficienza.

A questo punto, direi di aver non solo risolto il quiz, ma anche aver girato e rigirato il paradosso dei gemelli in modo sufficientemente completo e intuitivo.

Permettetemi, però, di proporvi (nel prossimo articolo) una specie di favola, che ricorda tanto quella del nostro amico Muo (QUI), anzi la potremmo chiamare la “doppia” favola di Muo1 e di suo fratello gemello Muo2. In fondo, potrebbe essere il modo migliore e più intuitivo per capire e risolvere il paradosso, così come è stato banale comprendere la favola di Muo. Nello stesso articolo vedremo anche una versione tipica del nostro amico Maurizio, alias (quando vuole) Oreste Pautasso.

Appendice:

Facciamo riferimento alla figura precedente...

Gli orologi dei due gemelli sono sincronizzati alla partenza. Cosa ci diranno alla fine del viaggio?

Per G (gemello terrestre) l’evento M è simultaneo a S₂.

Per G’ l’evento A e simultaneo a S₂.

Per G’ l’evento B è simultaneo a S₂.

Ossia A è simultaneo a B…  per G’ il tempo AB non esiste.

Potrebbe bastare così, ma si può andare nei dettagli

Ci mettiamo nei panni di G

t_T1T2 = t_T1M + t_MT2

Come valuta G il tempo misurato da G’?

t’_T1S2T2 = t’_T1S2 + t’_S2T2.

Per G, che è istruito, t’ _{T1S2 e}  t’ _S2T2 sono tempi propri (misurati da chi non si muove) per cui può scrivere (sapendo che M e S₂ sono simultanei nel suo sistema):

t’ _T1S2T2 = t_T1M /γ + t_MT2/γ

Secondo G il tempo che misura G’ è minore del suo:

t’ _T1S2T2 = (t_T1M + t _MT2)/γ

t’ _T1S2T2 < (t_T1M + t _MT2) = t_T1T2

t’ _T1S2T2 <  t_T1T2

Quanto riportato è il ragionamento di G, che sa calcolare il tempo passato da G’.

Cosa pensa G’ del tempo passato da G:

t_T1T2 = t_T1A + t_BT2

dato che il tempo AB non esiste

Adesso può calcolare il tempo del suo orologio

t’_T1S2T2 = t’_T1S2 + t’_S2T2

Ma sa anche che S₂ è simultaneo  ad A e, contemporaneamente, a B e quindi può calcolare, sapendo che t’_T1S2 e t’_S2T2 sono tempi propri, che:

t’_T1S2T2= (t_T1A + t_BT2)/γ

t’ _T1S2T2 < (t_T1A  + t _BT2) = t_T1T2

t’ _T1S2T2 <  t_T1T2

Per entrambi i sistemi il tempo passato dal gemello viaggiatore è minore di quello del terrestre

CONTENTO SCHERZY ? (Ma con tanti simpatici papallicoli proprio lui dovevamo ospitare qui da noi?   )

 

QUI tutti (o quasi) gli articoli riguardanti il paradosso dei gemelli