Categorie: Relatività
Tags: introduzione mollusco di Einstein principio equivalenza relatività generale sistemi inerziali spaziotempo curvo verso la RG
Scritto da: Vincenzo Zappalà
Commenti:15
Un bambino e le sue semplici domande: Einstein e la Relatività Generale **
Questo articolo, che arriva per ultimo, avrebbe dovuto essere il primo, in quanto “cerca” di introdurre la Relatività Generale da un punto di vista abbastanza particolare, che, però, assomiglia sicuramente al carattere fanciullesco di Einstein. Un metodo saltellante e poco logico? Beh… anche in questo senso ho cercato di avvicinarmi alla formulazione di Albert, che, in fondo, non sapeva nemmeno lui cosa cercare e come cercarla. Aveva solo grandi dubbi e qualche domanda molto semplice, semplice come l’intero Universo. Un uomo vero, un figlio del Cosmo, forse il solo che parlando lo stesso linguaggio, poteva superare un confine apparentemente insuperabile.
Dopo aver costruito una splendida struttura con i LEGO o con il “vecchio” MECCANO, un bambino è normalmente insoddisfatto. Superato il primo, effimero, momento di trionfo e di gioia, subentra immediatamente la domanda: “E adesso…?”. La costruzione è bella, ma è limitata. Il bimbo vorrebbe di più e subito. Non gli resta che chiedere ai genitori la scatola successiva e la conclusione è la solita frase: “Non sei mai contento!”.
Bene, Einstein si trovava sicuramente nello stesso stato d’animo dopo aver descritto la Relatività Ristretta e le sue sbalorditive applicazioni alla dinamica. In fondo non era stato così difficile… Newton era stato relegato a genio, sicuramente immenso, ma costretto a muoversi all’interno delle rigide pareti di un mondo limitato, dove la luce aveva una velocità che poteva essere considerata infinita. Di fronte ai risultati dell’elettromagnetismo Einstein non poteva che farsi una domanda quasi banale: “Perché le cose non funzionano?”.
La sua mente quasi infantile non poteva che darsi una risposta altrettanto semplice: “Perché la luce ha una velocità limitata”. In questo modo era “facile” dimostrare che nei sistemi inerziali i fenomeni fisici rimangono gli stessi. Una risposta semplice a una domanda semplice. Una risposta che può essere tradotta in: “Lo spazio e il tempo devono essere strettamente collegati tra loro”. Pensiamoci bene… Lo spaziotempo non nasce da un teoria piena di formule e di teoremi matematici, ma da una semplice domanda a cui Einstein ha risposto nel modo più “ingenuo”. E’ stato poi facile applicare alla sua idea di base la trasformazione di Lorentz. Una formula matematica che diventava improvvisamente l’essenza del Cosmo. Albert ha dato vita a una “parola” di per sé fredda e rigida.
A questo punto, avendo trovato la chiave di lettura dell’Universo, attraverso un linguaggio infantile, non gli è stato difficile arrivare all’uguaglianza tra massa ed energia e alla più famosa formula della Scienza (E=mc2 che abbiamo spiegato QUI). L’applicazione al microcosmo, l’unico che sembrava obbedire alla sua rivoluzione epocale, portava con sé spiegazioni quasi banali sui decadimenti radioattivi e sulle tante proprietà della materia all’interno delle stelle e non solo. Perfino i muoni sembravano corrergli incontro per ringraziarlo di avere fatto luce sul loro mondo misterioso.
Sì, tutto grande e geniale, ma… “E adesso…?”. In fondo aveva “solo” dimostrato che tutti fenomeni della fisica devono essere uguali nei sistemi inerziali, che spazio e tempo non sono separati, che massa ed energia sono praticamente la stessa cosa. No, non poteva bastargli… ma non sapeva nemmeno che domande farsi esattamente. Sicuramente avrebbe voluto estendere la sua relatività anche ai sistemi non inerziali.
Troppe cose sembravano vaghe e artificiose. L’importante, però, era restare bambino senza aver paura di chiedere qualcosa di più basandosi solo su formulazioni della massima semplicità. L’uovo di Colombo era sempre pronto a colpire. Ecco, forse, la dote più grande di Einstein: non aver mai avuto paura di dubitare anche delle cose più assodate e, nello stesso tempo, non aver mai avuto paura di farsi domande apparentemente banali e di rispondere in modo apparentemente ingenuo.
La grandezza di uno scienziato, capace di trasformare la visione di un Universo non ancora osservato, sta proprio nell’umiltà delle proprie domande e risposte. Prima delle formule complicate ci vogliono le idee e queste nascono, a volte, più nelle menti infantili che in quelle troppo sofisticate e artefatte.
Prima di iniziare il travagliato e fanciullesco tragitto che lo ha portato alla teoria più generale mai costruita, ricordiamo che Einstein è passato attraverso idee ed esperimenti mentali spesso ingenui, abbozzati o addirittura errati, con tutta la passione e semplicità di cui era capace. Questo gli ha permesso di costruire una vera opera d’arte, un qualcosa di estremamente semplice nella sua struttura, capace di risolvere, però, problemi che non si erano ancora minimamente affacciati alla conoscenza umana. Ogni suo tentativo lo ha aiutato a preparare la mente ad aprirsi alle idee risolutive che si accendevano come lampadine. Facciamo un esempio molto indicativo.
L’idea di un sistema di riferimento assoluto e la fumosità di tutte quelle forze apparenti che bisognava introdurre per spiegare lo stesso fenomeno in sistemi non inerziali. La sua mente cominciò a formulare domande semplici, quelle che corrispondevano meglio al linguaggio dell’Universo. Un problema lo assillava: la RR aveva dimostrato che non esisteva un sistema di riferimento assoluto, ma solo sistemi in moto relativo. Perché mai la stessa cosa non poteva valere per i moti accelerati? Una semplificazione ovvia per chi pensa in modo semplice. Un moto accelerato comporta fenomeni diversi per un osservatore in stato di quiete. Perché mai moti inerziali e moti accelerati devono essere trattati diversamente? E cosa significa stato di quiete?
E fece un esempio banalissimo...
Prendiamo due pianeti liquidi posti lontano e isolati nello spazio (Fig. 1): uno ha la forma schiacciata come quello della Terra, l’altro è una sfera perfetta.
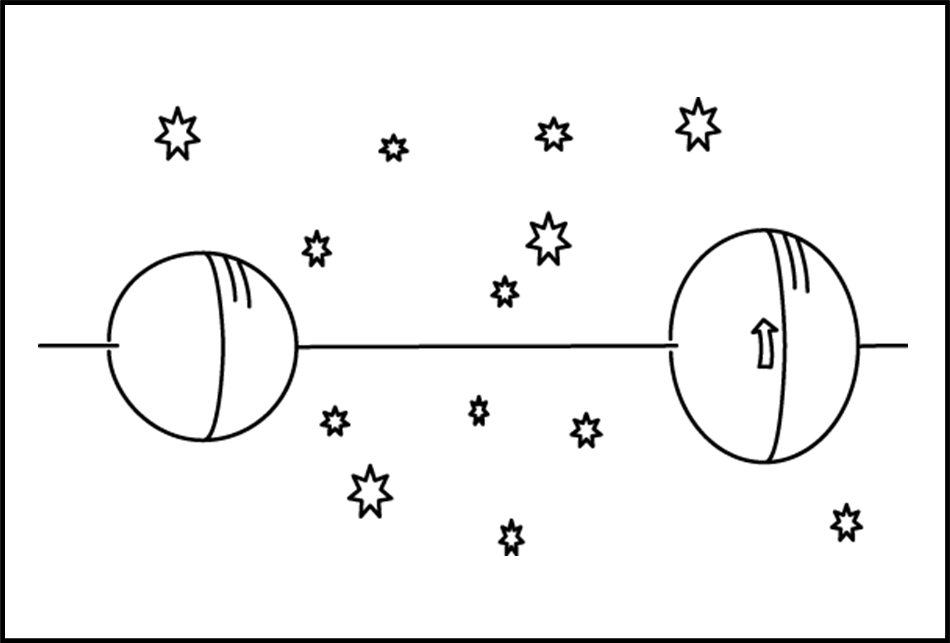
Consideriamo per loro un solo asse di rotazione. Attenzione, però, parliamo di rotazione relativa. Ossia chi sta sul pianeta sferico vede girare l’altro e viceversa. Quello allungato gira sicuramente e lo dimostra la sua forma, ma se ci portiamo su di lui anche quello sferico appare ruotare. Newton concluderebbe, però, che quello sferico non ruota rispetto a un sistema inerziale.
No, questo non piace a Einstein. Entrambi i pianeti vedono l’altro ruotare e sono entrambi isolati. Perché mai dovrebbe esistere una differenza come quella mostrata dalla sfera schiacciata? Nessuno dei due osservatori potrebbe mai dire che l’altro non ruota. In altre parole, nessuno dei due può considerarsi un osservatore privilegiato! La spiegazione di Newton “un sistema è inerziale e l’altro è soggetto alla forza centrifuga” non può essere accettabile… troppo complicata e poco armonica. Qualcos’altro deve intervenire per fare differire la forma dei due pianeti, qualcosa di OSSERVABILE.
La prima risposta che viene in mente a Einstein sono gli studi di Mach. Una soluzione non esatta, ma che lo costringe a studiare meglio la gravitazione e i suoi effetti. Nessuna paura di sbagliare se il problema viene affrontato con la massima concentrazione possibile e senza pregiudizi.
Ernst Mach pensava che le stelle fisse oppure no dominassero il moto non inerziale dei singoli oggetti. Le stelle, pur lontanissime, costringevano i corpi ad accelerare a causa della loro presenza fisica. Le stesse stelle, teoricamente, potevano subire trattamento analogo da qualsiasi altro corpo fisico. Tuttavia, la grande distanza permetteva a certi moti di apparire inerziali ed altri no. Il tutto si basava sulla distribuzione delle stelle rispetto all'oggetto in questione. I moti inerziali lo erano solo apparentemente e ciò si doveva alla configurazione del moto dell'oggetto rispetto ai corpi fisici lontani, ma presenti.
L’idea di base fu modificata da Einstein che la descrisse sotto un’ottica un po’ diversa: la distribuzione di materia nell’Universo comanda il moto di tutto ciò che esiste. Egli iniziò a convincersi che la distribuzione di massa dell’Universo era la causa della diversità tra un pianeta fluido non schiacciato e uno schiacciato. Ecco la ragione osservativa che mancava a Newton: nessuno dei due era un sistema che poteva essere considerato inerziale.
Siamo ben lontani dalle conclusioni finali, ma l’idea della massa come vera dominatrice del moto dei corpi si era già affacciata. Non solo però. Aveva già iniziato a pensare che non doveva esserci nessuna vera differenza tra sistema accelerato e sistema inerziale. Entrambi erano moti relativi.
In qualche modo, Einstein vide la via da seguire: doveva distruggere ogni separazione tra moto inerziale e moto accelerato, come appariva nella sua RR. Chi sta dentro l’ascensore che cade pensa di non essere accelerato in un campo gravitazionale, che sta fuori e non cade dice che l’uomo dentro l’ascensore sta accelerando in caduta libera. La visione dell’accelerazione diventa qualcosa di relativo.
Una serie di pensieri quasi ingenui; nessun imbarazzo a entrare in un’ottica dai risvolti poco scientifici che però lo mette di fronte a problemi nascosti; la capacità di estrarre le parti più logiche e innovative; una serie di conclusioni quasi ovvie e … la costruzione LEGO è finita! “E adesso…?”
A questo punto, va ricordata la situazione dell’astrofisica in quegli anni. Molto semplice: essa non era praticamente ancora nata e le stelle fisse non erano un pensiero da ignorante sprovveduto. Il moto dei corpi poteva essere studiato solo nel Sistema Solare e nemmeno si conosceva l’esistenza delle galassie. La loro forma a disco appiattito e l’influenza di quelle vicine avrebbe sicuramente sveltito le conclusioni preliminari, frammentarie e disordinate, di Einstein. Questo fa della teoria della RG un capolavoro ancora più grande: arrivare a spiegare gli oggetti più esotici dell’Universo (roba da tesi di laurea), quando si è ancora in prima elementare!
Un altro grande dubbio, insopportabile per Einstein, era l’effetto immediato insito nella teoria di Newton. Se, per una qualche ragione fosse spostata la massa del Sole o fosse sparito del tutto, gli effetti sulla Terra sarebbero stati immediati. Ma questo voleva dire mandare un’informazione a velocità infinita, superiore a quella della luce. E questo per Albert era impossibile. Una domanda alla portata di chiunque e una risposta che doveva essere altrettanto esauriente.
La forza a distanza non poteva, perciò, essere plausibile. L’idea che gli girò in testa fu proprio quella di una curvatura dello spaziotempo che introducesse traiettorie predefinite nelle vicinanze di una massa considerevole. Una soluzione apparentemente ovvia (o quasi) che deve la sua grandezza proprio al fatto che qualsiasi risposta era considerata da Einstein meritevole di attenzione.
Ci sarebbero moltissimi altri esempi di esercizi mentali e di dubbi. Tutti, però, sotto forma di problemi alla portata di chiunque, come formulazione. Ciò che non era alla portata di tutti era la capacità di darne una soluzione altrettanto semplice e banale. Ripetiamolo ancora: Einstein stava riuscendo a parlare con l’Universo usando il suo linguaggio, quello dell’umiltà e della semplicità assoluta.
Riassumiamo ancora una volta i punti fondamentali della RG, cercandoli di vedere sotto un aspetto quasi fanciullesco.
Non esiste effettiva differenza tra sistemi accelerati e sistemi inerziali. In particolare, un sistema inerziale non è altro che un sistema di riferimento in caduta libera che sta subendo l’accelerazione gravitazionale. Basta pensare a un ascensore a cui si è spezzata la corda o a un imbianchino che sta cadendo da un ponte. Che dire? Un esperimento (mentale) sotto gli occhi di tutti. Verrebbe da dire: “Tutto qui?”. Eppure da questa constatazione nasce il principio di equivalenza.
Lo spaziotempo non è euclideo, ma è simile a una superficie sferica o a una piastra un po’ speciale. E’ uno spazio curvo e di conseguenza i corpi immersi in esso devono seguire le traiettorie corrispondenti alla curvatura che stanno attraversando. Dopo aver descritto la RR non è difficile stabilirle: esse sono quelle che corrispondono al tempo proprio massimo. In altre parole definiscono le geodetiche.
Una visione di una semplicità sconcertante, ben superiore a quella della forza di maga Magò-Newton. Non vi è bisogno di forze, basta solo “cadere” lasciandosi trasportare dall’andamento dello spaziotempo. Lunghezze e orologi (legati strettamente dalla RR) ci verranno dietro. Chi non ha mai usato uno scivolo dalle forme più strane per tuffarsi in piscina? Basterebbe questa esperienza per capire la curvatura dello spaziotempo.
Non resta, allora, che la parte veramente difficile, quella che ha visto Einstein diventare giocoforza un matematico e attingere senza timori agli studi più avanzati sulle curvature dello spazio: determinare come la presenza di materia e/o energia possa curvare lo spaziotempo.
La Relatività Generale, in fondo, è tutta qui.
In questo contesto, simile a un gioco di bambini, risulta particolarmente suggestiva la descrizione che lo stesso Einstein dà dello spaziotempo.
Esso deve essere pensato come un “mollusco”, un’“ameba”, composto anch’esso di materia/energia. Un corpo molle che si piega, si flette, si deforma. Lo spazio è una componente materiale del Cosmo. Un’entità che si incurva e si storce. Ne segue che qualsiasi cosa viva al suo interno è costretta sia a seguirne i capricci che a modellarlo. Le masse deformano il mollusco e costringono gli oggetti a muoversi lungo le sue deformazioni. La Terra non gira intorno al Sole perché è tirata da una misteriosa forza, ma perché sta correndo dritta in uno spazio che si curva.
Cosa meglio di uno dei tanti orologi molli di Dalì può darci un esempio concreto di questo mollusco?
Non stupiamoci allora se la descrizione che daremo sarà molto saltellante e ci farà passare da un argomento a un altro senza nessuna apparente logica. In fondo, cercheremo solo di imitare il “bambino” Einstein che si annoia di un gioco e ne prende un altro per poi tornare al primo. La cosa poco “bambinesca” e straordinariamente geniale è il legame nascosto che lega i vari giochi. Un legame che può essere descritto solo con il linguaggio semplice dell’Universo.
Una volta capitane l’essenza, diventa quasi un esercizio da noiosi matematici rendere il tutto alla portata degli … uomini. Non per niente Feynman ebbe a dire che non era tanto la stupefacente teoria a sbalordire, quanto il pensare che a qualcuno fosse potuta venire in mente. Aveva ragione: solo a un uomo che viveva nell’Universo, senza ancora conoscerlo, ma che sapeva capire il suo linguaggio, poteva essere concesso di avvicinarsi alla realtà.
Tutto ciò che poteva essere verificato per pochissimi fenomeni osservabili è diventato un po’ alla volta la struttura portante dell’intero macrocosmo. Effetto lente, buchi neri, onde gravitazionali e mille altri oggetti o fenomeni non sono che l’ovvia conseguenza di una chiacchierata tra Albert e l’Universo. Un bimbo direbbe: “Che c’è di strano?”
Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.
QUI trovate l'approfondimento dedicato alla Relatività Generale







15 commenti
"La Terra non gira intorno al Sole perché è tirata da una misteriosa forza, ma perché sta correndo dritta in uno spazio che si curva."
Prendendo spunto da questa frase farei una domanda: C'è una direzione privilegiata? E se sì, come si determina?
Davvero affascinante l'immagine di questo scienziato-ingenuo-come-un-bambino che scopre la chiave di volta per spiegare l'universo e le sue regole... se ne leggono di cose su Einstein, ma questo punto di vista è davvero originale e geniale nella sua semplicità!
Quanto sarebbe facile suscitare la curiosità e l'interesse degli studenti se le lezioni tecniche fossero precedute da spiegazioni come questa?
Complimenti Prof.!
grazie Dany,
ma sai i dubbi di Albert erano talmente semplici nella sostanza che solo un vero "bambino" poteva esprimerli senza timore e senza pregiudizi... Come vorrei passare mezz'ora con lui...
Comunque, non esagerare... ho solo parlato cercando di mettermi nei suoi panni, dato che essere sempre un po' bambino mi piace tanto...
Lo so, lo so... e ti riesce anche bene!
Scusa Gimar... ma mi sembra di essere stato abbastanza chiaro nei vari articoli. La massa del Sole deforma lo spaziotempo in modo che, a seconda della velocità e della direzione, un oggetto come la Terra è obbligato a seguire percorsi obbligati che sono quelli delle geodetiche, ossie delle linee rette in uno spaziotempo curvo. Esse sono anche quelle per cui il tempo proprio è massimo. Se non ci fosse velocità la Terra piomberebbe sul Sole in caduta libera (come l'ascensore o l'imbianchino).
Grazie Enzo, ma mi rendo conto che non ho chiarito il mio dubbio. Una geodetica è una linea dello spazio-tempo con due direzioni. Se il movimento è dalla massa più piccola verso la massa più grande non è come conservare una parte dell'attrazione di Newton?
caro Gimar,
sicuramente gli effetti sono uguali a quelli della legge di Newton, ma è il motivo che è diverso. La massa più grande deforma molto di più lo spaziotempo e obbliga la più piccola a caderci dentro. Se arrivasse una stella di neutroni sarebbe il Sole ad andarle addosso o a orbitarle attorno. Tutto lo spaziotempo è modellabile a piacere a seconda della masse che si infilano dentro... Non per niente, per masse piccole la legge di Newton va ancora bene e ci permette di far viaggiare i satelliti e ad andare su Plutone. Comunque, se qualcosa ancora non ti torna, chiedi senza paura!!!
Grazie Enzo, le rotelline un po' arrugginite ce l'hanno finalmente fatta! Devo dire che mi ha aiutato, oltre alle tue risposte naturalmente, pensare ai Buchi Neri. Mi bloccava il fotone che segue la traiettoria delle geodetiche ma prosegue tranquillamente la sua strada indipendentemente dalla direzione da cui proviene. Ma poi ho pensato al B.H. che è un pozzo per le geodetiche ed anche per i fotoni.
Caro Vincenzo,
Innanzitutto complimenti per l'articolo, davvero bello.
Mi sto avvicinando da poco allo studio ed alla comprensione della relatività generale e la trovo interessantissima.
Mi é chiaro il concetto di spaziotempo quadridimensionale e di come la presenza della massa possa curvarlo e generare questi "percorsi obbligati" , delle traiettorie che masse più piccole in moto relativo rispetto ad altre più grandi devono seguire necessariamente perché é esattamente la forma dello spazio in cui si muovono.
Una domanda resta però...
Perché cadiamo?? Mi spiego meglio:
D'accordo che lo spazio in cui "precipiteremmo" é una sorta di cono diretto verso la terra, ma se un corpo tenuto sospeso da un palazzo (biglie di Galileo ad esempio) viene semplicemente lasciato, senza imprimere alcuna velocità relativa iniziale, perché cade a terra? Non potrebbe semplicemente rimanere sospeso dove già si trova senza percorrere alcuna distanza nello spazio curvo quanto si voglia? Potremmo argomentare che non ha senso dire "fermo" perché non c'è sistema di riferimento privilegiato, quindi possiamo supporre che il corpo sia già in moto relativo rispetto a qualcos'altro (sole, altri corpi celesti, etc.) ma comunque non mi é chiaro perché "inizi" un nuovo moto relativo, rispetto a chi lascia la presa ed inoltre acceleri!
Stesso discorso per buchi neri e tutto il resto. Se un oggetto è posizionato e "fermo" rispetto al buco nero, perché questi lo "risucchierebbe" al suo interno?
Chiedo scusa per la mia ignoranza e confido in una tua risposta chiarificatrice.
Grazie mille,
Davide
caro Davide,
ti rispondo nel modo più semplice possibile (per adesso). Se non ti basta andiamo più a fondo.
Lo spazio-tempo è "curvo" solo nei pressi di una certa massa. Infatti, se si potesse andare lontano da tutto ciò che ha una massa (chiamiamolo vuoto anche se è solo un qualcosa di teorico) noi resteremmo proprio fermi. Tuttavia, un qualcosa lasciato cadere all'interno dello spazio-tempo curvo è come se si trovasse sul pendio di una collina. Finché qualcosa lo trattiene sta fermo rispetto al pendio, ma se viene lasciato andare comincia a rotolare verso il centro della massa. Un satellite artificiale non cade perché ha una sua velocità tangenziale che lo fa girare senza cadere proprio come fanno certe moto nei vecchi Luna Park di una volta... ma se si rallenta ecco che si cade.
Invece di pensare a una forza che attira, devi pensare a uno spazio in cui ogni cosa è obbligata ad andare lungo una strada obbligata in discesa. Pensa al bob: all'inizio è fermo, ma poi deve cadere e lo fa solo secondo una strada ben delineata... la traiettoria spaziotemporale di Einstein..
Caro Vincenzo,
grazie mille per la tua gentilissima risposta.
Vediamo se ho capito bene (chiedo scusa in anticipo se ho frainteso qualcosa):
La cruvatura dello spaziotempo, dovuta alla presenza di grandi masse, impone alle masse più piccole nelle vicinanze, sebbene nel vuoto assoluto sarebbero ferme, di muoversi di moto uniformemente accelerato nella direzione del centro della massa più grande.
Dunque è la curvatura stessa che origina, ed é la causa del moto uniformemente accelerato.
Se é così mi sfugge ancora come possa una "pura" caratteristica geometrica dare inizio ad un moto, esattamente come fanno le altre forze che conosciamo (meccanica, magnetica, etc.) ?
Anche perché il risultato finale è esattamente lo stesso: una sfera di vetro si sfracella al suolo se lasciata cadere dal primo piano esattamente come se la lancio con forza contro un muro.
Davide
caro Davide,
anche la luce, senza massa, è obbligata a seguire la strada prefissata.
L'importante è che l'oggetto (indipendentemente dalla sua massa, ma questo lo sapeva anche Galileo) subisca la curvatura spazio temporale. Ti farei anche l'esempio del cono di luce nei pressi di una massa enorme... ma non so se migliorerei o peggiorerei il tuo dubbio. Niente cade perché è attratto da una forza, ma solo perché segue la deformazione dello spaziotempo causato da una massa di grandi dimensioni. Cerca di non pensare nelle due dimensioni come l'esempio del lenzuolo con una pietra sopra, ma portando il tutto nelle tre dimensioni: tutto ciò che entra nella zona critica è costretto a cadere nell'imbuto a 3-D che è sempre più profondo in relazione alla massa che lo causa. Dato, però, che spazio e tempo sono legati dalla RR, ne segue che è tutto lo spaziotempo (4 dimensioni) a curvarsi o -se preferisci- a deformarsi.
Tu stesso hai detto una verità epocale: Le masse deformano lo spaziotempo e lo spaziotempo impone il movimento alle masse.
Caro Vincenzo,
Grazie mille ancora per la tua gentile e illuminante risposta.
È un po' più chiaro adesso, grazie a te.
Immagino che il problema risieda nella nostra mente, abituata a ragionare dinanzi un mondo coperto da un "velo newtoniano".
Per cui ci risulta difficile accettare che un moto accelerato possa essere causato non da una forza, ma dall'intelaiatura stessa dell'esistente, che ci risulta difficile da visualizzare
Sicuramente sì, Davide...
Meno che nella MQ, dato che bene o male conosciamo una sfera a tre dimensioni, ma anche nella RR e la RG devono accettarsi le 4 dimensioni e gli effetti in 4 dimensioni della deformazione causata da una massa. Il problema è che spesso e volentieri si usano imbuti, palloncini che si gonfiano, dolci che lievitano, i quali da un lato possono schematizzare il fenomeno, ma dall'altro hanno il rischio di confondere e farci intendere tutto il palloncino come lo spazio o solo l'imbuto e giù di lì. Andrebbe subito colto un segnale fortissimo: ciò che a noi sembra in tre dimensioni, come la sfera o l'imbuto che va sempre più a fondo, sono rappresentazioni a DUE sole dimensioni. Il primo passo è convincerci che nello spazio ciò capita nelle tre dimensioni e quindi è tutta la superficie del palloncino a essere lo spazio a tre dimensioni: il raggio del palloncino che cresce è solo e soltanto una rappresentazione della quarta dimensione, ossia il tempo.
Sto scrivendo un articolo sui tensori, parola che ha sempre spaventato...Penso di essere finalmente riuscito a portare tutto a un livello estremamente divulgativo e comprensibile (pur lasciando da parte certe ricercatezze matematiche). Se lo leggerai, penso che sarà un aiuto per entrare nel mondo di Einstein e per capire quanto grande sia stata la sua rivoluzione e quanto terribilmente complessa è stata la sua rappresentazione in una sola formula dall'apparenza quasi banale. I tensori aiutano proprio a entrare nell'ottica di un corpo che subisce una deformazione nel suo moto dettata dal "vuoto" che gli sta intorno che è comandato e deformato da una massa notevole. Ricordiamoci come Einstein definiva il suo spaziotempo: un MOLLUSCO che si contare, si espnde, si piega e via dicendo. Dalì con i suoi orologi molli l'aveva capito molto bene...
Comunque, sempre pronto per qualsiasi dubbio!!
Grazie Vincenzo,
Sempre molto chiaro.
Ho qualche dimestichezza con i tensori, essendo di base universitaria un ingegnere, dunque leggero' con grande interesse il tuo nuovo articolo.
Se dovessi necessitare di chiarimenti non esitero' a chiedere!
Piacere di conversare con te.