Categorie: Fenomeni astronomici
Tags: aberrazione annua aberrazione della luce astronomia sferica coordinate celesti ellisse ellissi parallasse annua quarto sistema
Scritto da: Vincenzo Zappalà
Commenti:3
Aberrazione della luce. 3: due ellissi disegnate sulla sfera celeste **
Per una trattazione completa di questo argomento si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.
Prima di proseguire con lo studio dell’aberrazione annua e, più in generale, con i suoi effetti relativistici applicati a un astronave in volo a velocità simili a quelle della luce, cerchiamo di comprendere meglio come le ellissi apparenti si disegnino sulla sfera celeste e come si possano esprimere in termini di coordinate del quarto sistema di riferimento (QUI). Non consideratelo un discorso “noioso”…
Seguiamo il procedimento nel caso della parallasse annua e poi ci accorgeremo che basta ben poco per ottenere il risultato relativo all’aberrazione annua (anzi lo lasciamo come esercizio). Penso che questa trattazione dia anche un ulteriore aiuto per coglierne le differenze fondamentali.
Parallasse annua
Consideriamo due punti qualsiasi dell’orbita terrestre considerata circolare, T e T’. M sia una stella relativamente vicina. Disegniamo la Fig. 18 e analizziamo il triangolo MST, dove S è il Sole.
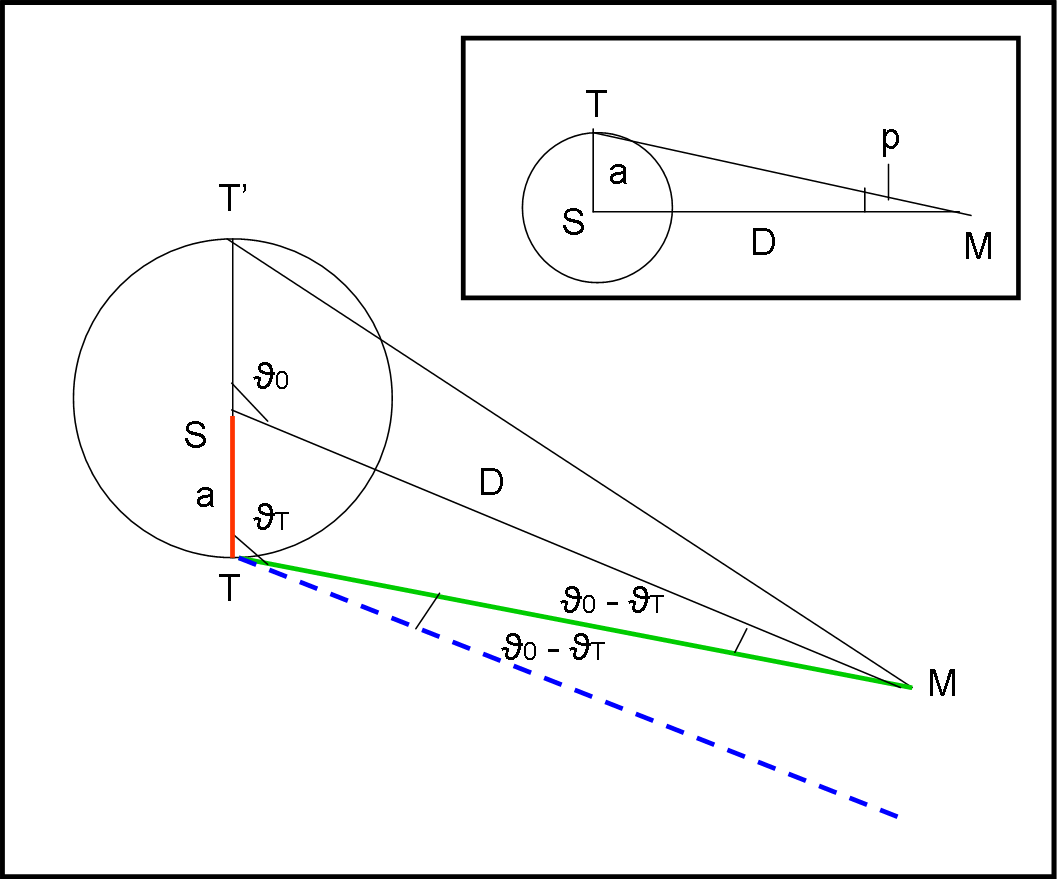
Applicando il teorema dei seni (il rapporto tra i seni di due angoli è uguale al rapporto tra i lati opposti) si ottiene:
D/sen ϑT = a/sen (ϑ0 - ϑT)
sen (ϑ0 - ϑT) = (a/D) sen ϑT …. (1)
Definiamo parallasse annua della stella M l’angolo p tale che:
tan p = a/D (vedi riquadro nella Fig. 18)
Essendo p sempre molto piccolo (inferiore al secondo d’arco) si può assumere:
tan p = p = a/D
Questa è la classica definizione di parallasse annua di una stella M.
Torniamo alla (1) ed eseguiamo qualche altra approssimazione più che ammissibile vista la piccola differenza tra ϑ0 e ϑT.
sen (ϑ0 - ϑT) = p sen ϑT
ϑ0 - ϑT = p sen ϑ0 …. (2)
Questa è la formula fondamentale che ci permette di calcolare la parallasse nel quarto sistema di coordinate celesti. Un esercizio che potrebbe sembrare inutile, ma che è della massima importanza per una trattazione “concreta”.
Disegniamo, in Fig. 19, la sfera celeste tracciando sia i cerchi massimi dell’equatore che dell’eclittica.
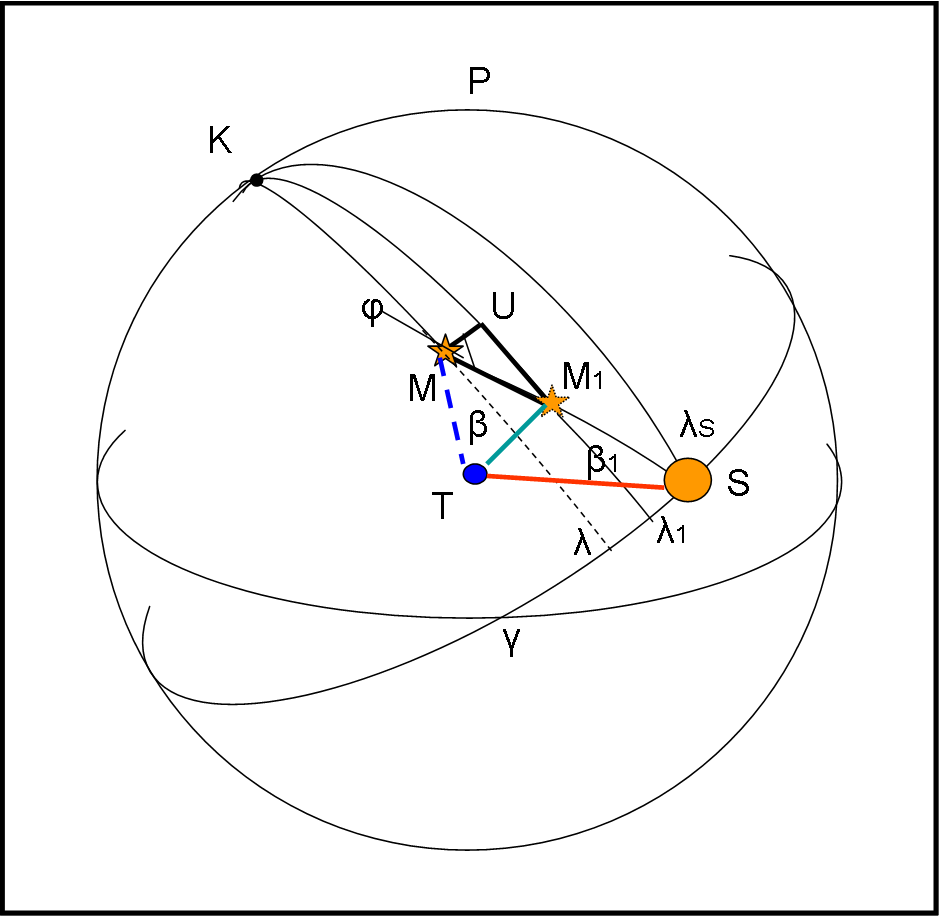
T sia al centro della sfera (condizioni geocentriche) e S sia la posizione del Sole lungo l’eclittica. M sia la posizione eliocentrica della stella (angolo ϑ0). M1 è invece la posizione della stella vista dalla Terra (angolo ϑT ). Per quanto detto precedentemente (basta guardare la Fig. 18 e pensare di prendere quel piano e portarlo nella Fig. 19). M1 deve stare sullo stesso piano di S, di T e di M, dato che è la posizione di M vista dalla terra. Ne segue che M1 deve stare sul cerchio massimo che passa da S e M. Diciamo le stesse cose con maggiore semplicità. Prendiamo il piano di Fig. 18 e segniamo le direzioni che ci interessano a partire da T. Abbiamo la direzione TS, la direzione TM che dà luogo alla posizione M1, la direzione tratteggiata parallela a SM che da luogo a TM. Queste tre direzioni devono stare su un piano e quindi su un cerchio massimo che passa per S, pr M1 e M. In altre parole ancora: il triangolo curvilineo di vertice T e che ha come lato opposto curvilineo il cerchio massimo SM1M non è altro che il piano di Fig. 18.
Da M tracciamo un arco di cerchio minore parallelo all’eclittica fino al cerchio massimo che passa per M1. Chiamiamo U il punto intersezione.
Attraverso la trigonometria sferica e i sistemi di coordinate celesti siamo in grado di risolvere il problema cominciando dal triangolo MM1U (attenzione che non è un triangolo sferico, dato che UM non è un cerchio massimo e, quindi, intrinsecamente UM è una curva e non un lato “sferico rettilineo” come UM e MM1). I sui lati, però, sono molto piccoli e possiamo anche trattarlo come un triangolo piano.
Chiamiamo le cose con il loro nome. Le coordinate della stella M siano λ e β, mentre quelle di M1 siano λ1 e β1 (longitudine e latitudine, rispettivamente). L’angolo UMM1 lo indichiamo con φ.
Possiamo scrivere (QUI, Fig. 15) che:
UM = (λ1 – λ) cos β
Ma anche che:
UM = MM1 cos φ
Ponendo
λ1 – λ = Δλ e β1 - β = Δβ
Abbiamo:
UM = Δλ cos β = MM1 cos φ …. (3)
UM1 è dato da:
UM1 = - Δβ = MM1 sen φ …. (4)
Tuttavia, sappiamo anche che (ricordandoci il piano di Fig. 18, che si trasferisce nell'arco di cerchio massimo MM1S)
MM1 = ϑ0 - ϑT
MS = ϑ0
Da cui, la (3) e la (4) diventano:
Δλ cos β = (ϑ0 - ϑT) cos φ
- Δβ = (ϑ0 - ϑT) sen φ
E, ancora, ricordando la (2):
Δλ cos β = p sen ϑ0 cos φ …. (5)
Δβ = - p sen ϑ0 sen φ …. (6)
Passiamo a un triangolo sferico “vero”: KMS
MKS = λS – λ
KS = 90°
KM = 90° - β
KMS = 90° + φ
MS = ϑ0
Applicando la seconda formula fondamentale (QUI insieme alla terza) si ha:
sen ϑ0 /sen (λS – λ) = sen (90)/sen (90° + φ)
sen ϑ0 sen (90° + φ) = sen (λS – λ)
sen ϑ0 cos φ = sen (λS – λ) …. (7)
Applicando la terza formula fondamentale, si ha:
sen ϑ0 cos (90° + φ) = cos (90°) sen (90° – β) - cos (90° – β) sin (90°) cos (λS – λ)
- sen ϑ0 sen φ = - sen β cos (λS – λ)
sen ϑ0 sen φ = sen β cos (λS – λ) …. (8)
Sostituendo la (7) e la (8) nella (5) e nella (6)
Si ottiene:
Δλ cos β = p sen (λS – λ) …. (9)
Δβ = - p sen β cos (λS – λ) …. (10)
Possiamo permetterci di indicare UM con x e dalla (3) e dalla (9), si ha:
x = p sen (λS – λ) spostamento parallelo all’eclittica …. (11)
e indicare UM1 con y e dalla (4) e (10), si ha
y = p sen β cos (λS – λ) spostamento perpendicolare all’eclittica …. (12)
Possiamo scriverle:
x/p = sen (λS – λ)
y/p sen β = cos (λS – λ)
Quadrando e sommando, si ottiene:
x2/p2 + y2/(p sen β)2 = sen2(λS – λ) + cos2(λS – λ)
x2/p2 + y2/(p sen β)2 = 1 equazione dell'ellisse parallattica
Che non è altro che l’equazione di un’ellisse che ha il semiasse maggiore sempre uguale alla parallasse della stella, mentre quello minore varia con la latitudine. Se essa è 90° (stella nel polo dell’eclittica) il semiasse minore diventa p e quindi l’ellisse diventa un cerchio. Se è 0°, stella sull’eclittica, l’ellisse degenera in un trattino lungo la stessa eclittica.
Potrebbe sembrare un qualcosa di “noiosamente” matematico, ma il risultato è estremamente interessante e dimostra elegantemente e compiutamente le caratteristiche dell’ellisse parallattica.
Ciò che abbiamo fatto per la parallasse può essere ripetuto per l’aberrazione annua.
Aberrazione annua
Ripetiamo ciò che capita in realtà, utilizzando il nostro telescopio di obiettivo O e di fuoco F (non fa mai male ribadire certi concetti facili a ritornare confusi).
I raggi luminosi paralleli giungono a noi dalla stella M (Fig. 20).
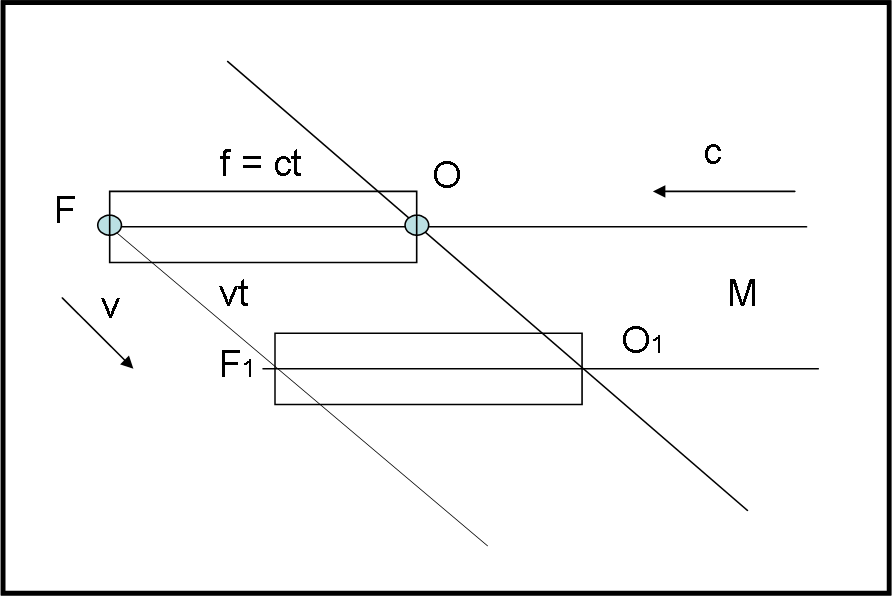
Il fotone azzurro tocca l’obiettivo O. Tuttavia se il telescopio è diretto verso la stella, nel tempo t (v è la velocità orbitale terrestre) esso si è spostato parallelamente a se stesso nella posizione O1F1 Nello stesso tempo t, il fotone azzurro ha proseguito la sua corsa e percorre la lunghezza del telescopio f = ct, giungendo nella posizione del vecchio fuoco F, dove non c’è più niente e nessuno ad aspettarlo. L’osservazione è fallita!
Nessun problema. Basta puntare il telecopio nella direzione FO1 (Fig. 21) e la luce del fotone arancione viene catturata! Infatti nel tempo t che il telescopio impiega per spostarsi da FO1 in F1O2 , il fotone arancione passa da O1 a F1 (lui viaggia in linea retta). L’osservazione è riuscita!
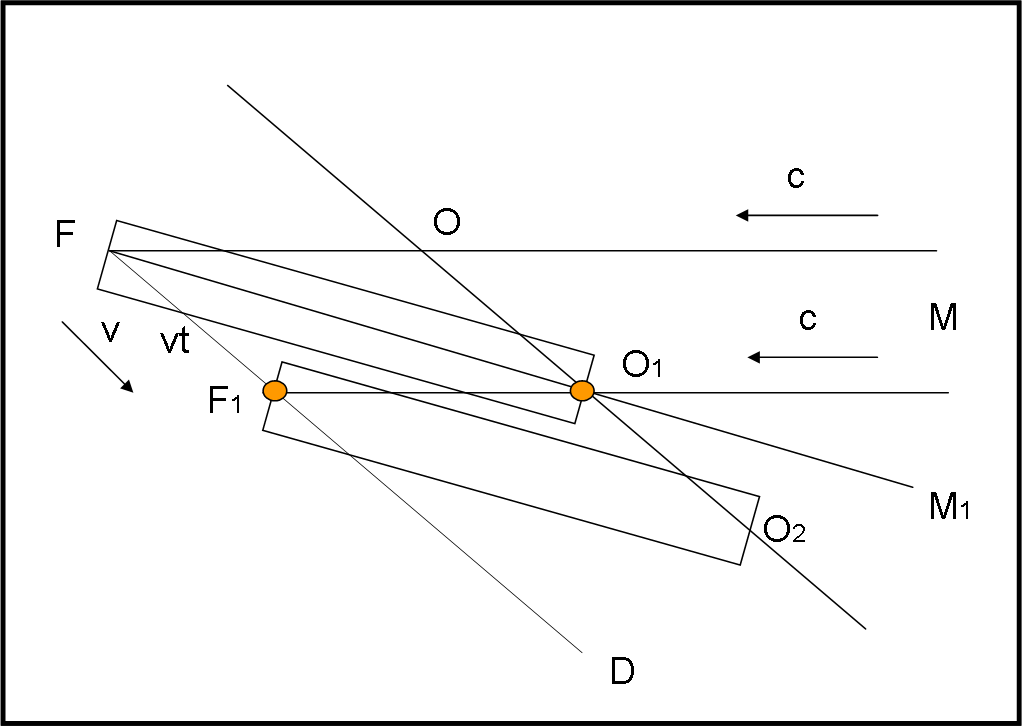
Ma vediamo, grazie a questa animazione papallicola, cosa accade al fotone sia nel caso descritto nella fig. 20 che in quello della fig. 21 (grazie Paolino! ![]() )
)
In base al piccolo riassunto possiamo passare tranquillamente a una descrizione puramente geometrica della situazione, dando un nome ai vari angoli che partecipano al fenomeno (Fig. 22).
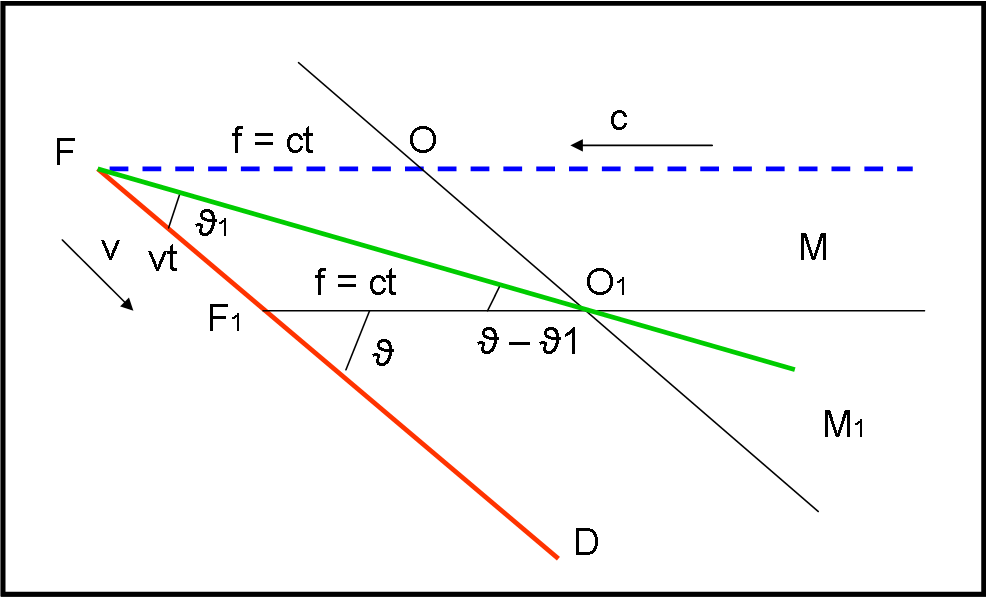
Consideriamo il triangolo FF1O1. L’angolo ϑ è l’angolo effettivo tra direzione della stella e lo spostamento lungo l’orbita terrestre, mentre ϑ1 è l’angolo che l’asse del telescopio deve fare con la direzione del moto terrestre. La loro differenza ci dice di quanto il telescopio vada inclinato e coincide con l’angolo sotto cui l’obiettivo O1 vede il fuoco F e il fuoco F1, ossia la distanza vt (angoli alterni interni di rette parallele tagliate da una trasversale).
Possiamo applicare il teorema dei seni e scrivere:
vt/sen(ϑ – ϑ1) = ct/sen ϑ1
ossia:
sen(ϑ – ϑ1) = (v/c) sen ϑ1
Questa formula ci dice già un paio di cose molto importanti, che incontreremo in seguito: compare il rapporto v/c, il che fa cadere automaticamente il fenomeno nella relatività ristretta; non abbiamo usato composizioni di vettori velocità, ma solo distanze percorse in un certo tempo t e quindi la costanza della velocità della luce non è messa in dubbio. Risulta chiaro che il fenomeno deve essere trattato nella RR qualora v sia comparabile con c (e quindi la eventuale somma di velocità dovrà cambiare), ma può trattarsi in modo classico quando v << c. Non preoccupiamoci più di tanto, quindi, e andiamo avanti in modo classico dato che v è decisamente minore di c e non stiamo commettendo nessun errore significativo. Ricordiamo solo che la formula dovrà cambiare nella RR...
Data la piccolezza di v/c (dell’ordine di 10-4), si possono fare le solite approssimazioni. Sostituiamo il seno di ϑ – ϑ1 con l’angolo e al posto del seno di ϑ1 possiamo scrivere ϑ:
ϑ – ϑ1 = (v/c) sen ϑ
Trasformando tutto in secondi d’arco, v/c assume il valore fisso di 20”.5 e viene chiamata costante di aberrazione K, ossia:
ϑ – ϑ1 = K sen ϑ …. (13)
Non ci resta, adesso, che vedere cosa capita nella sfera celeste e, in particolare, nel quarto sistema di coordinate.
Prima, però, vediamo in Fig. 23, uno schema dell’orbita terrestre, supposta circolare.
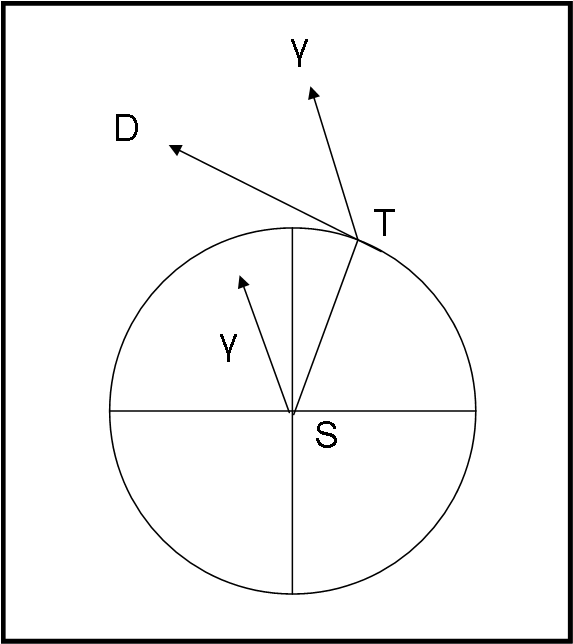
La terra T (dove sistemeremo il centro della sfera celeste) si muove in direzione di D. Questa direzione è perpendicolare alla direzione del Sole S. Sia Tγ la direzione del punto gamma o d’Ariete, da cui si misurano le longitudini. Ne segue che la longitudine geocentrica del Sole è data dall’angolo γTS, mentre quella della direzione D (γTD) è 90° più piccola, ossia vale la relazione
λD = λS – 90°
Questa semplice relazione non dice altro che la direzione importante non è più quella del Sole ma quella della direzione del moto della Terra che formano, tra loro, un angolo di 90° (posizione e velocità…).
Passiamo alla sfera celeste e utilizziamo, in Fig. 24, esattamente la stessa figura (Fig. 19) usata per la parallasse.
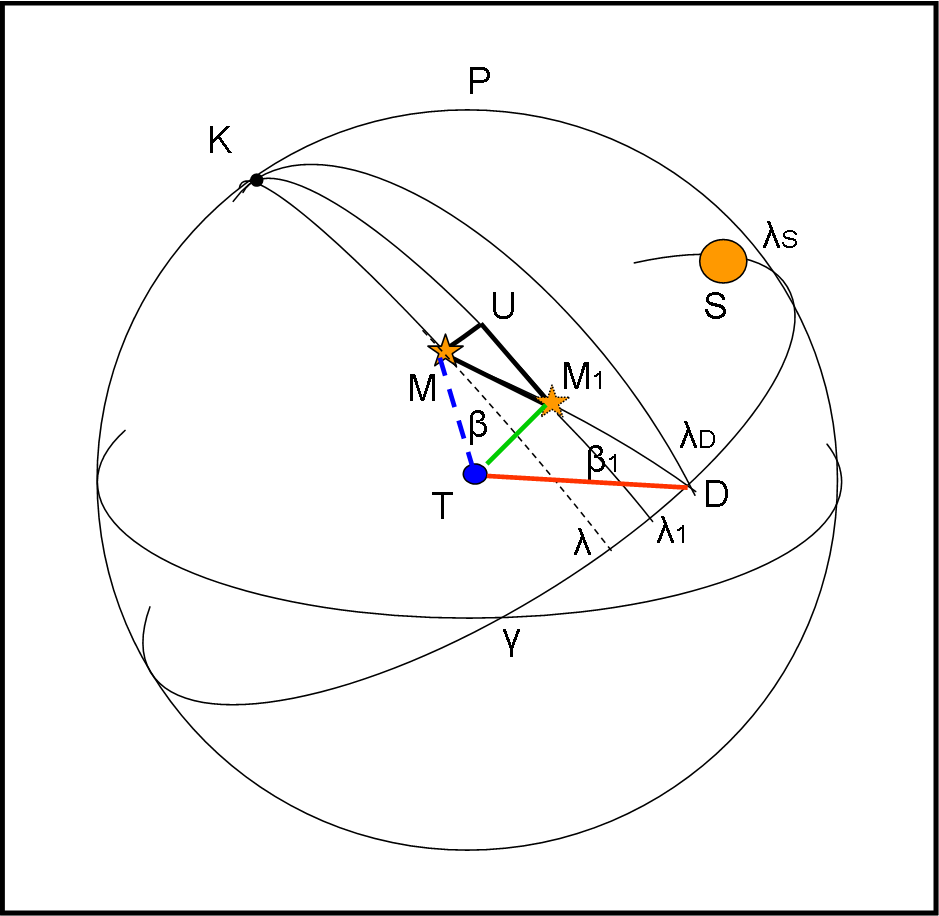
M è la stella come vista dal Sole e M1 come è vista dalla Terra: il piano di riferimento è, adesso, MTD, il che comporta che il cerchio MM1D sia un cerchio massimo, quello in cui avviene lo spostamento della stella. Gli unici cambiamenti sono:
(1) Consideriamo λD al posto di λS
(2) L’angolo ϑ – ϑ1 prende il posto di ϑ0 - ϑT, il che vuol dire che al posto di p inseriamo K
A questo punto potete proseguite da soli, ripetendo quanto fatto precedentemente per la parallasse (un esercizio veramente banale). Si ottiene (tanto per dare un aiuto…):
x = Δλ cos β = K sen ϑ cos φ = - K cos (λS – λ)
y = Δβ = - K sen ϑ sen φ = - K sen β sen(λS – λ)
x/K = - cos (λS – λ)
y/K sen β = sen(λS – λ)
Quadrando e sommando:
x2/K2 + y2/K2sen2β = 1 equazione dell'ellisse di aberrazione
Che è nuovamente l’equazione di un'ellisse che ha come semiasse maggiore K e come semiasse minore Ksen β. Per una stella sull’eclittica l’ellisse si riduce a una linea che la stella percorre avanti e indietro, mentre per una stella nel polo dell’eclittica l’ellisse diventa una circonferenza di raggio K. Questo vale per tutte le stelle del firmamento e quindi il semiasse maggiore, essendo una costante, è uguale per tutte le stelle.
Bene, la parte più noiosa è terminata (ma tutti gli astrofili, almeno, dovrebbero impararla per sapere cosa vedono realmente sulla sfera celeste). La prossima volta entreremo prepotentemente nei due sistemi di riferimento per generalizzare il problema dell’aberrazione e vederla veramente come effetto relativistico. Ci faremo aiutare da una storia mitologica…







3 commenti
Ebbene sì, cari amici... ormai i papallicoli riescono a entrare e uscire dagli articoli e farti dei regali eccezionali !!
Uno si sveglia alla mattina e si trova delle fantastiche animazioni che spiegano perfettamente l'aberrazione.
GRAZIE PAOLO!!!!! (mi sa che ci sia anche lo zampino di Scherzy... sembra cattivo, ma deve essere un buono, in fondo, in fondo...).
Quando si dice collaborazione a 360°.... e ne vedrete delle belle....
Mi sa che sono troooooppo buono! Deve essere colpa dell'atmosfera inquinata di questo strano pianeta o del riscaldamento globale, chissà...
Ho appena sostituito l'animazione che hai visto stamani con quella ancora più completa che mi ha mandato Paolino Papallicolo... all'inizio è uguale, ma poi c'è qualcosa in più!
ops... credevo fosse la stessa ... rigrazie Paolino e anche Scherzy (a denti stretti!).