Categorie: Astronomia Elementare
Tags: allineamenti planetari opposizioni periodo sinodico risonanze
Scritto da: Vincenzo Zappalà
Commenti:0
Allineamento planetario: come, quando, perché!
Questo articolo è inserito nella pagina d'archivio dedicata all'Astronomia Classica
Non accadeva da 18 anni e dovremo attenderne altrettanti per poter di nuovo ammirare uno spettacolo del genere...
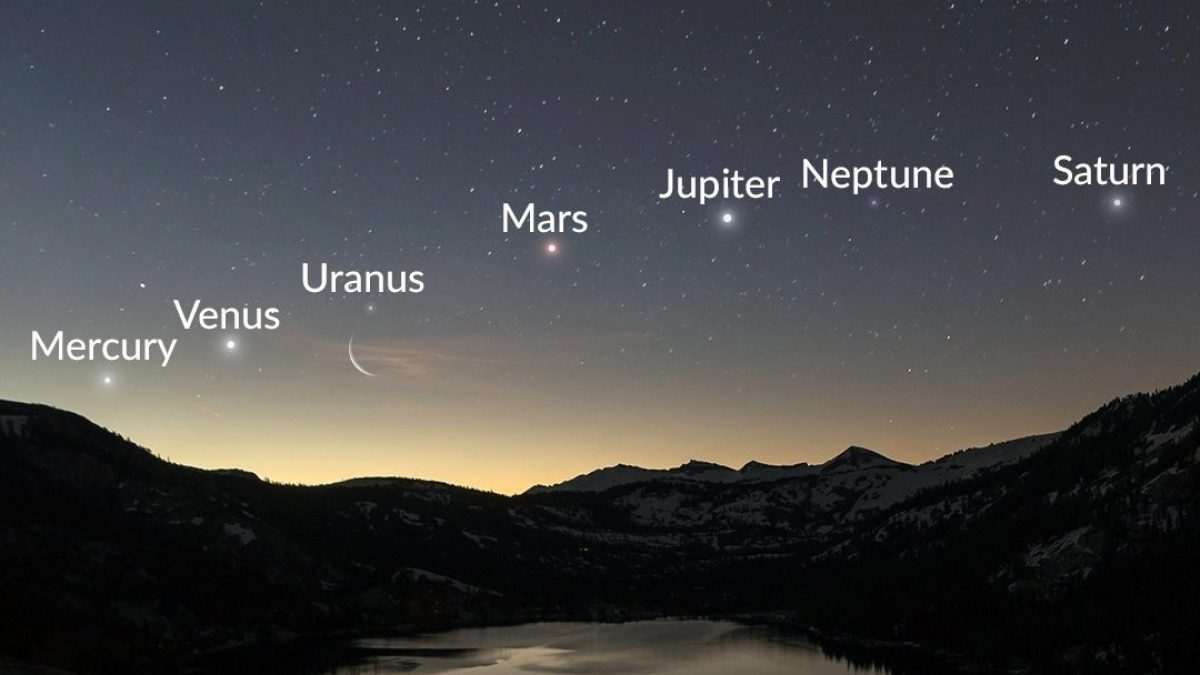
Ma cos'è successo nel cielo?
Tutti i pianeti si sono trovati dalla stessa parte rispetto al Sole rischiando di "sbilanciarlo" gravitazionalmente e di farlo precipitare nel buco nero galattico? La rara configurazione astrale garantirà vincite alla lotteria ai nati sotto il segno dei pesci e grandi mal di testa agli scorpioni? Ovviamente no.
Spacchiamo, dunque, il capel... ops... il pianeta in quattro ed esaminiamo in dettaglio cosa si intende per allineamento planetario!
E se qualcuno tra voi lettori è riuscito a scattare una bella foto e ha piacere di inviarcela, può farlo scrivendo una mail a infinitoteatrocosmo@gmail.com. Vincerà un bel... niente (tanto per cambiare), ma avrà la soddisfazione di consegnare alla memoria dei posteri la sua foto, che verrà pubblicata nel blog più infinito dell'Universo conosciuto.
Segue l'articolo pubblicato il 2/1/2017
Allineamento planetario: gioia e dolore di molti astrofili. In realtà, spesso e volentieri si fa molta confusione riguardo all’allineamento dei pianeti. Soprattutto, quando lo si vuole riferire a episodi catastrofici di tipo gravitazionale o mareale.
Si legge spesso che tutti i pianeti posizionati dalla stessa parte del Sole potrebbero sconvolgere l’intero Sistema Solare e la Terra con lui. Una specie di bilancia che vedrebbe da un lato il Sole, da solo, e dall’altro tutti i suoi figlioli. Beh… sappiamo bene che anche se si verificasse questa configurazione non succederebbe assolutamente niente, date le masse e le distanze in gioco. Non vogliamo certo perdere tempo con queste fesserie da catastrofisti ignoranti e/o da astrologi furbacchioni.
Resta comunque una grande confusione riguardo al significato di allineamento planetario. Normalmente, il problema sorge quando un pianeta si vede prospetticamente vicino a qualche altro e si ha una congiunzione estremamente suggestiva e fotografata. Il fascino resta indubbio, ma si dovrebbe fare anche molta chiarezza. Probabilmente nessuno dei lettori di questo circolo ha mai subito questo tipo di turbamento, ma è bene partire proprio da zero per poi passare a discorsi più sensati sia matematicamente che geometricamente e –magari- anche fisicamente.
In linea di massima l’allineamento apparente di più pianeti rimette in moto i catastrofisti della “bilancia” gravitazionale. Ciò sembrerebbe indicare, quantomeno, che come allineamento s’intende la situazione in cui i pianeti stiano tutti dalla stessa parte rispetto al Sole, se visti dalla Terra (il nostro punto di osservazione). In tal caso, però, nasce subito un grave errore interpretativo. Tra i pianeti "vicini" nel cielo vi è quasi sempre Venere e/o Mercurio, oltre a qualcuno esterno, come Marte o Giove o Saturno. Beh… in questo caso NON possiamo essere assolutamente nelle condizioni di pianeti che stanno tutti dalla stessa parte!
Ricordiamo (scusatemi...), infatti, che Mercurio e Venere rivolvono all’interno dell’orbita terrestre, mentre gli altri all’esterno. E’ perciò impossibile vederli tutti vicini nel cielo se sono posizionati dalla stessa parte rispetto al Sole. Quelli interni, nel caso di questo tipo di allineamento, starebbero a 180° rispetto agli altri e non potremmo certo vederli vicini a loro. Ripeto ancora: se vediamo Venere e Marte e/o Giove vicini nel cielo ci troviamo in una configurazione di allineamento che niente ha a che vedere con la bilancia tanto temuta.
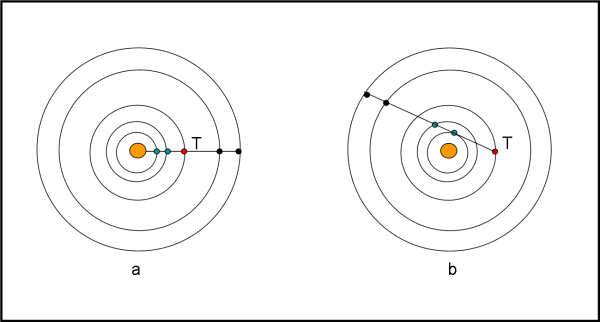
Bastano due semplici figure per capire il succo del discorso. Nella Fig. 1a abbiamo tutti i pianeti (immaginiamo un sistema planetario con solo 5 pianeti) allineati rispetto al Sole. La Terra è il punto rosso. E’ chiaro, in questo caso, che la Terra non può assolutamente vedere tutti i pianeti vicini nel cielo. Se invece vogliamo proprio vedere tutti i pianeti vicini, dobbiamo considerare un diverso tipo di allineamento, come quello mostrato in Fig. 1b. Tuttavia, in questo caso l’effetto bilancia "catastrofico" non ha più alcun senso.
Scusate, se ho fatto un discorso quasi infantile, ma, spesso, leggendo in altri blog le domande sull’allineamento planetario, sembra proprio che questa netta differenza non sia capita molto bene. La faccenda viene, anzi, peggiorata, dato che alle domande sul possibile allineamento dei pianeti (sì, ma quale tipo di allineamento?), la risposta è sempre la stessa: “Fai girare uno dei soliti programmini precotti, come Stellarium (utilissimo per chi già sa) e troverai le prossime congiunzioni, opposizioni o allineamenti vari”. Il solito metodo “moderno” che dà risposte più o meno utili “praticamente”, senza però affrontar minimamente il concetto geometrico o matematico o fisico che vi sta dietro: nozioni da imparare a memoria, eliminando qualsiasi comprensione più che doverosa per chiunque.
Bene, cari amici, vogliamo proprio investigare e chiarire un po’ meglio le problematiche che stanno dietro all’allineamento dei pianeti, se visti da un pianeta come la Terra. Vedremo che si possono anche trovare formule semplici per prevedere i prossimi allineamenti, sia in un caso che nell’altro. Tuttavia, per non passare a calcoli di meccanica celeste (quella VERA e non quella che riguarda i fenomeni geometrici apparenti) ultra complessi, dovremo accontentarci di orbite circolari e complanari, ossia dovremo escludere orbite eccentriche e inclinate e trascurare del tutto le perturbazioni reciproche, che portano a fenomeni come la precessione orbitale e molte altre cose ancora più sofisticate (meccanismi di protezione e risonanze di ordine superiore, ad esempio).
Già con queste limitazioni, il problema non è proprio banale e necessità una chiara comprensione del periodo siderale e sinodico e di come essi debbano essere legati tra loro. Un gioco essenzialmente geometrico e matematico, in cui la fisica si tiene un po’ in disparte.
Periodo sinodico
L’esistenza di risonanze di moto medio può essere gioia e dolore per chi cerca di ottenere allineamenti non solo frequenti, ma addirittura periodici, soprattutto nei satelliti gioviani (i più fotografati e seguiti). Ricordiamo ancora che, mettendoci nel caso di orbite perfettamente circolari e complanari, eliminiamo i vari effetti mareali e trascuriamo quelli dovuti a eventuali perturbazioni reciproche, anche se debolissime.
Prima di analizzare qualche semplice caso, come quello dei primi tre satelliti galileiani, introduciamo un periodo particolarmente importante: il periodo sinodico di un pianeta rispetto a un altro.
Esso è fondamentale, dato che è l’unico che può essere osservato direttamente.
Consideriamo la Terra e Marte, per esempio. Conosciamo il periodo siderale della Terra (ossia quello effettivo di rivoluzione attorno al Sole) attraverso osservazioni che ci permettano di vedere una certa stella lontana nella stessa posizione precedente. L’intervallo di tempo tra le due osservazioni ci regala il periodo di rivoluzione intorno al Sole (vi sono anche altri periodi, ma che -per adesso- possiamo tralasciare).
Non avendo ancora mandato uomini su Marte, non possiamo aspettarci che essi ci diano la stessa informazione dal pianeta rosso. Tutto ciò che possiamo fare è osservare quando Marte si viene ad allineare perfettamente con noi e il Sole (ossia si trova all’opposizione). L’intervallo di tempo tra due opposizioni, ossia tra due allineamenti, prende proprio il nome di periodo sinodico.
Senza bisogno di sapere le leggi di Keplero, basta questa informazione per ricavare il periodo di rivoluzione di Marte attorno al Sole.
Disegniamo la semplice Fig. 2.
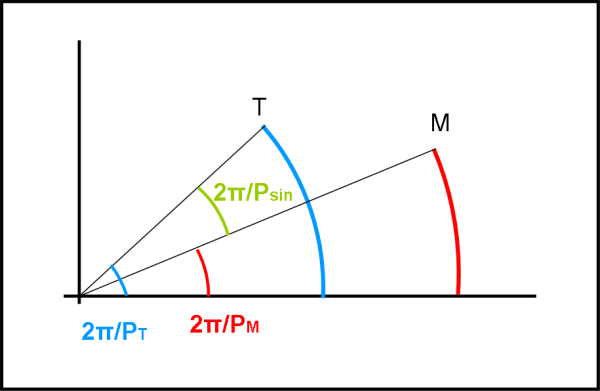
La Terra rivolve più velocemente di Marte e, nel caso di orbita circolare, possiamo scrivere che la sua velocità angolare è costante e vale 2π/PT. Velocità angolare non vuole dire altro che angolo percorso nell’unità di tempo. Marte, più lento, nella stessa unità di tempo ha, invece, una velocità angolare data da 2π/PM. La Terra lascia Marte dietro di sé e inizia il suo giro attorno al Sole fino a compierlo completamente. E’ passato un tempo PT.
Ovviamente, però, in quella posizione, Marte non si troverà più nella stessa posizione dell’anno precedente. Anche se più lentamente si è spostato nella sua orbita. La Terra, per raggiungerlo deve allora percorrere un certo angolo supplementare. In altre parole, per ritrovarsi allineata con Marte e Sole deve girare ancora un po’. Di quanto deve girare? Proprio della differenza tra il suo angolo percorso nell’unità di tempo e quello percorso nell’unità di tempo da Marte. Questo angolo corrisponde al movimento della Terra relativo a Marte ed è proprio dato da 2π/Psin, dove Psin è l’intervallo di tempo necessario alla Terra per ritrovarsi allineata con Marte e il Sole, ossia l’intervallo tra due opposizioni, o -ancora- il periodo sinodico di Marte relativo alla Terra. Si può scrivere la banale formula:
2π/Psin,M = 2π/PT - 2π/PM …. (1)
Conoscendo PT e osservando Psin si può ricavare PM
Se, invece, applicassimo lo stesso tipo di procedimento a un pianeta interno come Venere, ci troveremmo di fronte a un cambiamento di segno. Venere va più forte della Terra. La formula precedente diventa:
2π/Psin,V = 2π/PV - 2π/PT …. (2)
Ovviamente, per due pianeti si ha sempre un allineamento (o esterno o interno) a ogni periodo sinodico.
Torniamo a Marte e immaginiamo, adesso, di aggiungere un terzo pianeta, per esempio Giove. La formula precedente ci permette di sapere quando avverrà un futuro allineamento tra Terra e Giove. Tuttavia, dopo un periodo sinodico di Marte NON ci sarà sicuramente Giove allineato, dato che il suo periodo sinodico è diverso. L’unica cosa da sperare è che a furia di girare attorno al Sole succeda che un multiplo esatto del periodo sinodico di Marte coincida perfettamente con un multiplo esatto del periodo sinodico di Giove. Ossia è necessario che trascorra un tempo t dato da:
t = m Psin,G = n Psin,M …. (3)
con m e n numeri INTERI. (N.B.: E se non lo fossero mai…?)
Risonanze orbitali
Bene, abbiamo già anticipato in parte il risultato finale, in modo molto formale, e possiamo tornare all’inizio e considerare il caso di pianeti o satelliti (o quello che volete) con periodi che stanno in risonanza tra loro. Questo già ci assicura che i periodi stanno tra loro come numeri interi semplici. Prendiamo quella forse più famosa che è la risonanza di Laplace, ossia tale che il rapporto tra i periodi di rivoluzione di tre oggetti celesti stiano tra loro come i numeri 1, 2 e 4. Siamo nel caso di Io, Ganimede e Europa
I tre satelliti di Giove hanno periodi PI, PE e PG tali che:
PI/PE = 1/2
PI/PG = 1/4
Consideriamo come unità di misura del tempo il periodo di rivoluzione di Io attorno a Giove. Per cui
PI = 1
PE = 2
PG = 4
D’ora in poi, per una necessità di semplicità che risulterà evidente più in là, assumiamo che all’istante iniziale (t = 0) i tre oggetti siano perfettamente allineati.
La domanda è: “Dopo quanto tempo torneranno a essere allineati?”
Il caso è talmente semplice che possiamo risolverlo graficamente, come mostrato in Fig. 3.
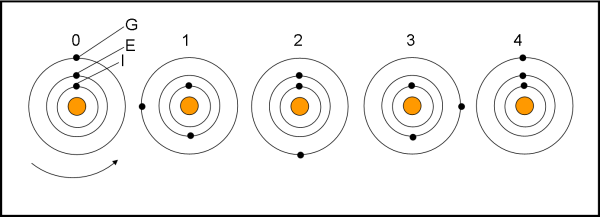
Dopo un giro esatto di Io, Europa si trova allineata in direzione opposta rispetto a Giove, avendo percorso solo 1/2 della sua orbita, e Ganimede spostato verso sinistra (in quadratura) avendo percorso solo 1/4 della sua orbita. Dopo due rivoluzioni di Io, Europa torna a essere allineata con lui dalla stessa parte di Giove, mentre Ganimede si trova a 180°. Dopo tre rivoluzioni Io ed Europa si trovano in posizioni opposte rispetto a Giove e Ganimede spostato verso destra. Alla quarta rivoluzione di Io tutto torna esattamente com’era all’istante 0. Ne segue che sono necessarie quattro rivoluzioni di Io per riottenere l’allineamento. Va notato che abbiamo semplificato l’intera faccenda avendo trascurato la pur piccola eccentricità orbitale e la precessione del perielio. Ma per i nostri scopi possiamo permetterci questo e altro.
L’intervallo t tra due allineamenti dei tre oggetti, dalla stessa parte rispetto a Giove, è dato quindi da:
t = 4 rivoluzioni di Io
Possiamo ottenere lo stesso risultato senza bisogno di fare figure che potrebbero diventare lunghissime cambiando il tipo di risonanza? Sicuramente sì: basta ricordare la (1) e la (3), ossia utilizzare i periodi sinodici.
Determiniamo i periodi sinodici di Europa e Ganimede rispetto a Io. Consideriamo ancora come unità di tempo il periodo di rivoluzione di Io. La (1) ci dice:
2π/Psin,E = 2π/PI - 2π/PE
1/ Psin,E = 1/1 – 1/2
1/Psin,E = 1/2
Psin,E = 2
1/Psin,G = 1 – 1/4
Psin,G = 4/3
Ovviamente, per come è definito, il periodo sinodico di un oggetto, più lontano e più lento, risulta più corto di quello di un oggetto più vicino e veloce. Se l’oggetto lontano fosse praticamente fermo, il periodo sinodico sarebbe praticamente uguale al periodo di Io.
Ricordando la (3), per avere un nuovo allineamento, deve essere:
m Psin,G = n Psin,E …. (4)
m 4/3 = n 2
m/n = 2·3/4 = 6/4 = 3/2
Esistono due numeri interi m e n tali che sia soddisfatta la relazione (4)? Sì, e i più piccoli sono proprio:
m = 3
n = 2
Ne segue che l’intervallo di tempo tra due allineamenti dei tre satelliti sarà dato da:
t = 3 Psin,G = 2 Psin,E = 3·4/3 = 2·2 = 4 periodi di rivoluzione di Io
Come volevasi dimostrare
Fate pure altri casi particolari per prendere dimestichezza con il periodo sinodico. Magari, potreste calcolarvi i periodi sinodici di tutti i pianeti rispetto alla Terra oppure i periodi sinodici di tutti i pianeti rispetto a Nettuno. Vedremo che sarà necessario fare come Taylor, ossia cercare di ottenere il tempo t con approssimazioni successive.
Consideriamo il caso ipotetico in cui la risonanze tra Io ed Europa sia 1/2 e quella tra Io e Ganimede 1/3. Potete, ovviamente, trovare il periodo di allineamento eseguendo una figura simile a quella precedente. Noi, però, continuiamo a lavorare con i periodi sinodici.
PI = 1
PE = 2
PG = 3
Psin,E = 2 (come prima…)
1/Psin,G = 1 – 1/3 = 2/3
Psin,G = 3/2
Deve essere:
m 3/2 = n 2
m/n = 4/3
esistono due numeri interi che soddisfano la relazione? Sì e sono:
m = 4
n = 3
t = 3·2 = 4·3/2 = 12/2 = 6 periodi di Io
Tutto risolto? Non proprio…
Torniamo al caso reale dei tre satelliti (risonanza di Laplace). Cosa succederebbe se non li facessimo partire allineati all’istante t = 0 ? La situazione potrebbe essere senza speranza, proprio perché esiste la risonanza di Laplace. Se, ad esempio, quando Io ed Europa fossero allineati si mettesse Ganimede spostato a sinistra, potreste far girare quanto volete i satelliti ma non si otterrebbe mai un allineamento completo, ma solo a due a due. Le risonanze causano il ripetersi continuo e periodico di configurazioni identiche e quindi la configurazione iniziale diventa essenziale. In certi casi si favorisce l’allineamento e in altri lo si esclude del tutto. Il caso di Io, Europa e Ganimede è proprio di quelli senza speranza e i tre satelliti non si allineano mai. Che cosa ha causato questo sfasamento? Beh… bisognerebbe risalire alla loro origine e ai meccanismi di protezione che hanno operato nelle prime fasi. Ma questo è qualcosa di estremamente più difficile da sapere!
Avanti con i pianeti
Restiamo allora nel nostro Sistema Solare semplificato e vediamo di applicare ad altri pianeti il tipo di analisi che abbiamo appena imparato. Tanto per non farci mancare niente, consideriamo questa volta i pianeti interni, Mercurio e Venere. In questo caso, però, i periodi di rivoluzione di Mercurio, Venere e Terra non stanno più tra di loro come numeri semplici, ossia non sono in risonanza.
Tuttavia, cerchiamo di approssimare la situazione reale partendo da un situazione ipotetica che dia luogo a risonanze, per poi migliorarla con passi successivi. Un metodo operativo che ci permetterà di capire meglio a cosa andiamo incontro quando si vuole estendere l’allineamento a pianeti con periodi qualsiasi e in numero maggiore di tre.
Quanto vale il periodo orbitale di Mercurio? Presto detto: 87.96 giorni che approssimiamo a 88 giorni. E quello di Venere? 224.70 giorni che approssimiamo a 225. Quello della Terra è ovviamente 365 giorni.
Partiamo da lontano e scriviamo un rapporto di numeri interi (il più semplice possibile) che si avvicini a 88. Scegliamo 1/4, ossia ipotizziamo che Mercurio abbia un periodo che sia 1/4 di quello della Terra. Ciò vuole dire considerare il periodo di Mercurio uguale a 91 giorni circa. Piuttosto approssimato, ma per cominciare va più che bene.
Passiamo a Venere. Bene, scegliamo 2/3 che ci regala 243 giorni. Non è poi così lontano da quello reale… Possiamo partire con i nostri calcoli.
La situazione è la seguente:
PM/PT = 1/4
PV/PT = 2/3
con PT = 1, i valori precedenti ci danno i periodi di Mercurio e Venere espressi in anni terrestri.
Calcoliamo i periodi sinodici con la (2), dato che i pianeti sono interni.
1/Psin,M = 1/PM – 1/PT = 1/1/4 – 1 = 4 -1 = 3
Psin,M = 1/3
1/Psin,V = 1/2/3 – 1 = 3/2 – 1 = 1/2
Psin,V = 2
Non stupitevi se il periodo sinodico di Venere è maggiore dell’anno terrestre. E’ vero che va più veloce, ma per riuscire a raggiungere la Terra, che comunque si muove, deve passare più di un anno.
La relazione (3) diventa:
m 2 = n 1/3
m/n = 1/(3·2) = 1/6
m = 1
n = 6
t = 1·2 = 6 ·1/3 = 2 anni terrestri
Accidenti! Che meraviglia… avremmo una congiunzione Mercurio e Venere ogni due anni. Inoltre, dato che le orbite sono supposte complanari, avremmo un transito di Venere e nello stesso momento un transito di Mercurio, con Venere che ci nasconderebbe Mercurio… Beh, purtroppo è solo un’approssimazione esagerata. Cerchiamo di fare qualcosa di meglio…
Continuiamo, comunque, ad approssimare i periodi di Venere e Mercurio, in modo che diano rapporti di numeri interi rispetto al periodo della Terra. E’ facile capire perché: solo in questo modo riusciremo a trovare multipli di periodi sinodici che possano uguagliarsi…
Scegliamo due frazioni meno semplici: 7/30 per Mercurio e 13/21 per Venere.
Questo vorrebbe dire che il periodo siderale di Mercurio sarebbe di 85 giorni. Non molto meglio di prima, ma accontentiamoci… Quello di Venere risulterebbe, invece, pari a 226 giorni, decisamente un’ottima scelta!
Calcoliamo subito i periodi sinodici
1/Psin,M = 30/7 – 1 = 23/7
1/Psin,V = 21/13 – 1 = 8/13
Psin,M = 7/23
Psin,V = 13/8
Troviamo i nuovi due numeri m e n che ci permettono di stabilire il tempo tra i due allineamenti
m 7/23 = n 13/8
m/n = 13·23/56 = 299/56
299·7/23 = 56·13/8 = 91 anni terrestri
Bel salto temporale… non c’è che dire, ma ancora saremmo ben lontani dall’avere un perfetto allineamento. Bisognerebbe migliorare ancora i rapporti con il periodo terrestre, ma ciò vorrebbe dire numeri m e n sempre più grandi e, di conseguenza, un intervallo tra due allineamenti accurati molto più lungo.
A questo punto, avete già capito cosa si deve fare praticamente.
Si parte da un pianeta e si ottiene il periodo di allineamento t con alti due pianeti (come fatto finora). Si considera questo come il periodo sinodico t di un solo pianeta “ipotetico” e si passa al pianeta reale successivo. Nuovo intervallo t e nuovo periodo sinodico “collettivo”… e così via.
Chi ha voglia di provarci, ci provi pure, ma, anche con le nostre enormi semplificazioni il tempo dovrebbe superare di gran lunga l’età dell’Universo, se si vuole un allineamento quasi perfetto. Se poi entrano in ballo numeri irrazionali, come radice di due, non vi è più nessuna speranza… Ricordiamo che un numero irrazionale non può mai essere espresso come frazione di numeri interi.
Per chi vuole provare, consiglierei di partire da Nettuno e poi aggiungere i pianeti un po’ alla volta arrivando fino a Mercurio (Terra compresa ovviamente). Oppure, partire dalla Terra (P = 1) e poi andare verso l’esterno, limitandosi alle opposizioni (ce n’è già abbastanza).
Tutto ciò si è ottenuto immaginando che esista un punto di partenza in cui vi sia un allineamento perfetto. Se si scegliesse un tempo qualsiasi, bisognerebbe tenere in conto il tempo necessario per avere i vari allineamenti a due a due. La faccenda diventerebbe troppo complicata per descriverla in modo semplice. Ben vengano i calcolatori. Tuttavia, siamo sicuri che, malgrado le nostre semplificazioni, l’ordine di grandezza rimarrebbe invariato.
Nella realtà, poi, entrano in ballo le eccentricità e le inclinazioni, la precessione delle orbite e le varie perturbazioni. Insomma, un lavoraccio anche per i computer più potenti; un gioco che può risolvere (sempre che abbia una soluzione soddisfacente) solo la meccanica celeste più sofisticata.
Non fidatevi , quindi, nemmeno delle risposte che danno i vari Stellarium e giù di lì. Anche loro eseguono semplificazione che alla lunga distruggono qualsiasi risultato. Tanto vale fare qualche calcoletto casalingo, divertirsi ed essere contenti di avere capito il procedimento.
Escludiamo il Sole
Ben diverso è invece il caso dell’allineamento in cui si trascuri la posizione del Sole. La frequenza risulta maggiore e si può scrivere una funzione che illustri il risultato. Ci limitiamo a tre pianeti. Per quattro le cose si complicherebbero un po’ troppo…
Impostiamo nuovamente il problema dell’allineamento.
Due pianeti rivolvono con velocità angolare ω1 e ω2. Ne segue che lo “spazio” percorso, espresso in radianti lungo la circonferenza orbitale, è dato, per un certo istante t qualsiasi, da ω1t e ω2t.
La condizione di allineamento, rispetto al Sole, è allora data semplicemente da:
t(ω1 – ω2) = h 2π
e quindi l’istante t di allineamento è dato da:
t = h 2π/( ω1 – ω2), con h numero intero.
Abbiamo solo detto che si ha allineamento quando la differenza di spazio percorso dai due pianeti è esattamente zero o un multiplo di 2π.
Se consideriamo un terzo pianeta con velocità angolare ω3, si avrà che l’allineamento con ω1 si ottiene per:
t = k 2π/( ω1 – ω3)
Per ottenere l’allineamento dei tre pianeti è, quindi, necessario che i due tempi t siano uguali, ossia:
h/( ω1 – ω2) = k/(ω1 – ω3)
h (ω1 – ω3) = k (ω1 – ω2)
E infine:
(ω1 – ω3)/(ω1 – ω2) = k/h
Dato che k e h sono numeri interi, il loro rapporto è un numero razionale e tale deve essere anche il primo membro.
Se non esistono particolari risonanze, però, le velocità angolari possono essere qualsiasi. Ad esempio, assumiamo che:
ω1 = 2
ω2 = 1
ω3 = 2 - √2
Il rapporto diventa:
(ω1 – ω3)/(ω1 – ω2) = (2 – 2 + √2)/(2 – 1) = √2
Purtroppo questo è un numero irrazionale e non potrà mai essere espresso come rapporto tra numeri interi. La conclusione è che non vi sarà mai un allineamento perfetto! Anche semplificando al massimo la problematica, saremmo sempre schiavi delle velocità angolari dei pianeti, le quali non si curano per niente di stare lontane dai numeri irrazionali…
Come si vede facilmente, un perfetto allineamento non è cosa facile da ottenere, soprattutto se cresce il numero dei pianeti coinvolti. Non vi sarà certo sfuggito che le formule usate poco fa sono del tutto analoghe a quelle che facevano uso dei periodi sinodici. Non abbiamo fatto che ottenere un risultato simile con approcci leggermente diversi, anche se solo apparentemente. Non per altro, la volta scorsa avevamo cercato di approssimare i rapporti dei periodi sinodici con rapporti di numeri interi…
Proviamo adesso a impostare il problema dell’allineamento senza curarci del Sole. E’ proprio il tipo di allineamento più comune, come quello che sta capitando in questi giorni e che è già stato catturato dalla nostra Giorgia. D’altra parte, per avere Marte e Venere vicini (uno è esterno e uno è interno), non possiamo certo avere i pianeti dalla stessa parte, con il Sole esattamente alle spalle! Questo tipo di allineamento si calcola in maniera leggermente più complessa, ma del tutto comprensibile. Limitiamoci al caso di due soli pianeti allineati, ossia visti in congiunzione. La situazione è mostrata in Fig. 4.
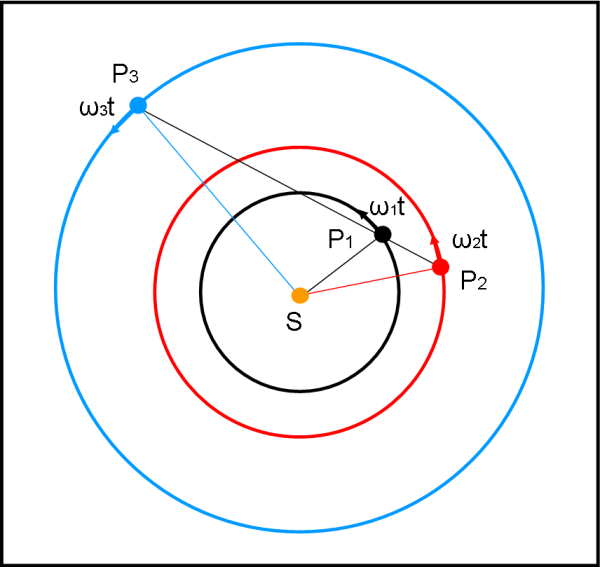
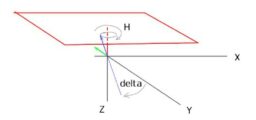
Ricordando il passaggio da coordinate polari a coordinate cartesiane (se avete bisogno di un ripasso andate QUI), un pianeta P, con velocità angolare ω, che è a una distanza r dal Sole (r = raggio della circonferenza orbitale) ha coordinate, istante per istante, date da:
x = r cos (ωt)
y = r sin (ωt)
Applicando le formule ai tre pianeti della figura si ha:
x1 = r1cos(ω1t)
y1 = r1 sin(ω1t)
x2 = r2 cos(ω2t)
y2 = r2 sin(ω2t)
x3 = r3 cos(ω3t)
y3 = r3 sin(ω3t) …. (5)
E’ immediato stabilire che i tre pianeti risultano allineati (come in figura) solo se la pendenza della retta tra P1 e P2 è uguale alla pendenza della retta tra P2 e P3.
Questo fatto può espresso facilmente attraverso le coordinate dei tre punti.
La prima pendenza è data da:
(y2 – y1)/(x2 – x1)
La seconda da:
(y3 – y2)/(x3 – x2)
E, quindi:
(y2 – y1)/(x2 – x1) = (y3 – y2)/(x3 – x2)
Facciamo un po’ di calcoli e scriviamo in altro modo la condizione precedente:
(y2 – y1)(x3 – x2) = (y3 – y2)(x2 – x1)
y2x3 – y2x2 – y1x3 + y1x2 = y3x2 – y3x1 – y2x2 + y2x1
y2x3– y1x3 + y1x2 = y3x2 – y3x1 + y2x1
- y2x3+ y1x3 - y1x2 + y3x2 - y3x1 + y2x1 = 0
(x1y2 – x2y1) + (x2y3 – x3y2) + (x3y1 – y3x1) = 0 …. (6)
Non ci resta, adesso, che sostituire alle x e y le relazioni in funzione dell’angolo e del tempo (ossia le (5))
r1cos(ω1t) r2sin(ω2t) - r1sin(ω1t) r2cos(ω2t) +
+ r2cos(ω2t) r3sin(ω3t) - r2sin(ω2t) r3cos(ω3t) +
+ r3cos(ω3t) r1sin(ω1t) - r3sin(ω3t) r1cos(ω1t) = 0 …. (7)
Per semplificare il tutto bisogna ricordare la formula della sottrazione del seno (si può anche dimostrare, ma per adesso prendiamola per buona), che dice:
sin(a-b) = sin(a) cos(b) – cos(a) sin(b)
Da cui, la (7) diventa:
r1r2 sin ((ω2 - ω1)t) + r2r3 sin ((ω3 - ω2)t) + r1r3 sin ((ω1 - ω3)t) = 0 …. (8)
A questo punto, possiamo eliminare le scomode velocità angolari, dato che, nel caso di orbite circolari, e per una conveniente scelta delle unità di misura, abbiamo (Keplero....):
ω2r3 = 1
Ossia:
ω2 = 1/r3
ω = 1/r3/2
Sostituendo, la (8) diventa:
r1r2 sin((1/r23/2-1/r13/2)t) + r2r3 sin ((1/r33/2-1/r23/2)t) + r1r3 sin ((1/r13/2 -1/r33/2)t) = 0
dividendo tutto per r1r2r3 si ha, infine:
sin((1/r23/2-1/r13/2)t)/r3 + sin((1/r33/2-1/r23/2)t)/r1 + sin((1/r13/2 -1/r33/2)t)/r2 = 0 …. (9)
La parte sinistra della (9), malgrado sembri un guazzabuglio, non è altro che una funzione soltanto di t, dato che i raggi r sono noti. Tutto, quindi, si riduce a trovare gli zeri della funzione, ossia i valori di t per cui essa si annulla. Questi sono proprio gli istanti in cui si ha un allineamento tra i tre pianeti.
Nel caso di Mercurio, Venere e Terra, si ottiene la curva riportata nella Fig. 5, per un intervallo di 5 anni. Attenzione che nelle soluzioni compaiono anche quelle in cui Marte e Venere stanno a 180° rispetto alla Terra (vi è sempre allineamento…).
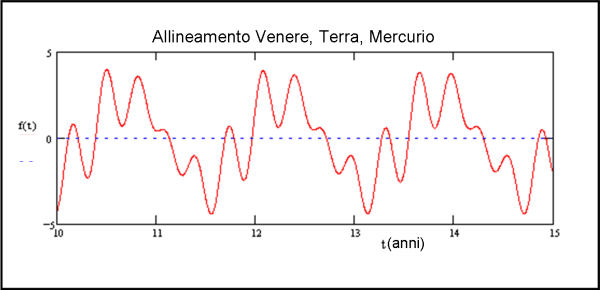
Lo stesso tipo di approccio può essere fatto per altri tre pianeti, ad esempio Venere, Terra e Marte (Fig. 6) e via dicendo.
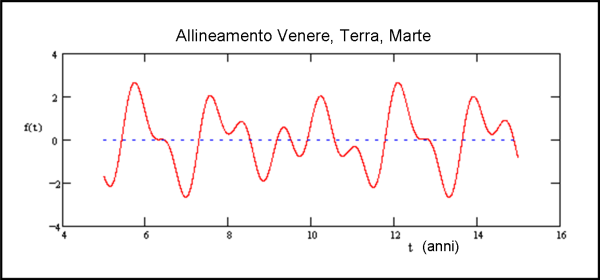
Passare a quattro pianeti implica una complicazione della funzione che non è il caso di discutere.
Posso consigliare, per chi fosse interessato in modo particolare, di leggere questo articolo che sviluppa una teoria per il calcolo di vari tipi di allineamento con un numero di pianeti crescenti e per diverse ampiezze della zona di cielo che li contiene. Ovviamente, sono sempre calcoli basati su semplificazioni orbitali. Tuttavia, come si può notare, un allineamento totale e abbastanza stretto supera di gran lunga l’età del Sistema Solare.
A questo punto, sapendo di cosa stiamo parlando e delle difficoltà relative all’approssimazione usata per descrivere il sistema planetario, chi vuole può anche utilizzare Stellarium o cose del genere, tenendo comunque conto che anche questi programmi si basano su calcoli e approssimazioni che, per tempi molto lunghi, possono dare risultati completamente privi di senso.
QUI le immagini di un raro allineamento planetario vissuto in diretta