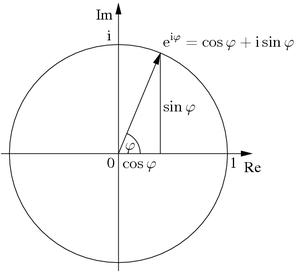
Il gioco è quasi terminato e possiamo tornare, lentamente, verso una visione più seria e precisa. Ciò che abbiamo ottenuto, divertendoci, non è altro che una formula di importanza fondamentale.
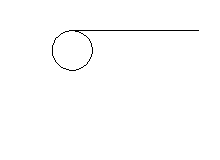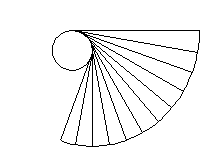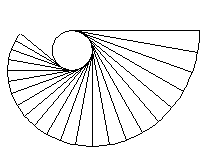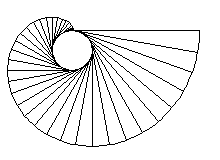
Gli sviluppi in serie di seno e coseno derivano dall'applicazione della formula di Taylor. Tuttavia, vi è un modo puramente geometrico per ottenere lo stesso risultato.
Diamo una rapida soluzione agli esercizi proposti nel capitolo precedente (39), proponendo lo sviluppo in serie e descrivendo la formula più compatta. Un bravo ai nostri (due) lettori che si sono cimentati. Bando alle ciance, è ora di buttarsi all’interno del mondo degli integrali.
In questo articolo applichiamo la serie di Mclaurin a due funzioni estremamente importanti. Di seguito trovate anche qualche esercizio…
Concludiamo la costruzione della serie di Taylor, introducendo il suo termine generale. L'ho letta e riletta, ma non garantisco che non vi sia ancora qualche refuso. Picchiate duro e non abbiate pietà di me!!
Questo non è un articolo facile, non tanto per i concetti che esprime, ma piuttosto per il numero di passaggi che siamo obbligati a fare. Si basa su un teorema classico delle funzioni e presenta perciò un metodo rigoroso, che abbisogna, però, di iterazioni successive (mai facili da digerire e da tenere sottocchio). Mi sembrava, però, doveroso proporlo.
Anche se abbiamo concluso (almeno momentaneamente) lo studio delle funzioni, queste ultime rimangono un punto fondamentale della matematica e continuano a essere nel nostro mirino. Vogliamo arrivare al calcolo dei loro integrali e quindi cominciamo con il loro sviluppo in serie, un argomento poco divulgato che è però di importanza fondamentale.

Dopo la dimostrazione dell'irrazionalità di π ecco quella del numero di Nepero. La dimostrazione è la più semplice che ho trovato, e si basa sostanzialmente sugli sviluppi in serie di Taylor con resto di Lagrange.

Un problema che ha assillato i più grandi matematici dell'epoca, che, come sempre o quasi, è stato risolto genialmente da Eulero. Seguiamo il suo ragionamento...
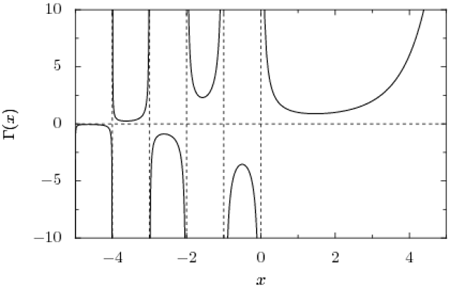
Cerchiamo di accogliere (e seguire) con grande interesse l'entrata in ballo di una nuova funzione che riesce a compiere un vero e proprio miracolo. E lo fa, anche, in modo estremamente comprensibile. Non spaventatevi per la presenza di integrali... tutto è più semplice (almeno concettualmente) di quanto sembri! Io ce la metterò tutta per cercare di fare apprezzare da tanti un vero tesoro matematico. L'appendice 2 è dedicata ai più esperti, amanti degli integrali, ma non è necessaria.
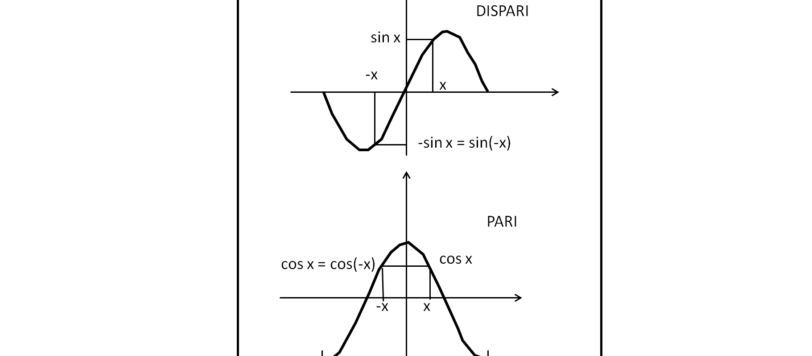
Iniziamo la nostra analisi di Fourier. La trattazione sarà abbastanza faticosa ed è facile che, pur leggendo e rileggendo, nelle formule siano rimasti errori, mancanza o sovrappiù di parentesi e cose del genere. Mi raccomando, evidenziate i vari errori nei commenti in modo da sistemare la faccenda. Teniamo anche conto che non ho potuto usare il latex (che si perde nel tempo) e, quindi, la scrittura delle formule sono state veramente un lavoro difficile. Buona lettura...

Beh... a scanso di equivoci vi dico subito che il seno in questione è la ben nota funzione trigonometrica e che gli "indiani" sono proprio gli abitanti dell'India.
Cari amici e collaboratori del circolo. Sì siete tutti collaboratori perché con le vostre domande e dubbi collaborate a renderlo il più completo possibile. Parlare di completezza è assurdo, dato che ogni argomento è pronto a stimolarne almeno altri dieci e via dicendo. Non potremo certo fare tutto, ma, almeno dobbiamo provare a formare le basi fondamentali della fisica e, di conseguenza, dell’astrofisica, a costo di trascurare quasi del tutto le illazioni più o meno plausibili della ricerca più “moderna”. Una scelta di questo circolo, che penso accontenti la maggior parte di chi lo segue con costanza. Veniamo al dunque… abbiamo fatto 1000! Sì, 1000 articoli pubblicati su questo circolo. Un bel traguardo, non c’è che dire. Sarà difficile raddoppiare (almeno da parte mia), però… chissà… Approfittiamo di questo risultato per fare un po’ di statistica spiccia.

un numero con infinite cifre decimali sembrerebbe tutto fuorché qualcosa di estremamente naturale. Eppure proprio questo numero regola i processi naturali fondamentali.

Non accadeva da 18 anni e dovremo attenderne altrettanti per poter di nuovo ammirare uno spettacolo del genere... se qualcuno tra voi lettori è riuscito a scattare una bella foto e ha piacere di inviarcela, può farlo scrivendo una mail a infinitoteatrocosmo@gmail.com. Vincerà un bel... niente (tanto per cambiare), ma avrà la soddisfazione di consegnare alla memoria dei posteri la sua foto, che verrà pubblicata nel blog più infinito dell'Universo conosciuto.
Nel frattempo entriamo dietro le quinte dello spettacolo per carpirne i più intimi segreti!
- 1
- 2