(QI) Qual è la relazione corretta ? **

22/09/22

(QI) Qual è la relazione corretta ? **

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:9

Vi pongo un semplice problema matematico...

Consideriamo un numero decimale periodico, ad esempio 0.999999999....

Quale di queste due relazioni è vera?

0.9999 ... = 1

0.9999 ... < 1

Oppure sono vere entrambe o nessuna delle due ?

Voglio anche la dimostrazione rigorosa della vostra risposta.

Un quiz facile prima di tornare a cose più impegnative... ma non andate a cercare in rete (altrimenti che gusto c'è?)

QUI la soluzione

Articoli correlati

9 commenti

  1. maurizio rovati
    22/09/2022 at 19:22

    Penso sia vera la prima, 0,999...=1 perchè:

    essendo (1/3)=0,333... allora si può dire che

    (1/3)= (1/3) e quindi 3*(1/3)=1

  2. Fabrizio
    22/09/2022 at 22:37

    Sono per 0.9999...=1.

    Oltre a quelle di coerenza del calcolo algebrico, come quella indicata da Maurizio,

    una ragione potrebbe essere che non riesco a trovare un numero, per quante cifre decimali possa metterci, che si intreponga tra 0.9999... e 1. Quindi i due numeri coincidono.

  3. Andy
    23/09/2022 at 00:31

    Io ho fatto questo tipo di ragionamento, partendo da "lontano"; considero inizialmente 1 sola cifra decimale

    0,9 =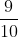 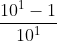\frac{9}{10} = \frac{10^1-1}{10^1} < 1 ; continuo con 2 cifre decimali: 0,99 = 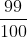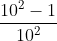\frac{99}{100} = \frac{10^2-1}{10^2} < 1

    con 3:    0,999 =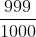 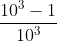\frac{999}{1000} = \frac{10^3-1}{10^3} < 1

    con 4:    0,9999 =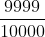 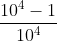\frac{9999}{10000} = \frac{10^4-1}{10^4} < 1

    con 5:    0,99999 =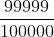 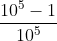\frac{99999}{100000} = \frac{10^5-1}{10^5} < 1

    .....

    con n cifre decimali: 0,99999999999999....... =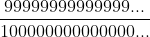 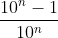\frac{99999999999999...}{100000000000000...} = \frac{10^n-1}{10^n} < 1

    e questo con n numero finito.

    Ma se n tende all'infinito, devo ricorrere ai limiti:

    \lim_{n \to \infty}{\frac{10^n-1}{10^n}} = \lim_{n \to \infty}{(1-\frac{1}{10^n})} = 1

  4. Vincenzo Zappalà
    23/09/2022 at 07:22

    Come immaginavo... guai a scendere di livello :wink: .

  5. maurizio rovati
    06/10/2022 at 14:41

    Però anche:  0,111... = 1 :roll: 

  6. Vincenzo Zappalà
    06/10/2022 at 14:54

    sembrerebbe di no... puoi dimostrarlo?

  7. maurizio rovati
    06/10/2022 at 15:11

    Certamente... ma lascio ancora un po' di tempo a tutti :idea:

  8. Vincenzo Zappalà
    06/10/2022 at 15:25

    Beh... tutto è possibile se si cambia base... Per quella decimale non è vero, però.

  9. maurizio rovati
    06/10/2022 at 16:13

    Infatti! Un mio amico programmatore mi diceva che esistono solo 10 tipi di persone: quelli che capiscono e quelli che non capiscono... :wink: 

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.