Categorie: Matematica
Tags: carrozzeria automobili computer grafica curve di Bezier interpolazione
Scritto da: Vincenzo Zappalà
Commenti:4
Come scegliere la curva più "bella" ***
Sappiamo che vi sono vari metodi per tracciare una curva che approssimi al meglio una serie di punti osservati. Esiste sempre un polinomio di un certo grado che permetta di avvicinarsi sempre più allo scopo, il cui grado dipende ovviamente dal numero di punti in nostro possesso.
Stiamo, ovviamente, parlando di interpolazione.
Tuttavia, grazie alla ricerca di armonia nelle linee delle carrozzerie delle automobili, intorno agli anni '60 del secolo scorso, sono stati sviluppati algoritmi capaci di mostrare facilmente (grazie ai computer) soluzioni sempre diverse per curve passanti per due punti prefissati. Minimi cambiamenti in certi punti "di controllo" hanno permesso di poter tracciare una serie infinita di curve passanti per quei punti, perfettamente smussate, armoniose e, ovviamente, rispondenti ai parametri fisici attivi durante il movimento dell'automobile. Il merito dell'applicazione alle carrozzerie delle automobili si deve all'ingegnere francese Pierre Bezier, da cui il nome di curve di Bezier. In generale, questo tipo di approccio è utilizzato in tutti i campi della "computer grafica", ma noi ci limiteremo al concetto base.
Il procedimento non è molto diverso da quello utilizzato per l'interpolazione, ma invece di cercare di passare per punti prefissati, la curva di Bezier impone soltanto un punto di partenza e un punto di arrivo, permettendo la visualizzazione e la scelta della curva più bella e utile che inizi e termini in quei due punti.
Cominciamo con la curva di grado più basso, ossia quella rettilinea tra i due punti P0e P1. Vogliamo descrivere un generico punto P (lo chiamiamo P'0) che stia sul segmento P0P1, la cui posizione vari linearmente con un certo parametro t che va da 0 a 1. .
La migliore rappresentazione della situazione è quella vettoriale, mostrata in Fig. 1.

Dati i punti P0 e P1 prolunghiamo la loro congiungente e consideriamo un punto O qualsiasi come origine. Questo ci permette di definire due vettori: OP0 e OP1, che possiamo chiamare P0 e P1.
Vogliamo legare un qualsiasi punto Po', compreso tra P0 e P1, ai vettori P0 e P1 e al parametro t.
Definiamo, allora, il vettore OP0' = P0'(t)
E' immediato concludere che tale vettore è la somma di due vettori: P0 e P1 - P0 moltiplicato per il parametro t:
P0'(t) = P0 + (P1 - P0)t .... (1)
Se t = 0, esso coincide con P0, mentre, se t = 1, coincide con P1.
Anche se non lo esplicitiamo più, P0' è funzione di t.
Volendo, la forma vettoriale può essere trasformata facilmente nelle sue componenti lungo gli assi cartesiani.
La (1) può essere scritta in modo più utile per una sua generalizzazione:
P0' = P0(1 - t) + P1 t ... (2)
D'ora in poi non scriveremo più il simbolo vettoriale, sapendo ormai il suo significato. La (2) ci permette di descrivere ogni punto tra P0 e P1 in funzione del parametro t, attraverso una relazione lineare.
Passiamo adesso a una curva di secondo grado. Per far ciò introduciamo un terzo punto P2. Lo scopo è quello di costruire curve di secondo grado che partano da P0 e arrivino in P2, tenendo però in conto il punto P1 che assume il ruolo di "controllore" della curva. Utilizziamo la Fig. 2.
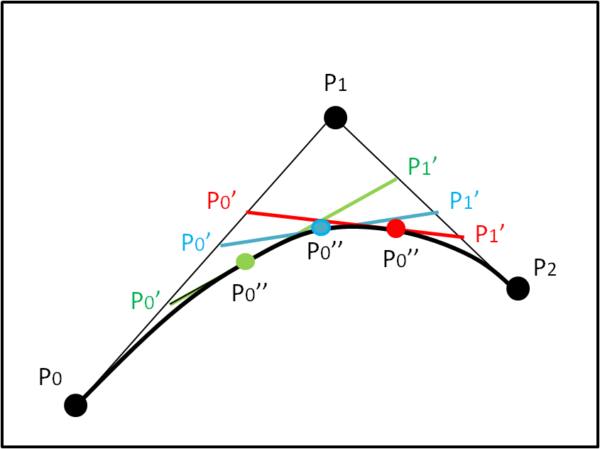
Congiungiamo P0 a P1 e P1 a P2. Definiamo, poi, i punti P0' e P1', seguendo le regole del caso precedente. In altre parole, facciamo variare il parametro t in modo che nell'intervallo 0-1 sia descritto sia il segmento PoP1 che P1P2. Tra Po e P1 troviamo il punto P0', mentre, tra P1 e P2 troviamo il punto P'1. Uniamo questi due punti (segmenti colorati) e ci ritroviamo ancora nel caso di Fig. 1. Al variare di t, varia il segmento Po'P1', ma per ogni suo valore è possibile trovare il punto P0" tale che soddisfi la relazione (2) tra P0' e P1'. Nella figura sono stati inseriti solo tre valori del segmento Po'P1', ma è ovvio che se ne possano disegnarne n a piacere (cosa che il calcolatore sa fare egregiamente).
Vediamo come si trasforma la relazione (2)
Essa vale, per Po e P1
P0' = P0(1 - t) + P1 t .... (3)
Mentre per P1 e P2 vale
P1' = P1(1 - t) + P2 t .... (4)
Applicando la (2) ai vari segmenti P0' P1' otteniamo i punti P0", tra ogni punto Po' e P1', al variare di t:
P0" = P0'(1 - t) + P1' t .... (5)
Sostituendo i valori di P0 e P'1 della (3) e (4) nella (5), abbiamo:
P0" = (P0(1 - t) + P1 t)(1 - t) + (P1(1 - t) + P2 t) t
P0" = P0(1 - t)2 + 2P1 t (1 - t) + P2 t2 .... (6)
che è la nostra curva di secondo grado. Essa passa per P0 e P2, ma non per P1, che fa solo da "controllore".
La faccenda si ripete se aggiungiamo un quarto punto P3. Per i primi 3 punti rifacciamo quanto fatto nel caso precedente, come mostra la Fig. 3.
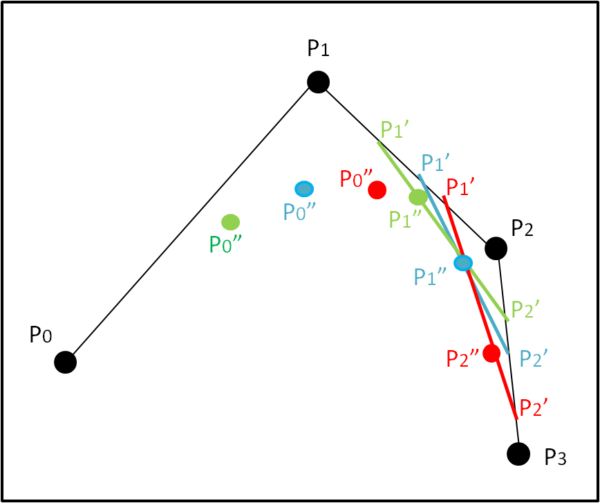
Poi ripetiamo l'operazione per i 3 punti P1, P2 e P3 , ottenendo:
P1" = P1(1 - t)2 + 2P2 t (1 - t) + P3 t2 .... (7)
A questo punto eseguiamo la (2) per i segmenti che congiungono P0" e P1"(Fig. 4)
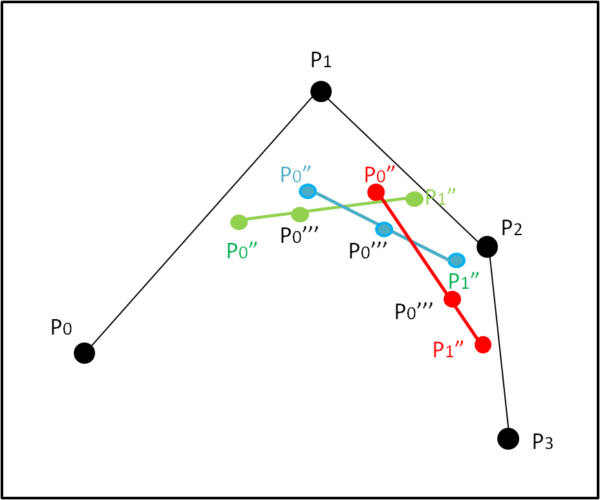
P0"'(t) = P0"(1 - t) + P1" t .... (8)
E andiamo a sostituire la (6) e la (7) nella (8)
P0"' = (P0(1 - t)2 + 2P1 t (1 - t) + P2 t2)(1 - t) + (P1(1 - t)2 + 2P2 t (1 - t) + P3 t2) t
P0"' = Po(1 - t)3 + 2 P1 t(1 - t)2 + P2 t2(1 - t) + P1 t (1 - t)2 + 2 P2t2 (1 - t) + P3 t3
P0"' = Po(1 - t)3 + 3 P1 t(1 - t)2 + 3P2 t2(1 - t) + P3 t3 .... (10)
Che è una cubica (Fig. 5)

Ovviamente, si può continuare per un numero di punti grandi a piacere. Ciò che non cambia è il fatto che la curva passa sempre per il primo e per l'ultimo, mentre tutti quelli intermedi fanno da "controllori".
La forma generalizzata per un numero n + 1 di punti (da P0 a Pn), vale:
P0n (t) = ∑nk = 0
Ricordiamo che 
Una relazione facilmente inseribile come "comando" in un computer, scegliendo i punti P0, ..., Pn. In realtà, almeno per quanto riguarda la progettazione delle carrozzerie delle automobili, si fissano i punti iniziale e finale e poi lavorando su quelli intermedi si fa variare la curva fino a ottenere il risultato più accattivante. La Fig. 6 ci mostra un esempio nel caso di soli 3 punti.
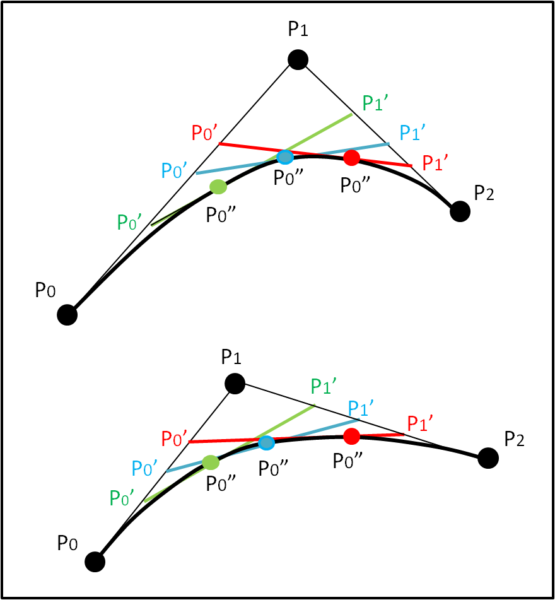



4 commenti
Da anni utilizzo le curve di Brezier nei miei vari programmi Adobe di grafica senza avere mai saputo nulla della loro base teorica. Grazie. Però ora qualche dubbio mi resta, ad esempio direi che in questo disegno ci sono 3 punti fissi e 4 controllori, ma probabilmente non è così semplice come me l'immagino io
Quello che penso è che si applica due volte la curva di Bezier... ma è un disegno poco indicativo
Ho provato a verificare l'ipotesi di Enzo su due applicazione di grafica che mi capita di utilizzare: GIMP e Blender.
Effettivamente entrambe le app realizzano le curve giustapponendo curve di Bézier del 3° grado. Questa giustapposizione di curve è facilitata dal fatto che è semplice ottenere curve "lisce" che hanno la stessa tangente nei punti comuni. Infatti le tangenti sono fissate dai vettori tra l'estremo ed il punto di controllo più vicino (es.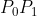 ). Infatti facendo la derivata rispetto a t della funzione (11) e calcolandola in t=0 ottengo:
). Infatti facendo la derivata rispetto a t della funzione (11) e calcolandola in t=0 ottengo:
L'ultimo termine e tutti i seguenti (che non ho riportato) si annullano in t=0 poiché contengono il fattore t, quindi:
Forse è questo il vantaggio delle curve di Bézier. Per ottenere curve "lisce" basta giustapporre curve che hanno il punto estremo comune ed i punti di controllo adiacenti allineati.
Qui due esempi di due curve di Bézier giustapposte "lisce" ottenute ruotando l'allineamento dei punti di controllo adiacenti al punto intermedio comune. Nella figure appaiono anche i punti di controllo.
Se non c'è l'allineamento si possono ottenere curve con punte come questa.
Ottimo approfondimento Fabry. Grazie!
Le curve di Bezier portano a soluzioni veramente disparate... ci sarebbe da scrivere interi libri... Accontentiamoci del concetto base.