Due cerchi incatenati **/***

15/01/21

Due cerchi incatenati **/***

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:30

E' un periodo che sforno tanti quiz e sono contento di vedere che riscuotono successo. Anzi, mi accorgo che, a volte uno a volte un altro, siete prontissimi a rispondere. Voglio provare a divertirmi anch'io, sicuro della vostra partecipazione!

Prendendo spunto da un quiz geometrico presentato nelle bellissime tavolette giapponesi (Sangaku), ho cercato di generalizzare la situazione e mi sono messo a cercare la soluzione. A quel punto mi sono detto: "Perché non chiedere aiuto ai miei amici-colleghi del Circolo?". Ragione per cui, pur avendo trovato una soluzione, sono sicuro che sia migliorabile in termini di compattezza e semplicità. Sospendo lo studio e lascio a voi il compito di aiutarmi.

Il problema è piuttosto semplice nella sua descrizione.

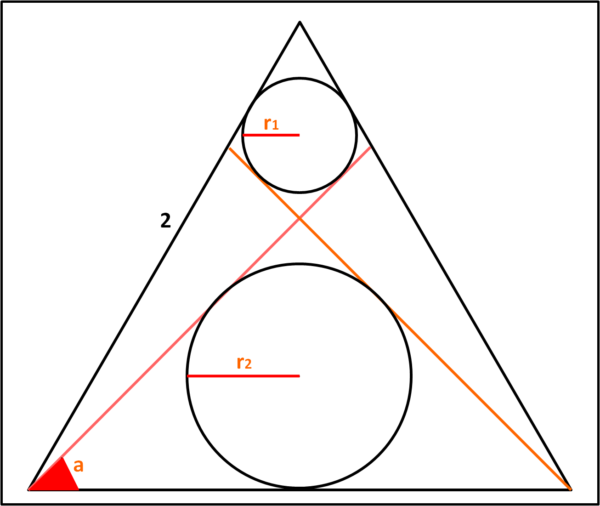
Consideriamo un triangolo equilatero di lato uguale a 2. Da due dei suoi vertici (ad esempio, quelli in basso nella figura che segue) tracciamo due rette ugualmente inclinate di un angolo a rispetto all'asse orizzontale. E' facile individuare due cerchi che siano tangenti alle rette e ai lati del triangolo.

Il problema originale è:

Quanto vale il raggio dei due cerchi quando essi sono uguali? Ossia quanto vale r1 = r2?

Io, però, ho cercato di generalizzare il problema e trovare i valori dei raggi in funzione dell'angolo a e, quindi, determinare r1=r2 come caso particolare.

In effetti, la soluzione del problema originale delle tavolette giapponesi chiedeva solo di determinare il caso particolare che non aveva bisogno della generalizzazione. Vale la pena, comunque, risolverlo.

Come vi dicevo, la soluzione da me trovata è sicuramente corretta, ma non mi piace tanto "esteticamente". Invece di pensarci ancora sopra (ma, forse, un po' lo farò) "scarico" il problema su di voi, sicuro che troverete la soluzione più "elegante", tanto per cambiare!

Direi che è un esercizio da due asterischi o forse tre... me lo dimostrerete voi...

 

QUI la prima parte della soluzione, QUI la seconda e (forse) un nuovo teorema... QUI la dimostrazione del nuovo "Teorema di Zappalà"!

 

Articoli correlati

30 commenti

  1. Giovanni
    16/01/2021 at 10:14

    Buongiorno.

    Credo di aver risolto il problemino, ma non so come si fa ad allegare un disegno (come quello di Vincenzo, ma con lettere, angoli, bisettrici, ecc.)

    Stasera, al mio rientro, vedrò cosa posso fare...

    Saluti a tutti.

     

  2. Vincenzo Zappalà
    16/01/2021 at 10:49

    caro Giovanni,

    puoi sempre inviarlo a Daniela (Scherzy) e lei è bravissima a inserirla nei commenti...

    Anche se dicevo di non farlo, ho trovato anch'io una nuova formula, ma spero che tu abbia fatto ancora meglio... :wink:

  3. Daniela
    16/01/2021 at 11:53

    Ciao Giovanni,

    per inserire un'immagine in un commento, la si deve caricare su uno di quei siti ad hoc per questo tipo di servizio (per esempio questo https://imgur.com/ ma ce ne sono molti altri), dopodiché copiare il link che corrisponde all'immagine ed incollarlo nel campo "sorgente" del riquadro "inserisci/modifica immagine" (il secondo da destra nella barra degli strumenti dei commenti, accanto a fx).

    Questa è la "strada maestra" per la pubblicazione di immagini, ma per la soluzione di questo quiz, inviami pure la tua immagine a infinitoteatrocosmo@gmail.com e ci penso io.

     

  4. Arturo Lorenzo
    16/01/2021 at 19:24

    Faccio riferimento alla seguente figura:

    Ho, quindi, chiamato con x l'angolo indicato con a nella figura del quiz. Intanto è immediatamente (triangolo rettangolo AHO1:

    r_{1}=1*tan(\frac{x}{2})=tan(\frac{x}{2})                (1)

    Poi , se considero il triangolo rettangolo che ha per ipotenusa il segmento O1K, risulta:

    r_{1}=\overline{O_{1}K}sen(90-x)=\overline{O_{1}K}cos(x)

    da cui:

    \overline{O_{1}K}=\frac{r_{1}}{cos(x)}

    Ancora, dal triangolo rettangolo che ha per ipotenusa il segmento KO2, risulta:

    r_{2}=\overline{O_{2}K}sen(90-x)=\overline{O_{2}K}cos(x)

    da cui:

    \overline{O_{2}K}=\frac{r_{2}}{cos(x)}

    E, infine, dal triangolo rettangolo che ha per ipotenusa il segmento O2C, risulta:

    r_{2}=\overline{O_{2}C}sen30=\frac{\overline{O_{2}C}}{2}

    da cui:

    \overline{O_{2}C}=2r_{2}

    L'altezza HC del triangolo equilatero è pari a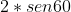 2*sen60  cioè  \sqrt{3}.

    Ma è anche:

    HC=r_{1}+O_{1}K+KO_{2}+O_{2}C

    Sostituendo le espressioni prima ricavate ottengo:

    r_{1}+\frac{r_{1}}{cos(x)}+\frac{r_{2}}{cos(x)}+2r_{2}=\sqrt{3}

    che posso scrivere come:

    r_{1}(1+\frac{1}{cos(x)})+r_{2}(2+\frac{1}{cosx})=\sqrt{3}               (2)

    Mettendo a sistema la (1) e la (2) trovo, dopo alcuni passaggi:

    r_{2}=\frac{\sqrt{3}-tan(\frac{x}{2})(1+\frac{1}{cos(x)})}{2+\frac{1}{cos(x)}}                 (3)

    Ho, a questo punto, entrambe le espressioni di r1 ed r2 in funzione dell'angolo x.

    Per trovare l'angolo x in corrispondenza del quale i due raggi sono uguali, basta eguagliare la (1) con la (3). Alla fine ottengo x=35,264° , cui corrisponde una lunghezza dei raggi r1 = r2 = 0,318 (circa).

     

     

  5. Vincenzo Zappalà
    17/01/2021 at 07:11

    aspettiamo anche Giovanni... :wink:

  6. Giovanni
    17/01/2021 at 08:07

    Buongiorno.

    Scusate, ma ieri sera siamo rientrati tardi.

    Ho inviato il mio disegno a Daniela, ma nel frattempo si può capire ciò che voglio dire, anche utilizzando il disegno di Arturo Lorenzo, a cui va anche il mio apprezzamento per la soluzione.

    Ho risolto il problema in modo un po' diverso da Arturo Lorenzo, ma il risultato è lo stesso.

    (Inoltre, devo imparare anche a usare la tastiera matematica e i disegni geometrici. Forse, nella prossima ... vita!)

    Grazie a Daniela, se riesce a inserire il mio disegno, fatto a mano...

    Saluti a tutti.

     

     

  7. Giovanni
    17/01/2021 at 08:08

    Soluzione.

    Il triangolo ABC è un triangolo equilatero con i lati uguali a 2 e gli angoli di 60°.

    1. Consideriamo il triangolo rettangolo A-D-O2.

    R2 = 1 x tang α/2

    2. Consideriamo il triangolo rettangolo A-O1-K.

    R1 = i x sen β = i x sen [(60-α)/2]

    L'ipotenusa i si può calcolare considerando il triangolo A-D-O1, anch'esso rettangolo.

    i = 1/sen ω dove : ω = (90 - α - β) = (90 - α - [(60-α)/2] = (60 - α/2)

    i = 1/sen (60-α/2)

    da cui : R1 = 1/sen (60-α/2) x sen [(60-α)/2]

    Per cui si possono calcolare R1 e R2 al variare di α.

    3. Calcolo del valore di α quando i due cerchi sono uguali.

    R1 = R2

    1/sen (60-α/2) x sen [(60-α)/2] = 1 x tang α/2

    Risolvendo l'equazione trigonometrica, si può trovare α.

  8. Vincenzo Zappalà
    17/01/2021 at 08:25

    Ed ecco il nostro Giovanni arrivare puntuale!

    Mentre aspettiamo ancora un poco... volevo far presente una cosa importante (PER TUTTI)

    Manca ancora la soluzione utilizzata nella tavoletta giapponese, ossia quella in cui si determina il valore di R1 = R2 direttamente e NON come caso particolare della problematica più generale che ho cercato di sviluppare con il vostro aiuto.

    Un metodo molto carino che dà un risultato a dir poco interessante... FORZA!!

  9. Daniela
    17/01/2021 at 08:37

    Ecco il triangolo di Giovanni:

    Il triangolo ABC è un triangolo equilatero con i lati uguali a 2 e gli angoli di 60°.

    1. Consideriamo il triangolo rettangolo A-D-O2.

    R2 = 1 x tang α/2

    2. Consideriamo il triangolo rettangolo A-O1-K.

    R1 = i x sen β = i x sen [(60-α)/2]

    L'ipotenusa i si può calcolare considerando il triangolo A-D-O1, anch'esso rettangolo.

    i = 1/sen ω dove : ω = (90 - α - β) = (90 - α - [(60-α)/2] = (60 - α/2)

    i = 1/sen (60-α/2)

    da cui : R1 = 1/sen (60-α/2) x sen [(60-α)/2]

    Per cui si possono calcolare R1 e R2 al variare di α.

    3. Calcolo del valore di α quando i due cerchi sono uguali.

    R1 = R2

    1/sen (60-α/2) x sen [(60-α)/2] = 1 x tang α/2

    Risolvendo l'equazione trigonometrica, si può trovare α.

  10. leandro
    17/01/2021 at 12:39

    Ribaltando il triangolo equilatero secondo la retta orizzontale passante per il punto K
    si ottengono due triangoli che si intersecano.
    I due cerchi, essendo identici ed essendo k equidistante dai centri( perché sottende lo sesso arco), devono sovrapporsi.

    Le distanze dei 2 centri dal punto K devono quindi essere uguali, ed essendo uguali i raggi,
    il punto K deve essere equidistante dal vertice del triangolo e la sua base.
    Poiché l'altezza del triangolo è \sqrt{3}, tale distanza deve essere \sqrt{3}/2 e
    tale deve essere la tangente dell'angolo incognito.

  11. Giovanni
    17/01/2021 at 12:49

    Non ho fatto il disegno, perciò mi sbilancio con il rischio di prendere una cantonata...

    I raggi dei due cerchi sono uguali quando è uguale la distanza tra i piedi delle perpendicolari alle semirette che formano un angolo ∝ con la base del triangolo ABC.

    Vincenzo (dopo pranzo, perché sarà più benevolo...) mi dirà se ho ragione.

    Grazie e buona domenica.

     

  12. Vincenzo Zappalà
    17/01/2021 at 14:59

    caro Leandro,

    non so se ho capito bene... ma a me non risulta che KC sia uguale a KH (nella figura di Arturo)...

    Comunque sia, la tangente non è uguale a √3/2, ossia l'angolo NON è uguale a 41° circa.

  13. Vincenzo Zappalà
    17/01/2021 at 15:06

    caro Giovanni,

    Tu dici:

    " la distanza tra i piedi delle perpendicolari alle semirette che formano un angolo ∝ con la base del triangolo ABC."

    scusami, ma non capisco proprio a che distanza ti riferisci. "Perpendicolari" tracciate da dove?

  14. Vincenzo Zappalà
    17/01/2021 at 16:11

    cari ragazzi,

    a parte la determinazione dell'angolo a che ci permette di calcolare i due raggi (quello che hanno provato a fare Arturo e Giovanni) rimane il problema "giapponese", ossia:

    DETERMINARE r1 = r2 SENZA DOVER RICAVARE l'angolo a. Questo si ricava in un secondo tempo, conoscendo r... dato che tan(a/2)= r

    Ricordiamoci che la domanda del quiz era:

    Quanto vale il raggio dei due cerchi quando essi sono uguali? 

    Perché mai dovremmo ricavare prima a se se ne può fare a meno?

  15. Vincenzo Zappalà
    17/01/2021 at 16:13

    Caro Artù, unisciti pure a Leandro e Giovanni... non hai ancora finito! :-P

  16. Giovanni
    17/01/2021 at 16:15

    Caro Vincenzo, lo so che ci vuole un disegno, ma conosci le mie difficoltà.

    Comunque, nel bel disegno di Arturo ci sono già due raggi : sono perpendicolari alla retta che delimita  l'angolo ∝ e che passa per A e K.

    Disegniamo gli altri due raggi perpendicolari alla retta KB.

    Si formano due quadrilateri, diversi in grandezza, ma con gli angoli uguali.

    Nel disegno di Arturo è necessario diminuire l'angolo alfa (x, nella figura), affinché i due cerchi diventino uguali.

    A questo punto, i due quadrilateri avranno gli angoli sempre uguali, ma anche i lati saranno uguali.

    La distanza orizzontale (o se vuoi, le corde dei due cerchi) passanti per l'incrocio tra i raggi e le rette AK e KB, saranno uguali fra loro.

    Nella prima parte, mi pare che anche il ragionamento di Leandro è corretto.

    Se poi Arturo volesse aggiungere gli altri due raggi e le lettere, il mio discorso apparirà più chiaro a tutti.

    Grazie.

  17. Vincenzo Zappalà
    17/01/2021 at 17:17

    grazie a te Giovanni... adesso ci studio sopra...

  18. Vincenzo Zappalà
    17/01/2021 at 17:34

    caro Giovanni,

    va benissimo riferirci alla figura di Arturo...

    Sì, sì, sono d'accordo... è cosa immediata a dimostrarsi, ma cosa c'entra con la conclusione di Leandro:

    "il punto K deve essere equidistante dal vertice del triangolo e la sua base." ?

    A me viene ben diverso e, comunque, r rimane funzione dell'angolo a. E come faccio a trovare sia r che a?

    E poi il problema è calcolare r senza calcolare l'angolo a...

    Oppure, semplificare le formule che danno r e R in funzione di a.

    Sono due problemi diversi...

  19. leandro
    17/01/2021 at 18:59

    mi correggo: la retta orizzantale di ribaltamento  è a 1/3 dell'altezza, cioè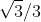 \sqrt{3}/3 , è una stella di David di lato 2/3.

  20. Vincenzo Zappalà
    17/01/2021 at 19:05

    Mi dispiace Leandro, ma la tangente di a non è nemmeno √3/3 = 0.5774. Verrebbe un angolo a di 30°, il che non è...

  21. leandro
    17/01/2021 at 20:06

    Peccato, la figura era proprio bella. Il raggio sarebbe venuto = \sqrt{3}/6

  22. Vincenzo Zappalà
    18/01/2021 at 05:41

    eh sì, sarebbe stato bello, ma... :(

  23. Vincenzo Zappalà
    18/01/2021 at 06:10

    Direi che è meglio fare il punto della situazione:

    (1) Sono state trovate un paio di relazioni che legano i raggi angolo e soltanto con l'angolo a e(ovviamente) anche al triangolo equilatero. Esse permettono di far variare a e determinare i due raggi. QUI CI STAREBBE BENE UNA ANIMAZIONE.

    (2) Quelle due relazioni, poste una uguale all'altra permettono di avere un'equazione in funzione della sola a, la cui soluzione, però, si determina solo per via grafica. LA MIA SPERANZA ERA DI TROVARE UNA SOLUZIONE PURAMENTE ALGEBRICA SENZA FAR RICORSO AI PROGRAMMI DI RETE.

    (3) In realtà, per il caso r1 = r2, si può trovare una relazione alquanto semplificata (SCRIVETELA) che comunque ha ancora al suo interno sia r=r1=r2 che l'angolo a. Anche qui si può fare il grafico e trovare il suo zero, ma...

    (4) Vi è poi il problema iniziale, della vera tavoletta giapponese, che è particolarmente intrigante:

    DETERMINARE IL VALORE DI r SENZA AVER BISOGNO DELL'ANGOLO a.

    (5) Risolta la (4) mi chiedevo se era possibile legare in qualche modo i risultati ottenuti.

  24. Vincenzo Zappalà
    19/01/2021 at 07:49

    caro Giovanni,

    ho riguardato la tua soluzione, mentre stavo preparando la risposta, e ho notato che c'è qualcosa che sicuramente non va...

    Tu trovi:

    R1 = 1/sen (60-α/2) x sen [(60-α)/2]

    Ma è una relazione che non ha senso, sia se il secondo seno fosse al numeratore o al denominatore.

    Nel primo caso, otterresti R1 = 1 (assurdo)

    Nel secondo caso

    R1 = 5.71   ancora peggio...

    Non ho controllato passaggio per passaggio ma c'è qualcosa che non va...

  25. Giovanni
    19/01/2021 at 16:57

    Caro Vincenzo.

    Secondo me il problema sta nella grafia che ho usato (la tastiera...), che non c'entra niente con la matematica.

    Per chiarire : il primo seno sta al denominatore, il secondo al numeratore.

    Gli esempi che avevo fatto (per essere sicuro dei calcoli) erano tutti corretti. Di solito riesco a scambiare (ogni volta che faccio un'equazione) il segno + con il segno -

    I risultati (R1 = R2) coincidono con quelli di Arturo.

     

    Pe quanto riguarda l'ultimo quesito, anch'io mi ero chiesto se, a quell'epoca, i giapponesi conoscessero le funzioni trigonometriche.

    Ho provato varie soluzioni, ma nessuna mi porta al risultato.

    Poiché anche gli altri tacciono, ce la racconti la soluzione ?

    Grazie e cordiali saluti.

     

     

     

     

  26. Vincenzo Zappalà
    19/01/2021 at 17:18

    caro Giovanni,

    sto preparando la soluzione, ma l'ultima parte la vorrei lasciare ancora in sospeso perché è molto carina... domani faccio uscire la prima parte.

  27. Francesco
    19/01/2021 at 19:22

    Che basti tracciare una sola retta nel triangolo equilatero?

    r_{1}=r_{2}=\frac{\sqrt[]{3}-1}{2}

    ?

  28. Francesco
    19/01/2021 at 20:26

    Ahi ahi ahi... no!

  29. leandro
    19/01/2021 at 20:34

    R=1/2 , faticoso ma sicuro.

  30. Vincenzo Zappalà
    20/01/2021 at 05:51

    mi spiace Leandro... troppo facile sarebbe... e poi ci vorrebbe la dimostrazione, comunque.

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.