Questo articolo fa parte della serie "Dante - Riemann - Einstein: Dio e il Big Bang" che è stata inserita nelle sezioni d'archivio "Cosmologia" e "Arte, letteratura e storia della scienza"

 

Iniziamo il nostro progetto verso l’Universo di Dante e quello di Riemann ed Einstein. La prima cosa da fare è cercare di rendere “visibile” e/o “immaginabile” un’ipersfera e lo faremo grazie all'aiuto di alcuni bacherozzi dotati di grande spirito d'osservazione e di intelligenza non comune!

Per farlo prendiamo due strade separate. La prima si dedica in più passaggi a cercare di rendere “visibile” e/o “immaginabile” un’ipersfera. La seconda alla “nascita” e all’evoluzione dell’eresia e alla parallela stasi della visione scientifica dell’uomo medioevale. Attraverso occitani e catari, questa storia ci porta a Dante. A quel punto le due strade si uniscono in un’unica visione globale che ci conduce fino all’Universo odierno e al significato più ampio di Big Bang. La lettera A vicino i numeri progressivi si riferisce alle trattazione geometrica e fisica e sarà gestita essenzialmente da Enzo. La lettera B si riferisce alla storia degli eretici e della visione del Cosmo fino a Dante Alighieri e sarà gestita da Barbara. A quel punto la A e la B si riuniranno in una sola trattazione. Il metodo "dualistico" usato assomiglia molto alla visione intrinseca di un abitante di una superficie sferica: strade che sembrano parallele e senza alcuna relazione tra loro sono  destinate a incontrarsi in un punto rappresentato dall'Universo di Dante.

Ipersfera matematica

Teoricamente dovrebbe essere l’approccio più difficile e, invece, come spesso capita, è il modo più rapido e generale per definire una problematica (risolverla è… un’altra cosa).

Vogliamo arrivare a definire un’ipersfera di n dimensioni e vogliamo perciò stabilire le caratteristiche fondamentali che possano applicarsi qualsiasi sia n.

Immaginiamo di vivere e lavorare solo in spazi euclidei (qualsiasi siano le loro dimensioni), ossia in quelli in cui due rette parallele non si incontrano mai e la somma degli angoli di un triangolo vale sempre 180°. Le eventuali equazioni (poche e banali, non preoccupatevi) sono, perciò, basate sulla geometria euclidea.

Per facilitarci il compito iniziamo discutendo un poco sul cerchio. Vi è sempre un po’ di confusione tra cerchio e circonferenza. In realtà, il cerchio è la parte piana delimitata da una linea curva detta circonferenza. Il cerchio ha quindi dei limiti ben stabiliti nel suo piano di esistenza, ossia dei chiari confini, rappresentati proprio dalla circonferenza: o si è dentro o si è fuori! La circonferenza, invece, è una curva composta, come tutte le sue sorelle linee, da una serie di punti che si susseguono con continuità. Essa, perciò, è del tutto simile a una retta, con la sola differenza che la retta non ha alcun limite e la sua lunghezza risulta infinita. La circonferenza, invece, ha una lunghezza ben stabilita, anche se  non ha limiti: potrei percorrerla centinaia  di volte e non troverei mai la sua fine. Possiamo definirla qualcosa di FINITO (si misura la sua lunghezza), ma di ILLIMITATO, dato che non esiste nessun limite geometrico che ne segni l’inizio o la fine.

Questo concetto sarà uno dei più importanti sia per la trattazione puramente geometrica sia per i risvolti che avrà nelle varietà di Riemann e nell’Universo di Einstein  (senza dimenticarci di Dante, ma questo è un discorso che si svolgerà a parte e che si congiungerà a tempo debito).

Cerchio e circonferenza, sono due esempi già estremamente indicativi. Il primo esiste nel piano, ossia nelle due dimensioni, ed è solo e soltanto una sua parte, delimitata da un chiaro confine, al pari di un quadrato, di un rettangolo, di un esagono o di qualsiasi altra figura piana. Permettetemi di usare un nuovo termine per definire il cerchio (per non creare confusioni in seguito): disco.

Fatemi anche dire una frase apparentemente banale, ma che risulterà più che importante tra pochissimo. Si può abitare in uno spazio a due dimensioni euclideo e incontrare una circonferenza, ma è possibile anche vivere perennemente sulla circonferenza.

Questo è un concetto fondamentale, che ripeteremo fino alla nausea e che già ci fa comprendere la differenza tra il bordo e l’interno di una sfera qualsiasi. Lasciatemelo ripetere ancora attraverso due amici bacherozzi in Fig. 1.

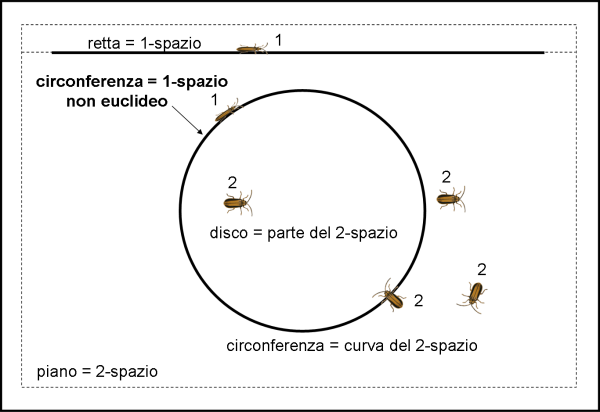
Uno è bello largo, ma piatto (2); l’altro è magro che di più non si può ed è comunque piatto (1). Il bacherozzo 2 vive nel piano della figura, ossia in un 2-spazio (spazio a due dimensioni euclideo) e può muoversi in ogni direzione. Se è dentro al disco o fuori dal disco rimane comunque a due dimensioni e vive nelle due dimensioni. Può anche attraversare la circonferenza (ossia entrare o uscire dal disco). La circonferenza è quindi parte del 2-spazio e può essere descritta perfettamente con la geometria euclidea del 2-spazio. Notiamo anche che il bacherozzo 2 vive in un 2-spazio infinito in ogni direzione. Il bacherozzo 1 vive invece soltanto in uno 1-spazio euclideo, la retta, che è infinita sia a destra che a sinistra. Inoltre esso può anche vivere sulla circonferenza che, in tal caso, per lui, diventa uno 1-spazio non euclideo finito e illimitato, perché, per descrivere la circonferenza, il bacherozzo 1 ha bisogno di una geometria diversa da quella (euclidea) che usava per descrivere la retta.

Passiamo, finalmente, alla definizione puramente matematica di  sfera a n dimensioni e vediamo se quanto detto finora trova un facile riscontro…

Sappiamo già bene come poter rappresentare la circonferenza in un piano euclideo con due sole coordinate x₁ e x₂ (le solite x e y, che adesso preferiamo chiamare con una sola lettera e con pedice diverso). Sia O l’origine degli assi x₁ e x₂ (le sue coordinate sono ovviamente x_1o = x_2o = 0). Una circonferenza con centro O e di raggio r, viene scritta in modo matematicamente compatto come:

(x₁ – x_1o)² + (x₂ –x_2o)² = (x₁ - 0)² + (x₂ - 0)² = r²

x₁² + x₂² = r²

Quanto scritto non è altro che il teorema di Pitagora (Fig. 2), scritto per ogni punto P della circonferenza in base alle due coordinate x₁ e x₂ del punto (l’ipotenusa è sempre r).

Ricordiamoci che siamo in uno spazio euclideo e Pitagora è ben accetto. Se invece volessimo descrivere il disco compreso dentro la circonferenza, dovremmo scrivere:

x₁² + x₂² ≤  r²

O, ancora meglio:

x₁² + x₂² <  r²

se volessimo proprio separare il disco dal suo bordo esterno.

Perché non provare subito a generalizzare queste formule, aumentando il numero di coordinate? In pratica, non faremmo altro che aumentare (o diminuire) il numero delle dimensioni dello spazio euclideo in cui stiamo descrivendo le nostre figure geometriche che parimenti cresceranno (o diminuiranno) in dimensioni.

Senza usare sommatorie e cose del genere, continuiamo con la matematica più elementare (in fondo, sempre e soltanto il teorema di Pitagora…) e scriviamo le formule generali:

x₁² + x₂² + x₃² + x₄² + … + x_n² = r²

x₁² + x₂² + x₃² + x₄² + … + x_n² < r²

Questa sono le rappresentazioni del nostro disco e della nostra circonferenza descritti in uno spazio a n dimensioni.

E’ giunta l’ora di generalizzare anche i nomi utilizzati. Anche se suona un po’ male, chiamiamo il disco, ossia la parte compresa dalla circonferenza,  n-palla, mentre chiamiamo il suo bordo (la circonferenza)  (n-1)-sfera.

Perché abbiamo scritto (n-1)? L’abbiamo già detto prima, attraverso i bacherozzi: per uno spazio a due dimensioni e, quindi, anche per la palla a due dimensioni (disco), il bordo, ossia la sfera relativa (circonferenza) ha, in realtà, una dimensione in meno: il disco ha due dimensioni, la circonferenza una sola, anche se l’abbiamo disegnata nel 2-spazio. Chi cammina sopra la circonferenza vive in una sola dimensione come chi cammina su una retta e non si accorge assolutamente della differenza. Ribadiamo che ogni n-palla è contenuta all’interno di una (n-1)-sfera. Un concetto semplice, ma da non tralasciare: uno spazio a n dimensioni può sempre essere contenuto in uno spazio con una dimensione in meno.

(Ciò che si mangia dell'arancia è il contenuto, ovvero la palla a tre dimensioni. La buccia di solito non si mangia, e la possiamo immaginare molto sottile al punto di avere solo due dimensioni.)

Senza quasi accorgercene abbiamo già introdotto, in modo molto leggero, le varietà di Riemann…

Vediamo se questa formula di estrema banalità va bene per altri valori di n. Cominciamo con il caso più semplice…

n = 1                1-spazio (spazio a 1 dimensione)

1-palla (palla a una dimensione)

x₁² < r²

ossia il segmento AB compreso tra – r e + r come indica la Fig. 3.

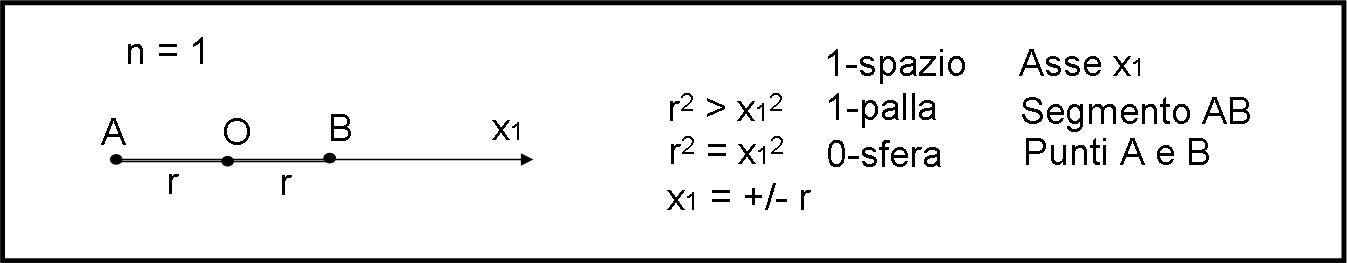
Alla 1-palla corrisponde (come bordo) una 0-sfera, data da:

x₁² = r²

ossia

x₁ = +/- r.

nient’altro che la definizione di due punti separati A e B. La sfera ha veramente 0 dimensioni, dato che è composta solo da due punti separati, tali da non permettere nessun movimento su di essi.

Passiamo a uno spazio a 2 dimensioni (che ormai conosciamo abbastanza bene…)

n = 2         2-spazio

x₁²  + x²₂ < r²             2-palla

e

x₁²+ x₂² = r²               1-sfera

La prima non è altro che l’equazione del cerchio (disco nel nostro caso ) o meglio della 2-palla. La seconda non è altro che l’equazione della circonferenza di raggio r nel piano delimitato dalle due coordinate x₁ e x₂, che è una 1-sfera, in quanto essa rappresenta una linea, ossia uno spazio a una dimensione (Fig. 4).

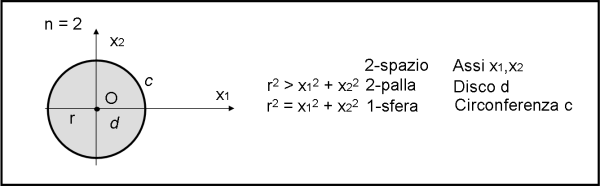
Fermiamoci solo un attimo e ribadiamo il concetto più importante: la 1-sfera corrisponde sempre a una 2-palla e ne rappresenta il bordo, ossia non è altro che una figura a 1 dimensione rappresentata nello spazio a 2 dimensioni. Non sbuffate per la ripetizione (non sarà l’ultima volta… ma questo punto è essenziale e se scappa di mano sono guai seri…).

Passiamo allo spazio in cui viviamo (o crediamo di vivere…), quello euclideo a tre dimensioni.

n = 3                    3-spazio

x₁²  + x₂² + x₃² < r²             3-palla

x₁²  + x₂² + x₃² = r²             2-sfera

I nomi non concordano con quanto ci viene insegnato a scuola e con il linguaggio comune. La 3-palla è proprio una palla con le sue tre dimensioni, ma viene normalmente chiamata sfera. Analogamente la 2-sfera è quella che chiamiamo superficie sferica e che contiene la 3-palla (Fig. 5)

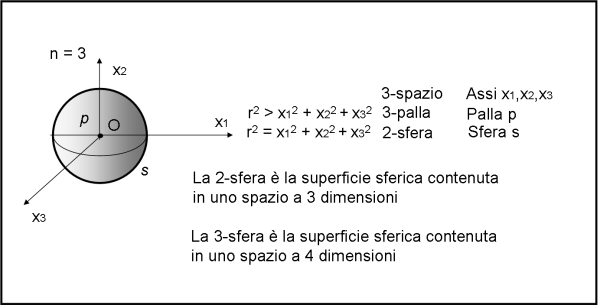
Facciamo un passetto in più (ma ricordiamoci anche quanto scritto QUI). Per disegnare una 2-sfera è comodissimo usare uno spazio a 3 dimensioni e le sue coordinate (come abbiamo appena fatto), ma è fondamentale ricordare che la 2-sfera resta a tutti gli effetti uno spazio a due dimensioni, così come lo è il piano euclideo. Bastano due coordinate per stabilire ogni punto su di essi per chi ci vive sopra. Sul piano le solite x e y (o x₁ e x₂), sulla 2-sfera qualcosa di diverso, come latitudine e longitudine (vedi anche QUI).

Ancora una volta, però, ricordiamo che il piano non ha limiti ed è infinito, mentre la superficie sferica non ha limiti ma è finita.  In altre parole, su un piano potremmo camminare per sempre e scoprire sempre nuovi luoghi, nella 2-sfera continueremmo a girare e molto probabilmente ci ritroveremmo prima o poi al punto di partenza.

Non stupiamoci, perciò, se la nostra Terra, dove pensiamo di eseguire misure sulla sua superficie, non è assolutamente una superficie euclidea (è ben diversa da un piano). La 3-palla è invece la terra nella sua interezza e lei può benissimo essere considerata una parte ben delimitata dello spazio a 3 dimensioni, limitato da una superficie non euclidea a due dimensioni  (non per niente si usa la latitudine e la longitudine per definire la posizione di un luogo).

Insistiamo anche su un  altro punto fondamentale. Se vogliamo “vedere” la 2-sfera nella sua interezza (visione estrinseca) siamo obbligati a rappresentarla immersa nello spazio a 3 dimensioni, quello che ci permette di rappresentare perfettamente bene la 3-palla, ossia ciò che sta “dentro” la 2-sfera. Se però vogliamo viverci sopra come un bacherozzo largo, ma piatto (come il numero 2), diciamo addio alla geometria euclidea e studiamoci la trigonometria sferica (QUI).

Eseguiamo il passo più critico e passiamo alle 4 dimensioni, ormai fuori dalla nostra portata visiva.

n = 4                   4-spazio

x₁² + x₂² + x₃² + x₄² < r²             4-palla

x₁² + x₂² + x₃² + x₄² = r²             3-sfera

Riprendendo il discorso appena fatto, questa equazione ci darebbe la perfetta descrizione della 3-sfera. Purtroppo, dovremmo potere usare 4 coordinate e con i nostri mezzi non è possibile, se non con la pura matematica. Per la visione grafica dovremo accontentarci di entrare su di essa, descriverla dal di dentro (basterebbe chiedere a Riemann) o cercare di vedere qualche sua proiezione sul piano o nello spazio euclideo a 3 o a 2 dimensioni. Una sua visione estrinseca è impossibile perché richiederebbe uno spazio a 4 dimensioni.

Siamo proprio nelle condizioni dell’Universo di Einstein: 4 dimensioni, in cui, bloccandone una (il tempo), siamo di fronte al nostro spazio inteso come superficie a tre dimensioni curva non euclideo. Riemann l’aveva trattato e descritto a fondo ed Einstein ci si è buttato “a pesce” per inserirlo nella sua equazione finale della RG. Un lavoro troppo arduo per noi e troppo “matematico”.  Tuttavia, vi sono delle possibilità di comprensione, molto limitate, ma sufficienti per chi ha immaginazione, fantasia e capacità di concentrazione, che possono permettere analogie facilmente comprensibili  e di facile estrapolazione. Ricordiamoci, anche, di non fossilizzarci sul tempo come quarta dimensione obbligatoria. Lo è sicuramente per il nostro Universo einsteniano, ma potrebbe essere una qualsiasi dimensione aggiuntiva, anche non... concreta (e Dante fa capolino…).

(un palloncino sferico che si gonfia o si sgonfia al variare della pressione può essere rappresentato nel suo sviluppo da una serie di immagini che hanno come parametro la pressione. Non si gonfia perché passa il tempo, ma "mentre" passa il tempo. La quarta variabile è la pressione).

Parliamoci chiaro: la 3-sfera è uno spazio a 3 dimensioni che, però, non risulta euclideo. Come già successo per la 2-sfera sappiamo che è uno spazio finito e illimitato. Approfondiamola, allora, attraverso le analogie che possiamo ricavare analizzando lo spazio non euclideo di una 2-sfera. Il passaggio a una dimensione in più non sarà così difficile, se lasciamo libera la nostra immaginazione.  Una 2-sfera può essere compresa e studiata sia attraverso le sensazioni di un abitante che ci vive sopra, sia attraverso ciò che riesce a vedere di lei un abitante di uno spazio euclideo a 2 dimensioni, ossia di un piano. Per la seconda possibilità, niente di meglio che rifarci direttamente a quel piccolo grande capolavoro che è Flatlandia di Abbot.

 

Se pensate che sia impossibile disegnare in quattro dimensioni, leggete QUI