Categorie: Matematica Teoria degli insiemi
Tags: crittografia curve ellittiche
Scritto da: Umberto Cibien
Commenti:0
Il campo Zp: Una applicazione al DLP, ovvero il problema del logaritmo discreto **/***
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Il DLP è una sigla inglese che deriva da Discrete logarithm problem, che significa problema del logaritmo discreto. Vedremo che legame ha con quello che abbiamo trattato sul campo Zp .
Il gruppo ciclico Zp.
Consideriamo il campo Zp con p primo visto nell'articolo precedente Campi algebrici. Essendo Zp un campo, in particolare è un gruppo moltiplicativo. Lo abbiamo dimostrato nel caso in cui p è un numero primo.Quindi ogni elemento in Zp ha un inverso, ossia dato esiste sempre
tale che
. Ricordiamo poi Zp è un gruppo finito con ordine p, ossia p è il numero di elementi distinti del gruppo. Gli elementi di Zp possono essere indicati semplicemente cosi: Zp={[0],[1],[2],[3],[p-1]}.
Come di consueto indichiamo con [a] la classe di equivalenza modulo p , dove abbiamo preso come rappresentante a per indicare tutti i numeri che danno lo stesso resto divisi per p. Se p=5, [2] rappresenta tutti gli interi che divisi per 5 danno resto 2; essi sono ad esempio 2,7,12,17,.. ecc.
In questo articolo abbiamo trattato i gruppi finitamente generati e i gruppi ciclici. Adesso è giunto il momento di darne una applicazione.
Supponiamo p=5 ; se indichiamo l'ordine di un gruppo G con O(G) (ordine di un gruppoè finito è il numero dei suoi elementi), allora O(Z5)=5
infatti Z5={[0],[1],[2],[3],[4]}. L'insieme degli elementi invertibili di Zp, ossia O(Zp\{0}) ha ordine p-1, quindi nel nostro caso l'ordine è4.
Dobbiamo infatti togliere lo zero, che non ha inverso, ma anche Zp\{0} è un gruppo, sottogruppo di Zp.
Diverso concetto è l'ordine di un elemento di un gruppo. Se g appartiene ad un certo gruppo G, definiamo ordine di g (e lo indichiamo con o(g)) il minimo intero m tale che:
; ricordiamo che con tale espressione indichiamo il prodotto di g per se stesso m volte:
m volte. C' è un legame molto stretto fra l'ordine di un gruppo e l'ordine di un elemento; se esiste un elemento il cui ordine è uguale a quello del gruppo, tale elemento diventa generatore del gruppo, e il gruppo diventa ciclico. Cosa vuol dire questo intuitivamente? Che se moltiplico un elemento per se stesso a un certo punto ritrovo gli stessi valori, oltre che a generare tutti gli elementi del gruppo. Ma vediamomolo con un esempio:
Consideriamo Z5.
In questo caso p=5 è primo, quindi Z5 senza lo zero è un gruppo moltiplicativo.
i suoi elementi diversi da zero sono:
[1][2],[3],[4]l'ordine di[1] è chiaramente 1.
vediamo che ordine ha [2] [2] [2]*[2]=[4] [2]*[2]*[2]=[8]=[3] [2]*[2]*[2]*[2]=[16]=[1] (se adesso continuo a moltiplicare per due ritrovo la stessa sequenza)
l'ordine di[2]è 4 e come vediamo [2] è un generatore di Z5\{0}; infatti le sue potenze da 1 a 4 =5-1=p-1 generano tale gruppo. Chiaramente se proseguo nelle moltiplicazione,riottengo gli stessi valori.
quindi Z5 è ciclico e [2] è un suo generatore.
Il problema del logaritmo discreto; caso generale.
si G un gruppo ciclico di ordine n e g un suo generatore.
Sappiamo allora che ogni elemento di G può essere espresso come potenza di g ovvero come
g*g*g...g* un certo numero di volte. Sia y un certo elemento di G e diverso da 1.
Quindi , essendo G ciclico con generatore g, si ha:
per qualche x intero,
(x deve essere minore di n, in quanto
)
Ebbene, x si chiama logaritmo discreto di y, e possiamo chiamare g base del logaritmo. Che differenza c'è fra il logaritmo che conosciamo dalle superiori? Bè, la definizione è la stessa, cambia il campo di applicabilità; il logaritmo generico viene definito per qualsiasi numero reale positivo, mentre qui ci troviamo in genere in un gruppo finito di elementi, da cui l'aggettivo "discreto". Capirete poi che il valore dipende anche da come definiamo la moltiplicazione nel gruppo. Il DPL resta comunque un problema, da risolvere con un certo algoritmo. Notiamo il fatto che affinchè il DLP abbia soluzione è necessario essere in un gruppo ciclico,ovvero in un gruppo in cui ogni elemento può essere ricavato da potenze di un suo elemento.
Il problema del logaritmo discreto; caso Zp con p primo.
Torniamo al nostro gruppo Zp, con p primo. Dalle considerazioni fatte soprasappiamo xhe è un gruppo ciclico. Ci proponiamo adesso di risolvere il problema del DPL in qualche caso particolare. Prendiamo Z5 con g=[2] che abbiamo visto essere un generatore di tale gruppo. Supponiamo che sia
ovvero
come facciamo a trovare x? potremmo confrontare x con i calcoli fatti sopra dove cercavamo l'ordine di [2]:
[2] [2]*[2]=[4] [2]*[2]*[2]=[8]=[3] [2]*[2]*[2]*[2]=[16]=[1]troviamo che x=2;
Nelle applicazioni (vediamo dopo quali) il primo p è un numero molto grande; capirete anche voi che questo non è un granchè come metodo, dovremmo ogni volta calcolare tutte le potenze di un certo numero e confrontarle con il numero dato , fino a trovare x. Nei casi applicativi che vedremo più avanti l'ordine di un gruppo è molto alto, circa ; nel caso peggiore dovremmo confrontare tutti gli elementi del gruppo, e l'operazione diventa impossibile (ci vorrebbero anni). Quindi già in Zp il DLP è un problema difficile,mentre il calcolo delle potenze di g è un problema relativamente facile e veloce. Ma a cosa serve tutto questo?
Una semplice applicazione alla crittografia.
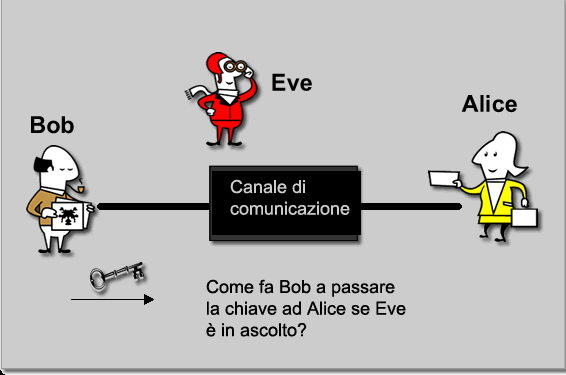
La crittografia è la scienza che si occupa di mascherare il passaggio di informazioni. Al mondo d'oggi tutto può essere trasformato in numeri; immagini, voci , codici di carte di credito, ecc. Si tratta di riuscire a trasferire tramite un canale di comunicazione questo scambio di informazioni in modo sicuro.
Useremo per la descrizione dei personaggi consolidati e standard nel campo della crittografia: Alice, Bob ed Eve. Eve rappresenta il nemico,il malintenzionato che spia le comunicazioni fra Alice e Bob.
C'è un metodo semplice per uno scambio di chiavi che poi diventa anche sicuro grazie al DLP. Intanto cos'è una chiave? E' ciò che ci consente di decifrare un messaggio . Ci sono vari metodi per cifrare attraverso delle chiavi . Noi ci occuperemo per ora solo dello scambio sicuro di chiavi.Una volta scambiata in modo sicuro la chiave, si può procedere alla cifratura/decifratura del messaggio.
Un metodo semplice (che è alla base di quasi tutti i protocolli) è questo:
Alice e Bob scelgono pubblicamente un primo p per il gruppo Zp e un elemento g che genera il gruppo Zp
Bob sceglie casualmente a , 2<=a<=p-2 calcola e invia il risultato A Alice
Alice sceglie casualmente b , 2<=b<=p-2 calcola e invia il risultato B a Bob
BOB calcola (problema facile,calcolo di una potenza)
Alice calcola
Chiaramente
Si considera quindi K come chiave;
Esempio: p = 23, g = 5. Ci troviamo quindi in Z23 con generatore g=5.
Alice sceglie a = 6 (679*23+8=15625)
Bob sceglie b = 15 (1326851222*23+19=30517578125)
Alice calcola
Bob calcola
E Eve? Eve oltre a A, B può conoscere g e p; per calcolare
deve calcolare prima a,b e quindi risolvere il problema del DLP in entrambi i casi, ovvero e
. Ma questo è un problema difficile, come abbiamo visto.
La sicurezza si questo tipo di protocollo dipende quindi dalla difficoltà del DPL,e quindi dal gruppo in cui ci troviamo. Già Zp con il prodotto modulare è abbastanza sicuro, ma ci sono algoritmi più efficienti dal punto di vista del calcolo di e ancora più sicuri come DLP; anche a questo serviranno le curve ellittiche, oltre ad introdurci nei punti salienti della dimostrazione del teorema di Wiles/Fermat.