Io riporto una soluzione, ma può darsi che ne esistano anche altre, magari più eleganti e rapide.

Do per acquisite alcune costruzioni "classiche" alla greca, ossia eseguite con riga non graduata e compasso "molle", ossia tale che non può essere usato per riportare una distanza. Di queste ne abbiamo parlato qua e là, ma se vi sembra interessante potrei dedicargli un articolo apposito (fatemi sapere...).

Iniziamo col tracciare una circonferenza di centro C e un suo diametro AB. Il primo passo da fare è quello di dividere AB in sette parti uguali.

Ciò  è sempre possibile: basta tracciare una retta qualsiasi passante per A, scegliere un punto P qualsiasi su di essa, e poi fare centro in P e tracciare  la circonferenza di raggio AP. In tal modo si determina il punto Q sulla retta r che ha una distanza da P tale e quale alla distanza AP. Si procede così fino ad ottenere un certo punto R, tale che il segmento AR sia  diviso in 7 parti uguali (Fig. 1).

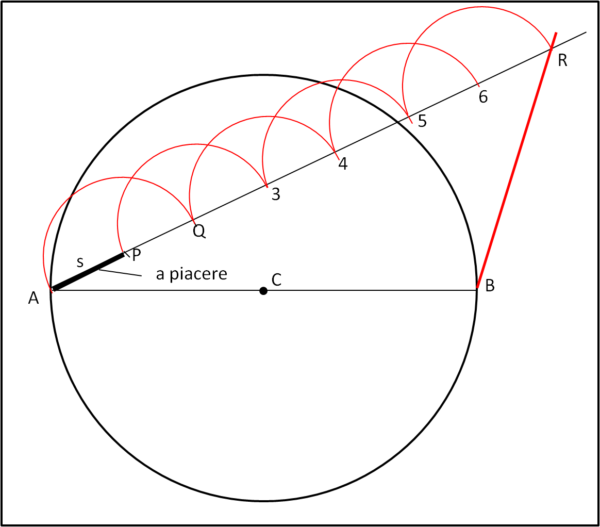
A questo punto basta unire R con B e tracciare dai punti della retta r le parallele a RB. Tracciare una parallela a una retta che passi per un punto è una delle costruzioni classiche. Le parallele così tracciate individueranno i punti neri sul segmento AB tali da dividere AB in 7 parti uguali (Talete insegna...), come mostrato in Fig. 2.

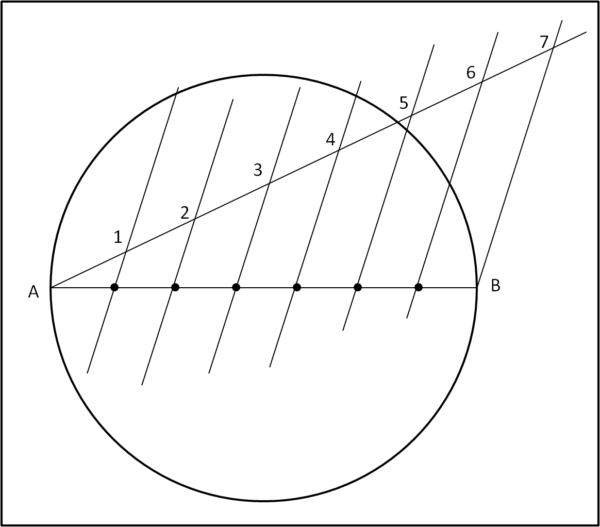
Non è difficile, adesso, dividere ogni intervallo tra punti neri in due parti uguali, ossia trovare i punti di mezzo (rossi). Dato un segmento è costruzione classica trovare il loro asse e, quindi, il punto di mezzo. Otteniamo la Fig. 3.

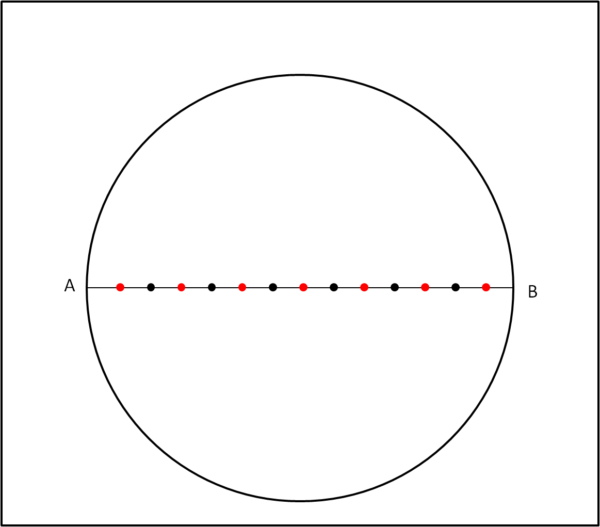
A questo punto, inizia la parte più "fantasiosa", ma precisa. Facendo centro nel primo punto rosso da sinistra, tracciamo il semicerchio di raggio uguale alla distanza di questo punto da A. Per semplicità diamo a questo raggio il valore 1. Poi tracciamo il cerchio con centro nel primo punto nero, tale che il suo raggio sia uguale alla distanza tra questo punto e A. Continuiamo così fino a tracciare il cerchio di partenza, quando viene fatto centro nel centro del cerchio. La Fig. 4 illustra il procedimento...

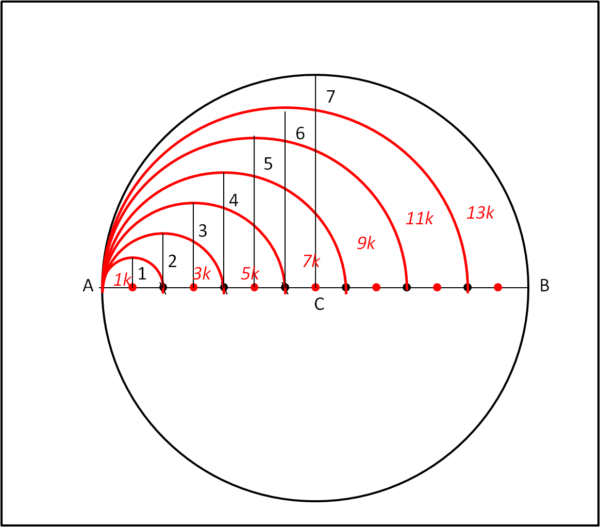
Notiamo subito che i raggi dei vari semicerchi hanno valori che vanno da 1 a 7, per costruzione. Ogni loro area vale quindi πr_n²/2 con n che va da 1 a 7, così come r_n. Chiamiamo π/2 = k

Aree semicerchi = 1²k, 2²k, 3²k, 4²k, 5²k, 6²k, 7²k

E' immediato calcolare le aree racchiuse tra due semicerchi:

12k =         1k

2²k- 1² k= 3k

3²k - 2²k= 5k

4²k - 3²k= 7k

5²k - 4²k= 9k

6²k - 5²k= 11k

7²k - 6²k= 13k

Il gioco è praticamente fatto...

Basta, infatti, ripetere l'operazione appena fatta, partendo da B e andando verso A, con semicerchi (azzurri) che stiano nella parte passa del cerchio di partenza, come mostra la Fig. 5.

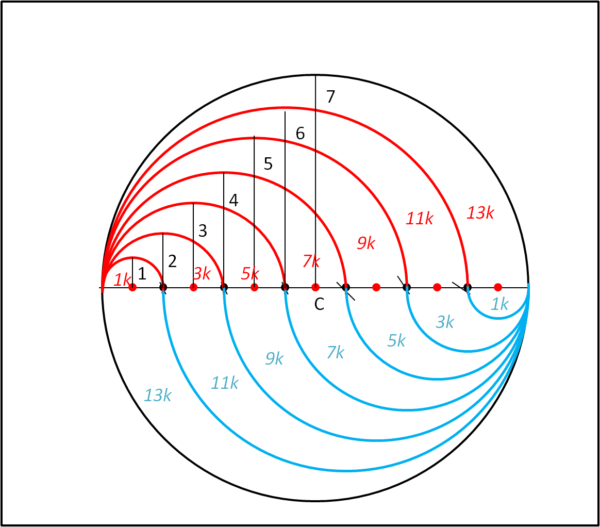
Le aree racchiuse tra i semicerchi azzurri sono identiche a quelle costruite nella parte superiore. Per cui basta sommare tra loro quelle corrispondenti:

1k + 13k = 14k

3k + 11k = 14k

5k + 9k =  14k

7k + 7k =  14k

9k + 5k =  14k

11k + 3k = 14k

13k +  k =  14k

In poche parole abbiamo diviso il nostro cerchio in 7 parti di area perfettamente uguale e pari a:

Area = 14 k = 14 π/2 = 7 π

Moltiplicata per 7 diventa 49 k che è proprio l'area del cerchio di partenza.

E gli antichi greci sono contenti...

Il quiz lo trovate QUI