Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

La conservazione del momento angolare è un fenomeno che tutti conosciamo in quanto è proprio quello che fa girare sempre più veloce una pattinatrice sul ghiaccio, se avvicina le braccia al corpo. E’ lo stesso fenomeno che fa girare le stelle di neutroni come trottole impazzite. Ma i suoi giochi sono molteplici...

Dico subito che si poteva rendere l'esperimento molto più pratico,  pensando direttamente una persona seduta su una sedia girevole. Il disegno, però, diventava complicato e allora ho schematizzato la situazione, come mostrato in Fig. 1.

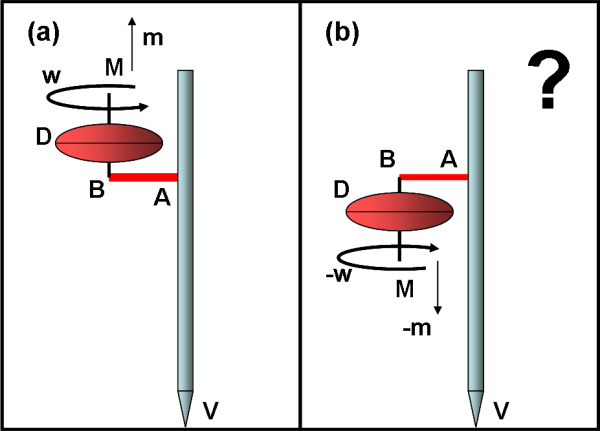
Consideriamo in Fig. 1(a) una bella matitona azzurra in posizione verticale, con la punta V che tocca il pavimento, ovviamente perfettamente liscio. Su di essa inseriamo una piccola barra AB, che può essere fatta ruotare attorno ad A, ma che una volta ruotata può nuovamente essere bloccata. Sulla sua estremità B inseriamo un’altra barra MB che può girare attorno a B. Ovviamente, in B vi è una specie di cerniera che permette la rotazione ma che tiene ancorate MB e BA. Inseriamo un disco D dentro alla barra  MB e mettiamolo in rapida rotazione attorno a MB.

Il disco può ruotare, ma non può scorrere su e giù lungo l’asse di rotazione MB. Immaginate  che il disco sia, ad esempio, una ruota di bicicletta che gira intorno al suo asse MB. Tutto deve essere perfetto (non vi sono attriti o angoli strani). La situazione è perfettamente stabile. L’unica cosa che si muove è la trottola che gira attorno al suo asse. Essa può continuare a ruotare per un tempo lunghissimo senza mai rallentare.

Come vi dicevo, non è difficile pensare che la matita sia uno di voi seduto su una sedia girevole. AB è un vostro braccio e MB è l’asse di una ruota di bicicletta D che ruota velocemente. Il sistema matita (persona + sedia) e disco rotante (ruota di bicicletta) è  perfettamente stabile. Esso avrà un certo momento angolare, dato che vi è una rotazione.  Il suo momento angolare è diretto verso l’alto ed è rappresentato dal vettore m. Esso vale Iω, dove I è il momento d’inerzia e ω è la velocità di rotazione. Tuttavia, non preoccupatevi più di tanto della formula e pensate solo a cosa capita praticamente. Per chi ne avesse bisogno, di momento angolare abbiamo a lungo parlato QUI oppure nel libro "La Fisica Addormentata nel Bosco".

A questo punto, facciamo un piccolo cambiamento alla configurazione precedente. Mantenendo sempre il disco (la ruota) in rotazione, ruotiamo l’asse MB di 180° rispetto a prima. Il disco continua a ruotare, ma -ovviamente- in senso contrario (l’ho ribaltato…). Il suo momento angolare è sempre m, ma con segno opposto, ossia diretto verso il basso, come indica la Fig. 1(b).

Tutto sembra di nuovo perfettamente stabile e in equilibrio. Ne siete veramente sicuri? Purtroppo no! Il momento angolare del disco ha cambiato di segno! Non si può permettere un cambiamento del genere senza colpo ferire. Perché? Ovvio: il momento angolare del sistema non si è assolutamente conservato, mentre invece doveva farlo! La figura non è quindi giusta. Manca qualcosa di veramente importante. Che cosa?

NB: Se volete provare a rispondere prima di continuare a leggere, potete anche farvi aiutare dall’esecuzione pratica dell’operazione (basta una sedia girevole e una ruota di bicicletta).

 

Il succo finale è la conservazione del momento angolare del sistema totale. Di esso fanno parte matita + braccio + ruota. Qualsiasi movimento venga fatto al suo interno (senza intrusioni di forze esterne), il momento angolare deve restare sempre lo stesso.  Qualcosa di simile lo vediamo nel Sistema Solare dove devono giocare momenti angolari orbitali e momenti angolari di rotazione. Alla fine, se non arriva qualcosa da fuori rispetto al sistema solare che cambi il momento angolare, tutto ciò che capita al suo interno deve riportare il momento angolare finale al valore iniziale. Fortunatamente, nel caso trattato da questo articolo, la faccenda è molto più semplice.

Quali sono le condizioni di partenza?  Un solo momento angolare applicato al sistema: la ruota che gira in senso antiorario. Il suo momento angolare m è, quindi, diretto verso l'alto. Ripeto: questa è la configurazione di partenza e questo è il momento angolare che si deve conservare. Tutto il resto è  immobile. Se, adesso, ribalto la ruota, ribalto anche il momento angolare che adesso diventa -m (la ruota gira in senso orario). Deve succedere qualcosa, dato che il momento angolare non si è conservato per niente: il suo verso è importantissimo perché inverte il senso di rotazione: la fisica deve intervenire.

ATTENZIONE: il momento totale non deve cambiare perché non è arrivata nessuna forza dall'esterno del sistema a modificarlo. Il ribaltamento della ruota è stato fatto all'interno del sistema e quindi deve essere compensato. Se fosse arrivata una pallina da fuori, e avesse colpito la matita e/o la ruota, avrebbe cambiato completamente le cose, ma avrebbe anche cambiato il momento angolare totale.

Nel nostro caso, no. Abbiamo fatto tutto "in famiglia". Cosa bisogna allora introdurre per compensare il ribaltamento del momento angolare m? Facile, introdurre un momento angolare di segno opposto e di modulo doppio, ossia uguale a  + 2m. A questo punto basta fare una somma di momenti angolari e verificare che si è tornati alle condizioni originali, ossia abbiamo conservato il momento angolare totale del sistema:

-m + 2m = +m        esattamente come in Fig. 1(a)

Un momento angolare, però, deve essere applicato a qualcosa che è libera di ruotare. L'unica cosa che abbiamo è la matita che può girare su se stessa (ossia l'uomo che può girare con la sedia).

 

 

Essa ovviamente si porta dietro tutto il sistema che è ancorato ad essa. Ed ecco quindi che ribaltando la ruota, la matita inizia a ruotare in senso antiorario portandosi dietro braccio e ruota (che continua a girare). Solo così si conserva il momento primitivo. La figura corretta è quindi la Fig. 2

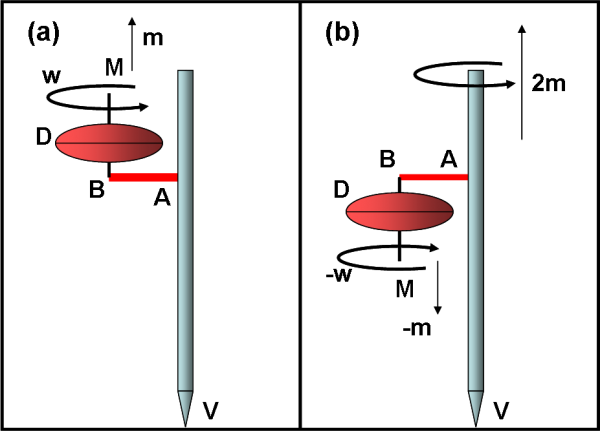
E se ribaltassi di nuovo la ruota? Ovvio... mi fermerei, dato che il momento angolare è tornato quello iniziale e la rotazione della matita non serve più.

E se, invece, le condizioni iniziali fossero state ruota ferma e matita ferma, il momento angolare del sistema era nullo. Se metto in rotazione la ruota, introduco un m o un -m (a seconda del verso) e quindi la matita inizia a girare in un verso o nell'altro in modo che:

m - m = 0        dato che 0 è la condizione iniziale, ossia il momento angolare totale originale.

Se, invece, la matita è bloccata e non può ruotare, sarà impossibile invertire il senso di rotazione del disco senza applicare una forza. Ma, in questo caso, il momento angolare non si conserverà. Possiamo vedere un'applicazione pratica nel video che segue:

Il momento angolare è una grandezza fisica fondamentale ed è l'equivalente della quantità di moto nei sistemi in rotazione. Come la quantità di moto è data dal prodotto della massa per la velocità, così il momento angolare è dato dal prodotto tra momento d'inerzia (legato alla massa) e velocità di rotazione.

P.S.:  attenzione a non confondere momento di una forza con momento angolare introdotto da questa forza. Il momento di una forza è equivalente alla forza, mentre -ripeto- il momento angolare è equivalente alla quantità di moto. La forza non è altro che una quantità di moto che varia nel tempo in quanto varia la velocità. Il momento di una forza non è altro che il momento angolare che varia nel tempo, in quanto varia la velocità di rotazione. Non per niente, in fisica, abbiamo la conservazione della quantità di moto e la conservazione del momento angolare (se non intervengono forze esterne, o momenti di forze esterni, che fanno variare le velocità sia lineari che angolari).

 

E, se avete ancora qualche dubbio sulla conservazione del momento angolare, potete chiedere spiegazioni ai nostri a-mici volanti!