Categorie: Corpi minori Matematica
Tags: asta rigida asteroide astroide geometria ipocicloide tecnologia
Scritto da: Vincenzo Zappalà
Commenti:2
Costruiamo un asteroide ! **
Questo articolo è stato inserito nella sezione d'archivio "Matematica e Geometria"
Sono diventati i personaggi del momento... Chi? Loro, proprio quei corpi piccoli, brutti e cattivi che chiamiamo asteroidi. Bene, non c'è momento migliore per costruirne uno in casa nostra!
La costruzione consta di varie fasi, che possono anche essere riprodotte su un foglio di carta. Iniziamo con un po' di "alta tecnologia" e poi rifugiamoci nei grafici (con cui ho maggiore dimestichezza).
Il primo passo è prendere un'asta rigida e fare muovere i suoi estremi lungo due rette perpendicolari tra loro. La domanda a cui rispondere è molto semplice: "Come si muovono i vari punti dell'asta?". Chi vuole può anche passare alla prova pratica, gli altri possono risolvere il gioco con qualche formuletta... Ce n'è per tutti i gusti.
Una volta tanto ho voluto fare il "tecnologo" (oh, povero me!) e ho disegnato il marchingegno di Fig. 1.
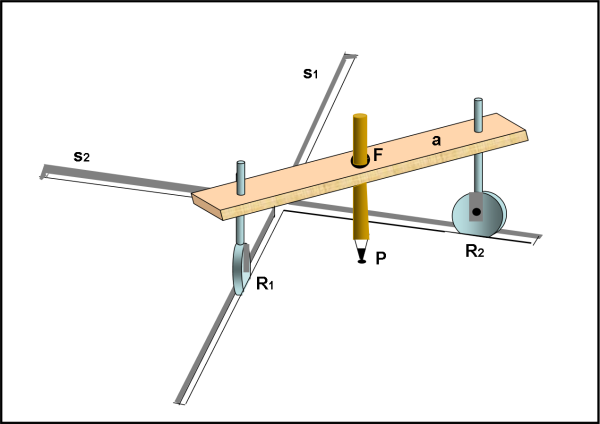
Vedo già molti rabbrividire e sicuramente sapranno fare moooolto meglio (li invito a inserire versioni all'altezza della tecnologia odierna...).Presa la nostra asta a, anche di legno, bisogna fare in modo che ai due estremi vi siano delle rotelline R1 e R2 che mantengano un moto lungo una sola direzione (si muovono lungo i propri binari o incisioni s1 e s2), mentre l'asta può ruotare mantenendo la sua lunghezza. In un punto qualsiasi dell'asta si può fare un foro F, in modo da introdurre una matita che lasci un punto P per tutte le diverse posizioni ottenibili dalle rotelle e quindi dell'asta. Che tipo di curva sarà descritta dal punto P?
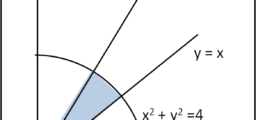
Per quanto mi riguarda, faccio molto prima a disegnare la configurazione che c'interessa in Fig. 2, mantenendo le stesse notazioni precedenti. Le due rotaie s1 e s2 le facciamo coincidere con gli assi cartesiani x e y.Possiamo tranquillamente considerare la lunghezza dell'asta L uguale a 1.
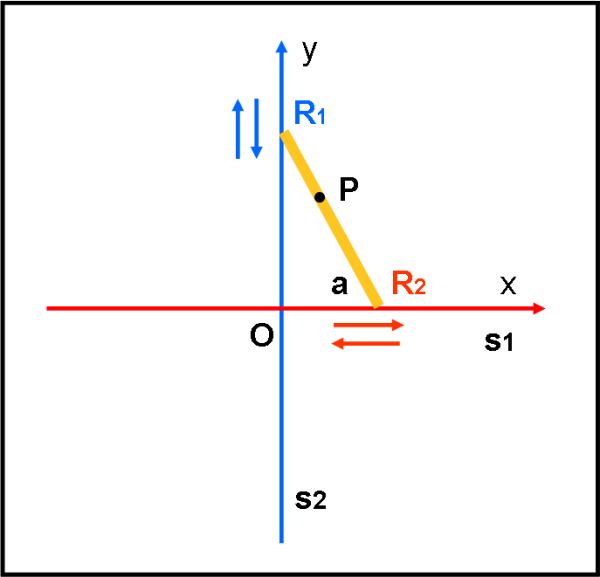
Possiamo risolvere il problemino disegnando l'asta in moltissime posizioni diverse e segnando il punto P corrispondente.
Invito tutti a far variare il punto P (quello che corrisponde a F) lungo l'asta rigida a partire da R1 fino a giungere in R2. In altre parole la distanza tra R1 e P può andare da 0 a 1 (lunghezza dell'asta), passando per R1P = 1/4, 1/3, 1/2, 2/3, 3/4 per finire con R1P = 1.
Non è certo impossibile, però, scrivere l'equazione generale della curva con il punto P messo in posizione qualsiasi e poi verificare caso per caso quanto trovato precedentemente .
Infine, nel caso più generale, si riesce a costruire tutta una serie di curve che ha per inviluppo proprio ciò che vogliamo ottenere.
Una delle possibili strade per la soluzione generale è la seguente (Fig, 3):
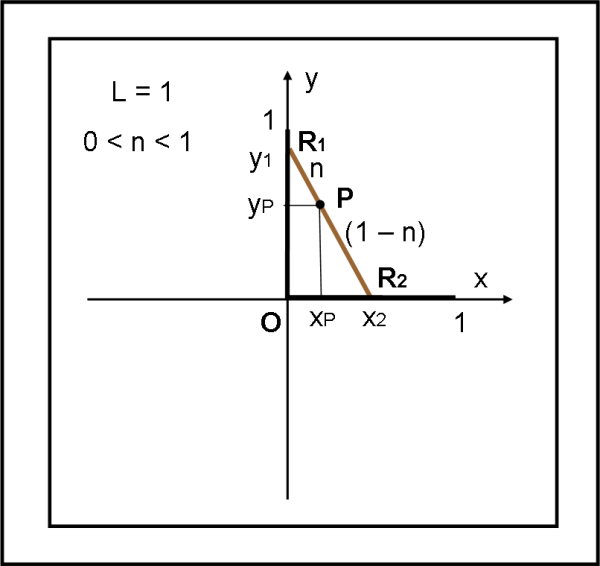
Il punto R1 ha coordinate (0, y1), mentre R2 ha coordinate (x2,o). Il punto P viene scelto come punto qualsiasi dell'asta R1R2 di lunghezza 1. Esso divide l'asta in due parti di lunghezza n e (1-n), dove 0 < n < 1. Per n = 0 e n = 1 cadiamo nei due casi degeneri. Per n = 0, P = R1; per n = 1 P = R2.
Le coordinate dei tre punti R1, R2 e P sono:
R1 (0,y1)
R2 (x2,0)
P (xP, yP)
Dai triangoli simili R1R2O e R1Py1, possiamo scrivere:
y1/1 = (y1 - yP)/n
n y1 = y1 - yP
yP = (1 - n) y1
y1 = yP/(1 - n) .... (1)
e
xP/n = x2/1
x2 = xP/n .... (2)
Applicando il teorema di Pitagora al triangolo R1OR2 si ha:
x22 + y12 = 1
Ricordando la (1) e la (2), si ottiene:
xP2/n2 + yP2/(1 - n)2 = 1 .... (3)
Che non è altro che l'equazione di un ellisse di semiassi n e (1-n).
Nel caso in cui n = 1/2
Si ottiene:
xP2 + yP2 = 1/4
Ossia, la circonferenza di centro O e raggio uguale a 1/2. Alcune ellissi e il cerchio sono disegnate in Fig. 4
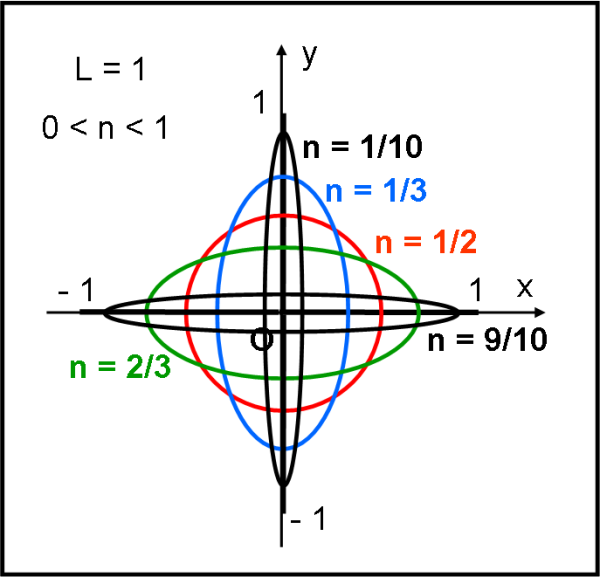
Veniamo alla parte più interessante...
La Figura 4 ci mostra una serie di ellissi tali che la somma dei loro semiassi sia sempre uno. L'inviluppo di tali ellissi ha un nome a noi (a me, in particolare), molto familiare: ASTEROIDE (o Astroide). L'animazione di Fig. 5 ci mostra molto bene la relativa costruzione:
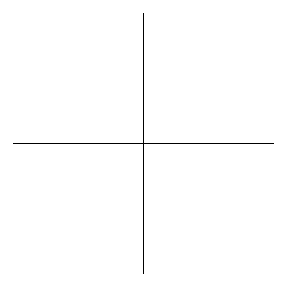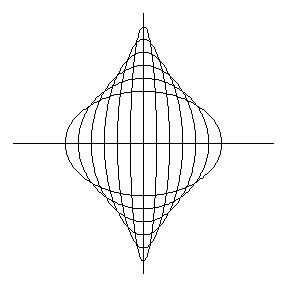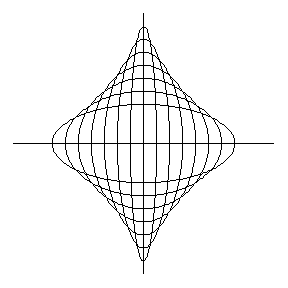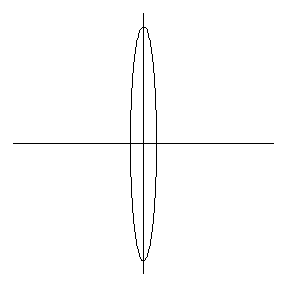
La stessa curva si ottiene come inviluppo della serie di segmenti di lunghezza unitaria che abbiano i loro estremi scorrevoli lungo i due assi cartesiani, proprio come abbiamo fatto noi fin dall'inizio. Lo vediamo in Fig. 6:
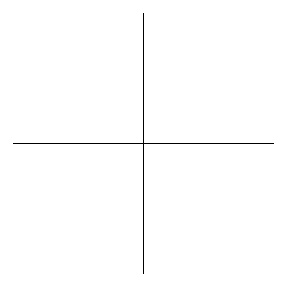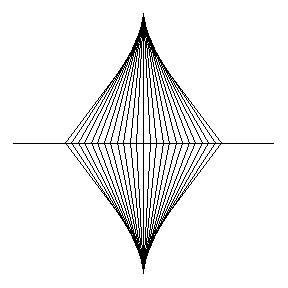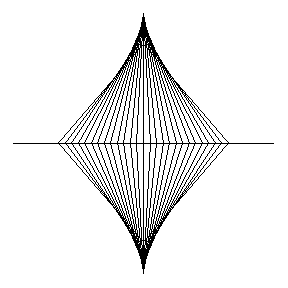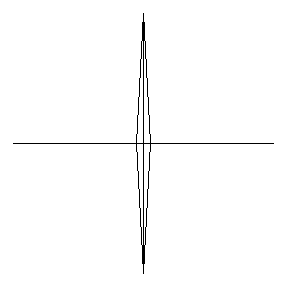
La costruzione si vede ancora meglio in Fig. 7:
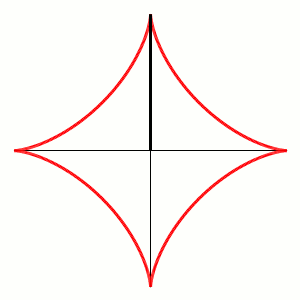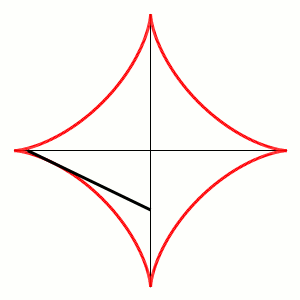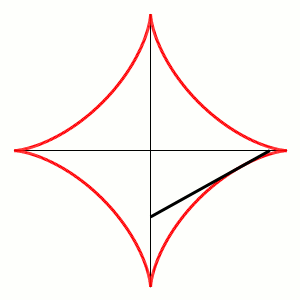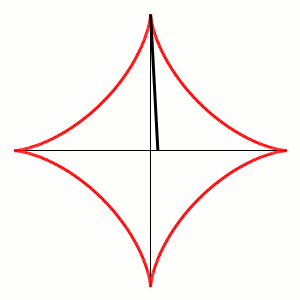
La cosa più bella è, però, che la stessa figura si ottiene come ipocicloide (QUI tutti gli articoli su cicolidi e simili)! Basta vedere l'animazione che segue nella Fig. 8
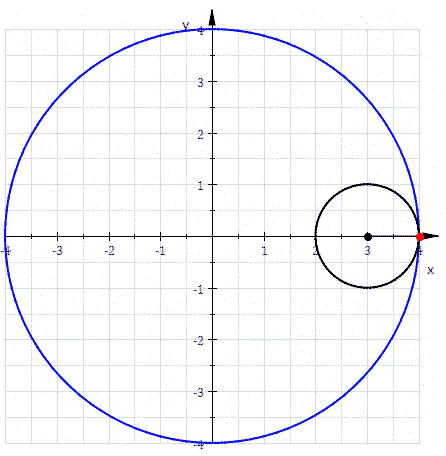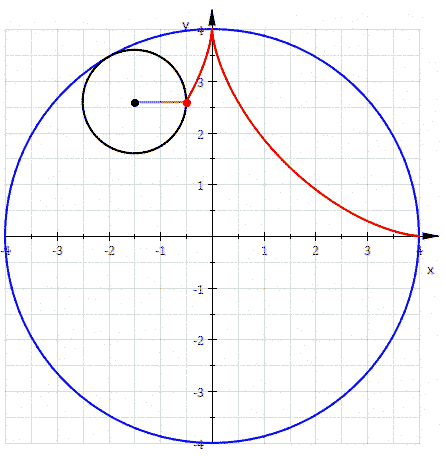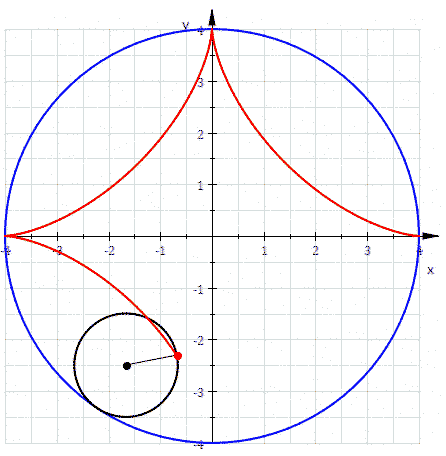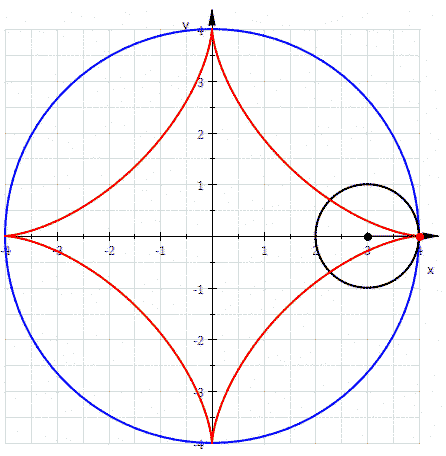
A questo punto, chi proprio lo desidera può anche cercare di ricavare l'equazione dell'asteroide e penso proprio che qualcuno lo farà...
NEWS! - Infatti qualcuno lo ha fatto e l'equazione dell'asteroide la trovate QUI
E chi desidera approfondire la conoscenza degli asteroidi "veri", può farlo QUI



2 commenti
Sì, sì, gioca a fare il tecnologo, lui... Poi le formule le lascia sul gobbo degli altri.
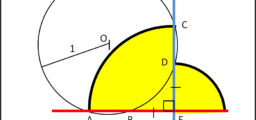
Ecco una prima figura che illustra la costruzione della curva. La circonferenza che rotola ha diametro metà di quella ferma.
La posizione I è quella iniziale e la F quella Finale. La lettera C rappresenta il centro della circonferenza mobile e la T è il punto di contatto tra le due circonferenze.
A seguito della rotazione dell'angolo alfa il punto si muove dalla posizione I alla posizione P mentre la circonferenza mobile compie una rotazione beta che è esattamente il quadruplo di alfa,
Chiamando r il raggio del cerchio fisso, il raggio di quello mobile vale r/4
Ecco le espressioni di x e y in funzione di r e di alfa
Analogamente scrivo l'espressione della y
passando ad esprimere le precedenti equazioni in funzione dell'angolo complementare di , ossia l'angolo
, ossia l'angolo  , riferito alla coordinata orizzontale, scrivo:
, riferito alla coordinata orizzontale, scrivo:
Ora queste due equazioni sono parametriche in e posso eliminare il parametro nel modo seguente:
e posso eliminare il parametro nel modo seguente:
elevo entrambe alla potenza di 2/3 , ottenendo
Ora, sommando le due equazioni ottengo
Non a caso questa equazione ha una struttura che ricorda una ellisse...
Ma ricorda anche una retta...
Insomma sono tutte riconducibili alla forma seguente
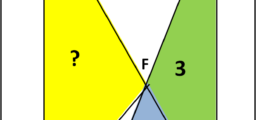
Concludo con una figura che mostra come costruire per punti, con riga e compasso l'asteroide o ipocicloide che dir si voglia.
Per ogni raggio, diversamente inclinato, ricavo il corrispondente punto P.
E per i fanatici di cicloidi, epicicloidi e asteroidi, non dimentichiamoci di questo link...
http://www.infinitoteatrodelcosmo.it/2018/02/20/soluzione-dei-quiz-sulle-monete-rotolano/