Categorie: Relatività
Tags: Campi scalari Campi vettoriali derivata covariante gradiente Simboli di Christoffel
Scritto da: Fabrizio
Commenti:4
Mettiamoci alla prova con la Relatività Generale - la derivata covariante
Questo articolo fa parte della sezione "METTIAMOCI ALLA PROVA!" all'interno della Relatività Generale al microscopio
In questo articolo riprendo gli argomenti trattati da Enzo nell'articolo “La derivata non conserva l'uguaglianza” della serie “La relatività generale al microscopio” proponendoli nelle loro versioni applicate alle coordinate cartesiane ed alle coordinate polari.
L'oggetto principale dell'articolo di Enzo è la derivata covariante dei tensori. Questo argomento richiama molti dei temi trattati negli articoli precedenti.
Per arrivare alla derivata covariante ho pensato di proporre un percorso che ricapitola questi temi con alcuni esempi.
Riassumo qui di seguito il contenuto di questo articolo. Spero che possa essere una traccia che aiuti a seguire e legare i vari argomenti toccati.
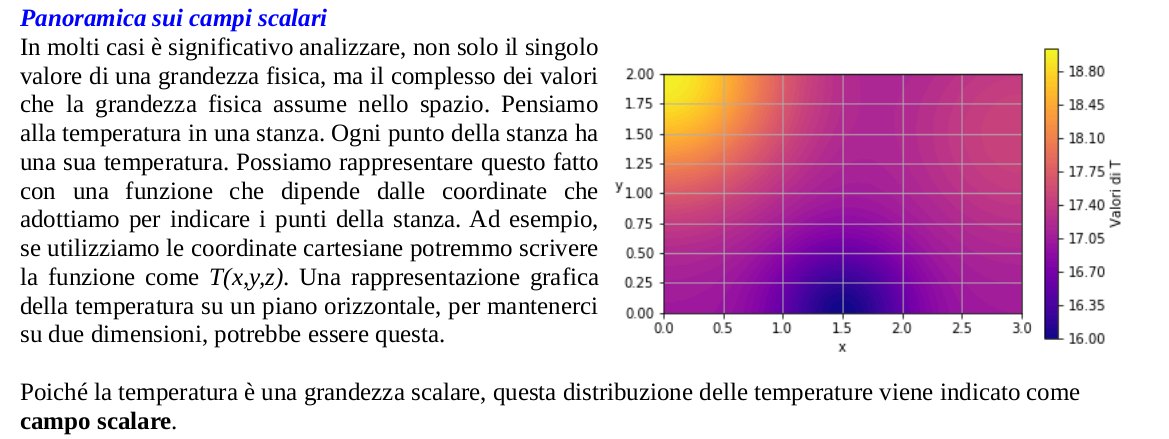
Il punto di partenza sono dagli oggetti di queste derivate. Vale a dire i campi scalari, vettoriali e tensoriali in generale. I campi associano i valori di una grandezza ai punti dello spazio.
Viene quindi naturale domandarsi quale sia il tasso di variazione di queste grandezze.
Le leggi della Relatività Generale concepita da Einstein sono espresse da relazioni tra tensori, vale a dire tra entità geometriche, valide in ogni sistema di coordinate. Il tasso di variazione che cerchiamo è una delle basi di questa costruzione. Anche esso dovrà essere un tensore che è denominato derivata covariante.
Per esplorare la relazione tra entità geometriche e le coordinate propongo un semplice esempio come il calcolo dell'angolo tra vettori. I vettori e l'angolo tra vettori sono entità geometriche. In particolare l'angolo è uno scalare. Il risultato del calcolo dovrà essere indipendente dalle coordinate. Dovrà essere lo stesso sia se effettuato in coordinate cartesiane sia se effettuato in coordinate polari.
Ritornando al tasso di variazione, partiamo dall'esplorazione dal caso più semplice. Il tasso di variazione di un campo di uno scalare. Vedremo che è un tensore che abbiamo già incontrato: il gradiente. Il gradiente è un tensore che si trasforma in modo covariante. Da qui il termine derivata covariante, in questo caso di un campo scalare. Per saggiare la sua natura tensoriale propongo il calcolo del tasso di variazione di un campo scalare lungo un vettore.
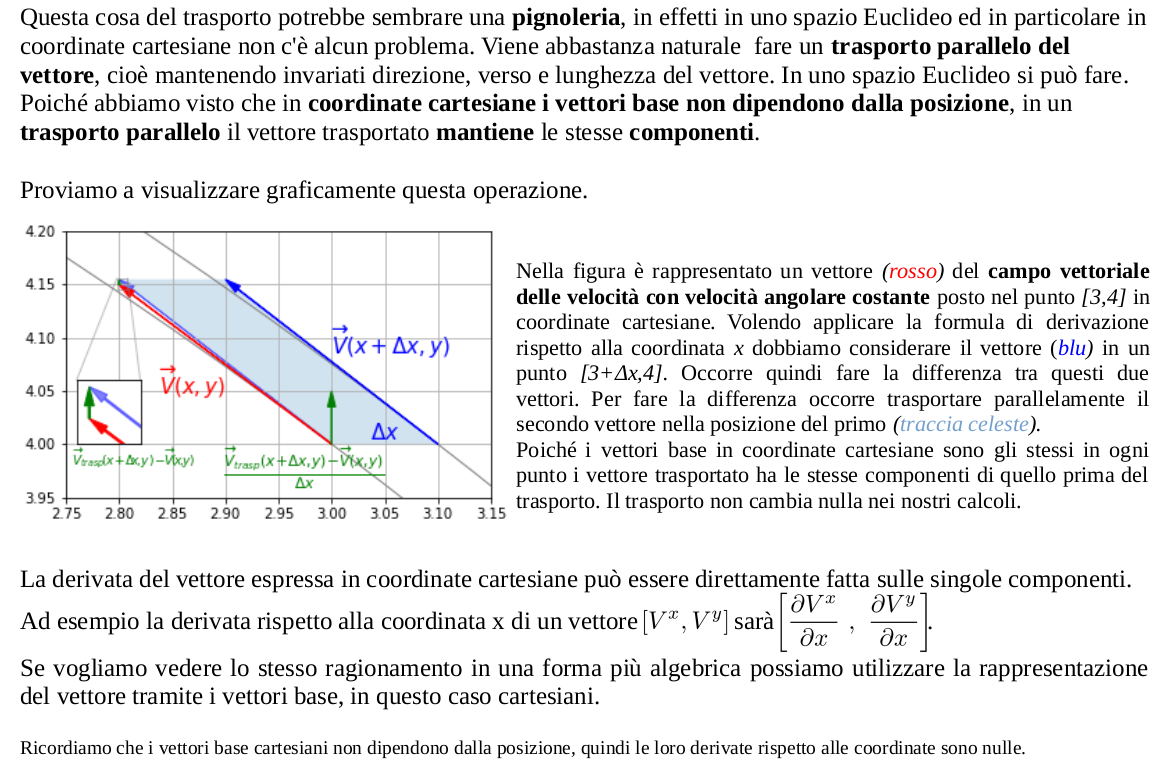
Passo quindi al tasso di variazione di un campo vettoriale. Prima in coordinate cartesiane e poi in coordinate polari. L'aspetto essenziale da affrontare è che per calcolare un tasso di variazione occorre confrontare due vettori posti in due punti diversi. Per fare il confronto occorre trasportare un vettore nel punto dove si trova l'altro vettore.
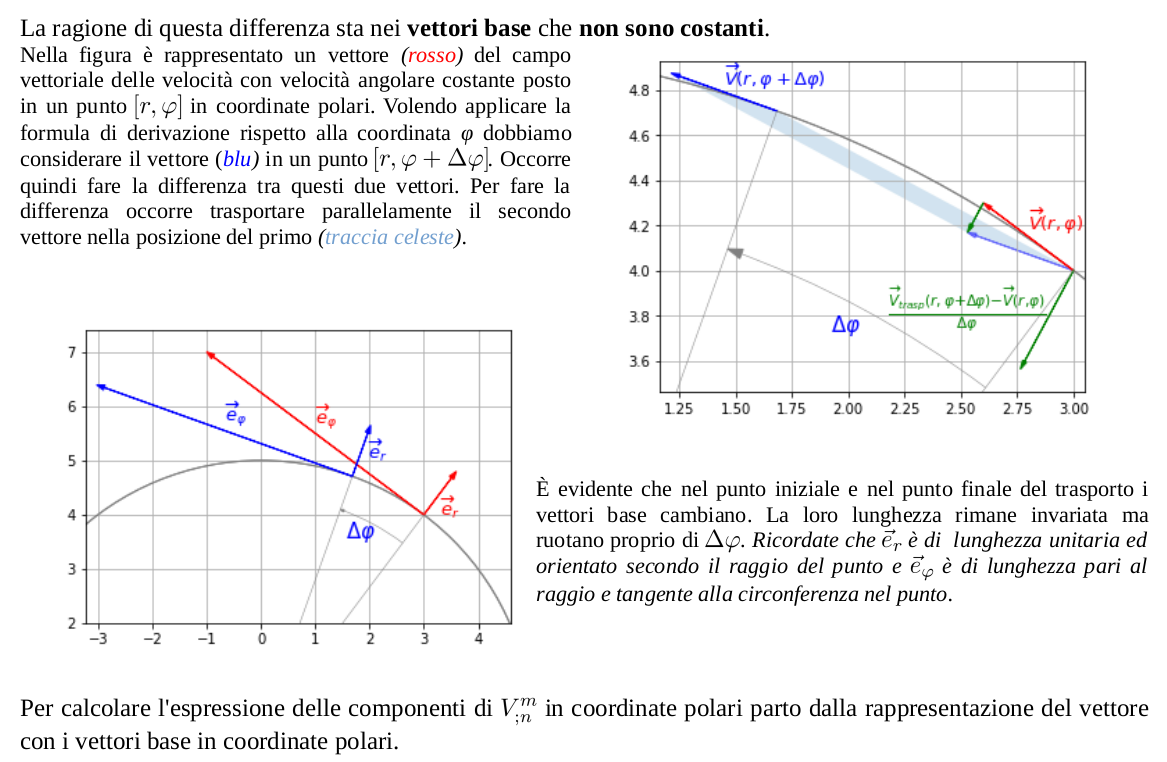
Nel caso di coordinate cartesiane, dove i vettori base sono costanti, ce la caviamo comunque con le derivate parziali delle componenti dei vettori. Le coordinate polari, per la loro caratteristica di essere curvilinee, fanno emergere la necessità di considerare anche le variazioni dei vettori base. Per esprimere le variazioni dei vettori base in una forma utilizzabile all'interno delle espressioni della derivata covariante si utilizzano dei particolari elementi denominati simboli di Christoffel. Con i simboli di Christoffel saremo in grado di esprimere le componenti del tensore derivata covariante di un vettore in una forma valida per le coordinate polari, applicabile ad ogni altro tipo di coordinate ed estendibile anche a spazi non Euclidei.
Aggiungo che questo articolo è una panoramica su questi argomenti con l'obiettivo dare una idea del loro contenuto. La trattazione non sarà rigorosa dal punto di vista matematico.
In fondo all'articolo ci sono gli sviluppi con i quali ho ottenuto le risposte alle domande.








Le trasformazioni covarianti e controvarianti dei tensori sono trattate in questo articolo.








 Abbiamo visto le loro espressioni nell'articolo precedente.
Abbiamo visto le loro espressioni nell'articolo precedente.


Qui di seguito gli sviluppi con i quali ho ottenuto le risposte alle domande.

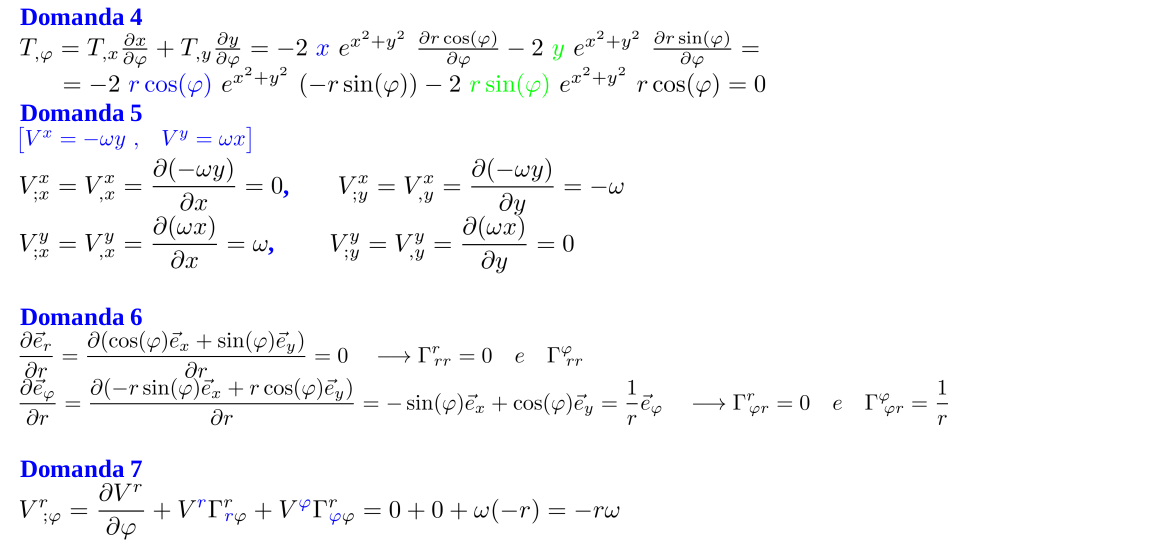






4 commenti
Devo ribadire il mio grazie e fare i più sinceri complimenti a Fabrizio. Sta dando un contributo essenziale all'intera faccenda, Direi, senza tema di smentita, che il lavoro più grande lo sta facendo lui! Quando uniremo gli articoli, avremo fatto una bella impresa a due teste e quattro mani!
Un dubbio mi costringe a soffermarmi sempre alla domanda 1 dell'articolo. La velocità V ha quale componente radiale zero e per componente trasversa la velocità angolare omega: ma quest'ultima non dovrebbe essere omega moltiplicata per il raggio r? Se non altro per omogeneità dimensionale con la componente radiale, in quanto questa certamente è misurata in m/s, mentre omega, velocità angolare, sarà certamente rad/s.
Sicuramente c'è qualcosa che mi sfugge, o qualche precedente riferimento che non ho letto. . .Vi sarei grato se voleste chiarirmi questo dubbio per seguire bene tutto il magnifico articolo. Grazie.
Raffaele
Commento modificato il 27/12/2021 ore 11:40
Raffaele,
ti ringrazio per la tua domanda. Mi fa molto piacere sapere che ci sono lettori che leggono in modo critico gli articoli e si fanno e fanno delle domande. Provo a risponderti.
Il fatto che in questo caso la seconda componente della velocità sia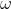 ,cioè
,cioè 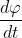 , dipende dalla scelta delle coordinate e dei vettori base con i quali stiamo operando che portano a componenti dei vettori spostamento dati da
, dipende dalla scelta delle coordinate e dei vettori base con i quali stiamo operando che portano a componenti dei vettori spostamento dati da ![[dr,d\varphi]](http://latex.codecogs.com/gif.latex?[dr,d\varphi])
Nella scelta delle coordinate e dei vettori base non c'è nessun vincolo riguardo l'omogeneità della grandezze, come in questo caso possono essere una lunghezza ed un angolo. Certamente è valida anche la scelta che porta alle componenti dei vettori spostamento che indichi implicitamente tu:![[dr,rd\varphi]](http://latex.codecogs.com/gif.latex?[dr,rd\varphi]) , ma non è una scelta obbligata.
, ma non è una scelta obbligata.
Le coordinate sono solo un segnaposto che può essere definito in modo ampiamente arbitrario. In questi articoli cerco di mettere in evidenza proprio questo per il ruolo che ha nella Relatività Generale.
Penso che la tua scelta sia collegata alla possibilità di definire in modo semplice la lunghezza del vettore velocità a partire dalle componanti del vettore. Lunghezza che, come indichi tu, è certamente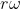 , in questo caso con r costante.
, in questo caso con r costante.
In questo modo si darebbe un diretto significato metrico alle coordinate ed alle componenti dei vettori. Significato che le coordinate, per come utilizzate nella Relatività Generale, non hanno.
Lo ha voluto mettere in evidenza lo stesso Albert Einstein in una intervista che ho citato nell’articolo precedente. Nello stesso articolo puoi trovare trattato in modo più ampio quanto ho esposto qui sopra ed il ruolo che ha il tensore metrico nella definizione della lunghezza di un vettore. C’è anche un breve appunto sulle ragione per le quali in RG non vengono utilizzati spesso vettori base che portano a componenti del tipo![[dr,rd\varphi]](http://latex.codecogs.com/gif.latex?[dr,rd\varphi]) .
.
Spero di averti dato gli elementi per sciogliere il tuo dubbio. Se così non fosse, le domande sono sempre benvenute.
Ho notato che nel commento precedente c'erano delle imprecisioni che ho provveduto a correggere.
Mi scuso con chi lo avesse letto nella versione precedente.