Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Riassumiamo in breve quello che abbiamo visto finora sulle curve ellittiche.

1. Sulle curve ellittiche definite da equazioni del tipo , è possibile definire una operazione di composizione interna. Se chiamiamo E l'insieme dei punti di una curva ellittica, tale operazione dunque è definita in:E x E--->E, e può essere interpretata in modo grafico in questo modo, pensando anche a tutti e tre i casi possibili

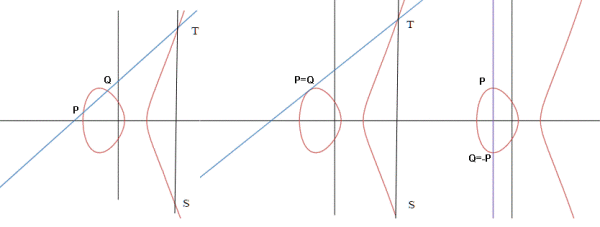
Si considerano due punti P,Q sulla curva; Si traccia la retta per i due punti, che nel caso i due punti siano coincidenti diventa la tangente;si trova la terza intersezione T e poi si traccia la verticale passante per T trovando così S; P+Q=S. T esiste sempre come abbiamo visto nel quiz; il caso limite, quando P e Q stanno su una retta verticale, lo abbiamo studiato in coordinate proiettive; in tal caso la retta per P e Q interseca la curva all'infinito, il punto improprio . Estendendo quindi E aggiungendo  si ottiene proprio un insieme con una legge di composizione interna. Per dire che E è un gruppo dobbiamo provare che :

L'operazione è associativa, commutativa,  esiste un elemento neutro e  per ogni elemento abbiamo un opposto. Che l'operazione sia commutativa discende dalla definizione; scambiando P con Q otteniamo come P+Q sempre S e nel caso verticale sempre . Per quanto riguarda l'associatività darò un accenno in appendice ad una sua giustificazione. Chi sarà l'elemento neutro? Cerchiamo un  elemento N tale che P+N=P qualsiasi sia P (basta questo, essendo commutativa, P+N=N+P). Proviamo che N=.

Se facciamo infatti P+, dobbiamo considerare la retta  passante per P e , che interseca appunto la curva in  (all'infinito).

Quindi P+=P.  Notiamo poi che se consideriamo i punti P e Q sulla verticale, ovvero con Xp=Xq, P+Q=. Infatti la verticale interseca la curva in . Quindi P+Q=; questo significa che Q=-P. Quindi abbiamo trovato anche l'opposto di un punto P. In definitiva, la curva con l'operazione così definita è proprio un gruppo.

Gli algoritmi di calcolo; punti distinti

Nel  quiz abbiamo calcolato anche il procedimento per il primo caso, quello di due punti distinti.

Indicando con (x1,y1) le coordinate di P, (x2,y2) le coordinate di Q, e con (x3,y3) le coordinate di P+Q=S,

in definitiva si aveva:

Punti coincidenti

Nell'ultimo articolo avevamo calcolato il coefficiente m nel caso di tangenza, ovvero di due punti coincidenti:

Basta sostituire ad m il suo valore valore per ottenere S nel caso di tangenza, ovvero di P=Q:, e tener conto che x1=x2,y1=y2

 

.

Notare che se sappiamo fare P+P, sappiamo fare anche P+P+P, P+P+P+P,..ecc.

In generale sappiamo quindi fare nP=P+P+....P n volte

Punti su retta verticale

Nel caso verticale, ovviamente x1=x2; ne segue che :

essendo x1=x2:

essendo y1<>y2 ne segue y1=-y2, quindi l'opposto di (x1,y1) è (x1,-y1).

Naturalmente questi algoritmi, che non implicano nessun ragionamento, possono essere eseguiti anche da un computer.

Abbiamo dunque concluso che l'insieme dei punti di una curva ellittica con il punto improprio come zero costituisce un gruppo vero e proprio. Finora abbiamo considerato le curve con infiniti punti, definite cioè sui numeri reali. La prossima volta vedremo come fare le stesse operazioni su un campo finito, tipo Zp (interi modulo p con p primo). Sarà una cosa molto interessante e divertente, e ci porterà verso la crittografia moderna.

 

Appendice: giustificazione intuitiva della proprietà associativa.

La dimostrazione formale della proprietà associativa, comporta delle tecniche riguardanti le soluzioni di equazioni polinomiali molto avanzate. Tuttavia, volevo dare solo una giustificazione grafica di tale proprietà; si tratta di trovare graficamente (P+Q)+R, P +(Q+R), e poi verificare che sono uguali ad un certo punto, chiamiamolo N.

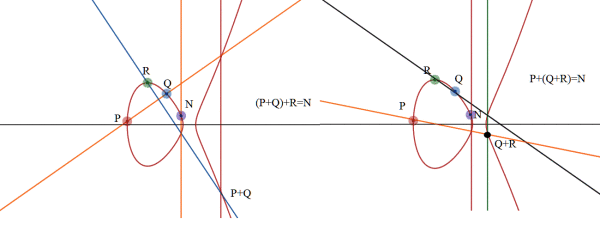
Nello schema sono rappresentati i due modi diversi per calcolare la somma di tre punti;in entrambi i casi si vede che coincidono con il punto N. Questa non è chiaramente non è una dimostrazione valida. Chi vuole può provare a disegnarne altri casi, (io ho usato desmos) . Chi ancora non è soddisfatto può provare ad usare le due formule:

 

applicandole alle due somme fatte in ordine diverso, e vedere se coincidono. Confesso che non ho provato, ma immagino che vengano fuori dei conti brutali. Se qualcuno lo fa mi avvisi, così lo aggiungiamo all'articolo.